積分の新しい景色へ──単関数から見るルベーグ積分(ルベーグ積分のはじまり①)
前回の記事では、「リーマン積分ではなぜ不十分なのか?」という疑問から出発して、ルベーグ積分がどのような発想で登場してきたのかを紹介しました。
リーマン積分は横に切る。ルベーグ積分は縦に見る。
そんな視点の違いが、積分という操作の本質を捉え直すヒントになりました。
まだ前回を読んでいない方は、以下の記事を先に読むと、今回の内容がよりスムーズに理解できます:
今回からは、ルベーグ積分を「実際にどう定義していくのか?」2回構成で解説していきます。
その前半として今回は"単関数"という特殊な関数で定義していきます。
「単関数って何?」「なぜ積分の定義はそこから始まるの?」
そんな疑問を持っている方はぜひ目を通してください。
なぜ“単関数”から始めるのか?
ルベーグ積分は、「関数の値をとっている“範囲”の大きさに重みをつけて足し合わせる」ことで面積を測るという、新しい積分の考え方でした。
でもいきなり一般の関数を扱おうとすると、どうしても抽象的になってしまって、直感的にイメージしづらくなります。
そこで、最初に出てくるのが 単関数(simple function) という、ものすごく扱いやすい関数です。
単関数とは?
可測空間
-
(a_i \geq 0) -
(E_i \in \mathcal{F}) -
(1_{E_i}(x)) x \in E_i
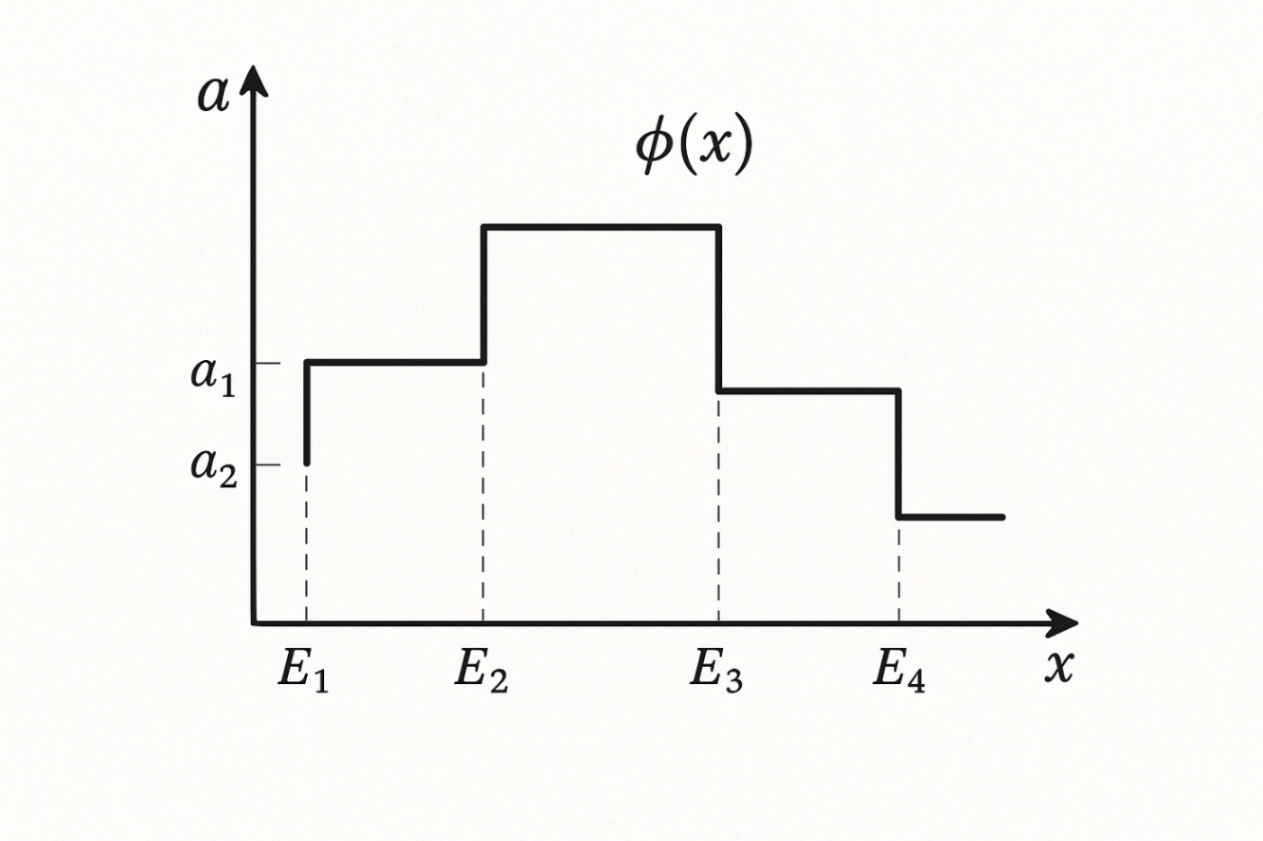
図1:単関数は有限個の高さブロックでできた関数
つまり、有限個の値をとる、段差のような関数です。
積分の“最小単位”を考えてみる
「この区間では3、この区間では5…」といった段差構造の関数があったとします。
このとき、各ブロックについて「高さ × 幅(測度)」を計算して合計すれば、面積が求まります。
つまり、まさに:
高さ × 横の広さ の足し算
という発想が自然に出てくるのが、単関数です。
単関数の積分を考えてみよう
単関数は、高さが一定のブロックのような関数でした。
このような関数の積分はとても素直に定義できます。
それぞれの“高さ”に、その高さをとっている部分集合の“面積”を掛けて、すべて足し合わせるだけです。
積分の定義
単関数
ここで:
-
a_i -
E_i -
\mu(E_i)
直感的な意味
この式はまさに:
高さ × 面積 を足し合わせたもの
になっています。
- 「この範囲では高さ3」→ 高さ3 × 面積
- 「この範囲では高さ5」→ 高さ5 × 面積
- 「この範囲では高さ1」→ 高さ1 × 面積
→ 全部合計すれば、関数の“塗りつぶした面積”が得られる
まるで色ごとに区分されたグラフの面積を「色別に合計」していくような感じです。
例(イメージ)
例えば、以下のような関数を考えてみましょう:
- 区間
[0,1),(4,5] - 区間
[1,3) - 区間
[3,4]
そのとき積分は:
まさに、**高さごとの“面積の足し算”**という感じがすると思います。
軽く触れる「単関数近似」の入口
ここまでで「単関数」を使ったルベーグ積分の“最小単位”が理解できました。
しかし、現実にはもっと複雑な関数を積分したい場面がほとんどです。
そこで次回は、任意の非負可測関数を「単関数の列」で下から近づける方法――
いわゆる 単関数近似 を使って、どのようにルベーグ積分の定義を拡張するのかを見ていきます。
「単関数の積分を積み重ねることで、イメージどおりに一般の関数も測れる」
この強力な発想を、視覚的なステップとともにじっくり掘り下げます!
ここまで読んでいただき、ありがとうございます。
参考になりましたらいいねやフォローをしていただけると嬉しいです!
次回もお楽しみに!
Discussion