🙌

ABC191 D - Circle Lattice Points

2021/02/14に公開

競技プログラミング

tech

問題概要

中心 $(X, Y)$ 、半径 $R$ の円の内部および円周上にある格子点の数を求めよ

解法

求める格子点を $(x, y)$ とおく
まず $x$ として考えられる範囲を求める
$x$ は円の中心から $R$ の距離の範囲にあるので、

$X - R \le x \le X + R$

$x$ は整数であるので

$\lfloor X - R \rfloor \le x \le \lceil X + R \rceil$

そして、 $x$ が決まれば $y$ の範囲も決まる

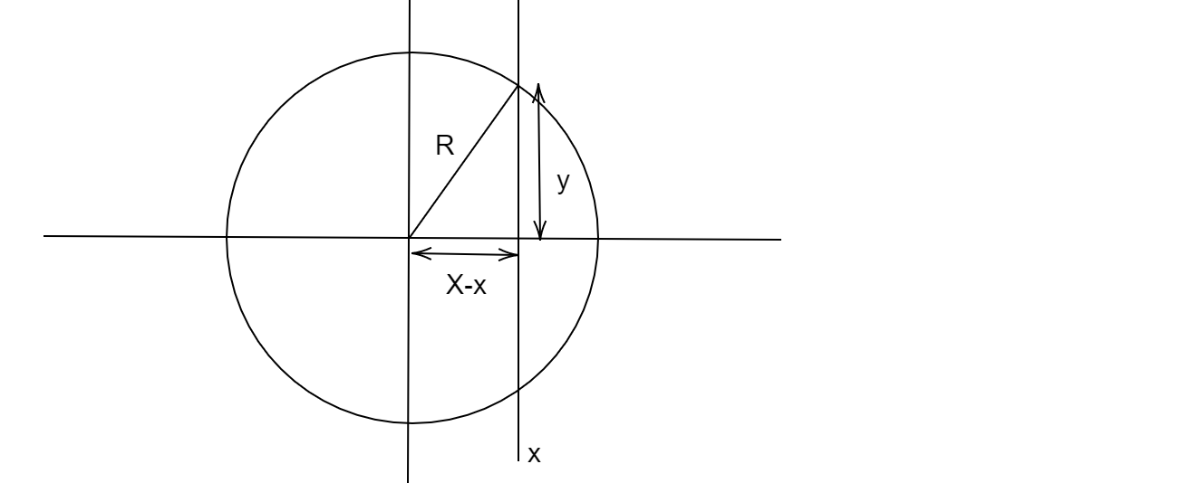
上図において、三平方の定理より

R^2 = (X-x)^2 + y^2 \tag{1}

が成り立ち、これから $y$ の範囲を決めることができる

この問題では、 $X, Y, R$ が小数点以下4桁までの小数として与えられており、
愚直に計算すると誤差が問題になる
まず $X, Y, R$ を1000倍して、整数にする
この計算においても受け取った数を浮動小数点数として表す際の誤差、
1000倍する際の誤差が問題になるため注意する必要がある
roundなどを使って丸めることで誤差の影響を無視することができる

求める格子点の個数は中心 $(1000X, 1000Y)$ 、半径 $1000R$ の円の内部および円周上にある、 $(x, y)$ が共に1000の倍数であるような点の個数に等しい
まず $x$ の範囲を求める
$x = 1000i$ と置くと

1000X - 1000R \le 1000i \le 1000x + 1000R

\lfloor \frac{1000X - 1000R}{1000} \rfloor \le i \le \lceil \frac{1000X + 1000R}{1000} \rceil

そして $y$ の範囲を決めるときにそのまま(1)式から

y = \sqrt{R^2 - (X-x)^2}

としてしまうと、平方根の計算で浮動小数点数が出てきてしまう
(1)式に対して、

R^2 \ge (X-x)^2 + y^2

という条件を考えると、これは単調性をもち、
二分探索によって、この条件をみたす最大の整数 $y$ を求める事ができる
その整数値を $y'$ とすると、 $-y'$ 以上、 $y'$ 以下の1000の倍数の個数が答えになる
$y = 1000j$ とすると

-y' \le 1000j \le y'

\lfloor \frac{-y'}{1000} \rfloor \le j \le \lceil \frac{y'}{1000} \rceil

つまり $\lceil \frac{y'}{1000} \rceil - \lfloor \frac{-y'}{1000} \rfloor + 1$ 個存在する
各 $i$ について、この個数を答えに加算していく

ABC191 D - Circle Lattice Points

問題概要

解法

提出コード

Discussion