見たら「ん？」となるエラーバーのグラフ

はじめに

実験や数値計算などでエラーバーがついているグラフをよく使いますが、見ていると「ん？」となるグラフをよく見かけます。いくつか例を挙げて見ましょう。

ケース1

例えばこんなグラフがあったとします。

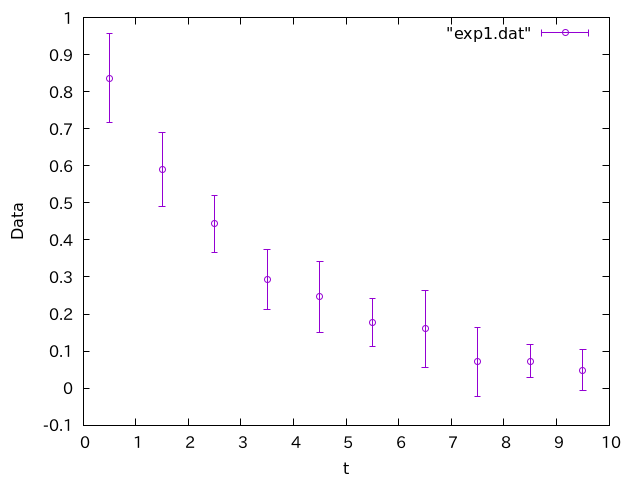
何かが時間に対して指数関数的に減衰していることを表しているようです。僕は発表でこういうグラフを見かけたら「ん？」と思います。

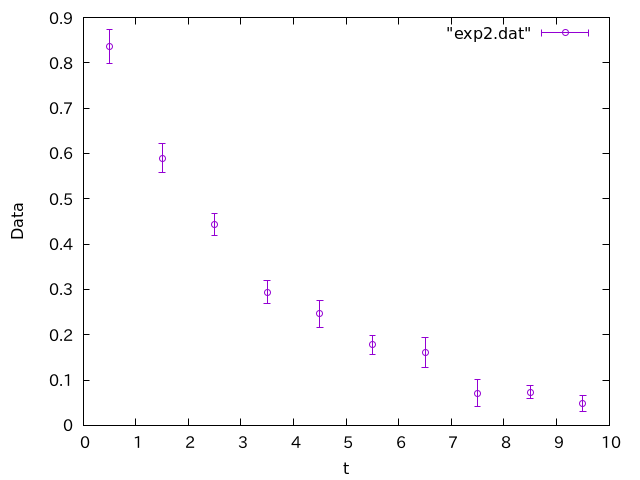
一方こちらのグラフは、少なくともエラーバーの付き方はまともです。

ケース2

もし、観測値のそれぞれに独立なノイズが乗っているのであれば、エラーバーは、観測回数を増やせば減っていくはずです。観測回数$n$に対して、物理量の推定値とエラーバーがどうなるかを表したグラフでこんなものがあったとします。

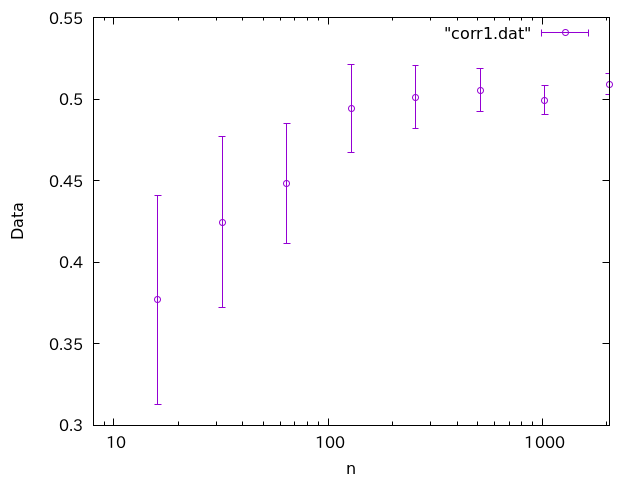
試行回数$n$を増やすにつれて、平均値は$0.5$に収束し、さらにエラーバーも小さくなっています。一見それっぽく見えますが、僕はこのグラフを見たら「ん？」と思います。

一方、こちらも同様なグラフです。

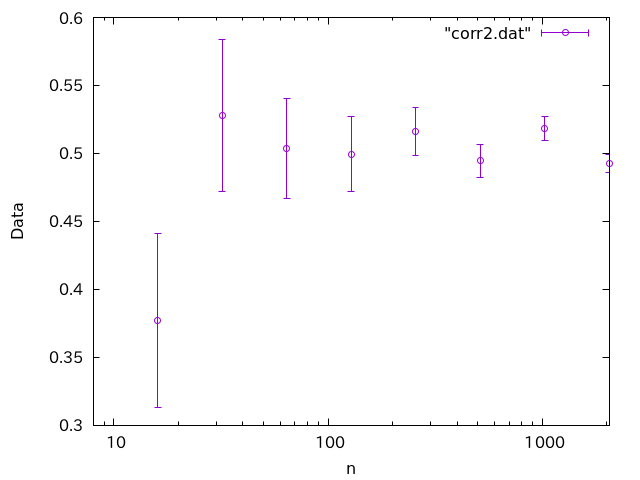
試行回数$n$を増やすにつれて、平均値は$0.5$に収束し、さらにエラーバーも小さくなっているのは先程と同じですが、こちらはまっとうなグラフに見えます。

ケース3

シミュレーションでは、時系列を追うことがあります。例えば生データとしてこんなのが得られたとしましょう。

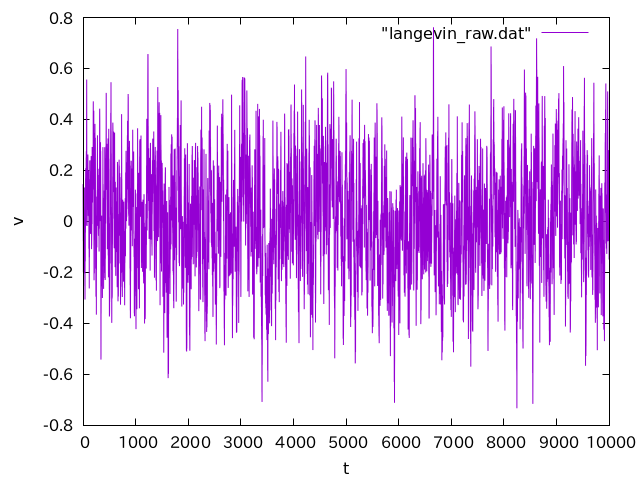
これじゃわけがわからないので、一定区間ごとに区切って平均を取ります。ついでにエラーバーもつけましょう。

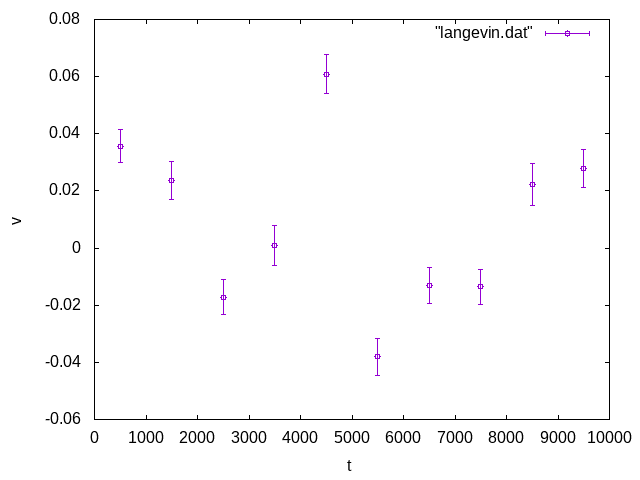
慣れている人が見れば、このエラーバーはおかしいと思うでしょう。しかし、エラーバーに詳しく無い人はこのままのグラフを使ってしまいがちです。

以下は「ある処理」をしたデータに対して、同様な解析をしたものです。

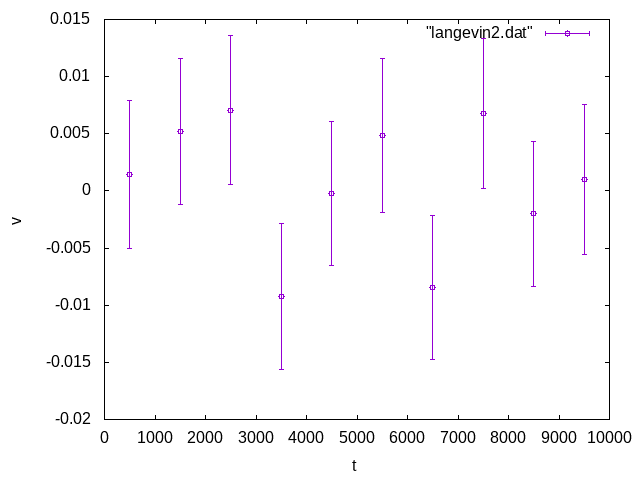
こちらはエラーバーがまともです。

これら３つのケースについて、すぐに「おかしい」と思ったでしょうか？以下、それぞれのケースについて何がおかしいかを説明してみます。

ケース1：エラーバーが大きすぎる

多くの場合、エラーバーは「観測の度に独立なノイズが乗る」ということを仮定してつけます。独立なノイズを何度も観測して平均すると、それはガウス分布に近づきます。そこで、ノイズがガウス分布であると仮定した時に、「観測値の推定値にどれくらい誤差があるか」を推定したものがエラーバーです。平均$\mu$、分散$\sigma^2$のガウス分布は以下のように表現されます。

$$f(x) = \frac{1}{\sqrt{2\pi \sigma^2}} \exp\left(-\frac{(x-\mu)^2}{2 \sigma^2} \right)$$

いくつか流儀がありますが、エラーバーとして$\sigma$の値を取ることが多いです。これを「1シグマ」と呼びます。無限回の観測を行った場合の平均値の期待値を、便宜上「真の値」^[1]と呼ぶことにすると、大雑把にいえば「平均値の推測値の両側1シグマの範囲に、真の値が含まれる確率が68%くらいかな？」と思うのが「1シグマのエラーバー」の意味となります。

さて、エラーバーの範囲に「真の値」を含む確率が68%なのですから、逆に言えば3回に一度は「真の値」はエラーバーの範囲外にあるはずです。それを踏まえて、先程のケース1のグラフをもう一度見てみましょう。

なんとなく指数関数的な減衰が見えますね。ありそうな指数関数を重ねてみましょう。

この線は、「この計算の精度を高くしていったら、データはこの線に収束する」と期待される線です。これを見ると、全てのデータ点について、この線にエラーバーがかかってしまっています。3つに1つは外れないとおかしいのですから、このエラーバーは明らかに大きすぎです。

このグラフのデータは以下のコードで作られています。

import numpy as np

N = 10
np.random.seed(1)
for i in range(10):
    x = i + 0.5
    d = np.zeros(N)
    d += np.exp(-x/3)
    d += np.random.randn(N)*0.1
    y = np.average(d)
    e = np.std(d)  # <- 母標準偏差を求めている
    print(f"{x} {y} {e}")

指数関数$\exp(-x/3)$に対して、ノイズが乗ったようなデータです。それを各$x$について平均と標準偏差を求めていますが、標準偏差にnumpy.stdを使っています。numpy.stdは母標準偏差を返しますが、我々がプロットしたいのは「平均値の推定誤差」であり、さらにデータ数$N$の平方根$\sqrt{N}$で割ってやる必要があります。修正しましょう。

import numpy as np

N = 10
np.random.seed(1)
for i in range(10):
    x = i + 0.5
    d = np.zeros(N)
    d += np.exp(-x/3)
    d += np.random.randn(N)*0.1
    y = np.average(d)
    e = np.std(d)/np.sqrt(N)  # √Nで割った
    print(f"{x} {y} {e}")

こうして作られたグラフはこうなります。

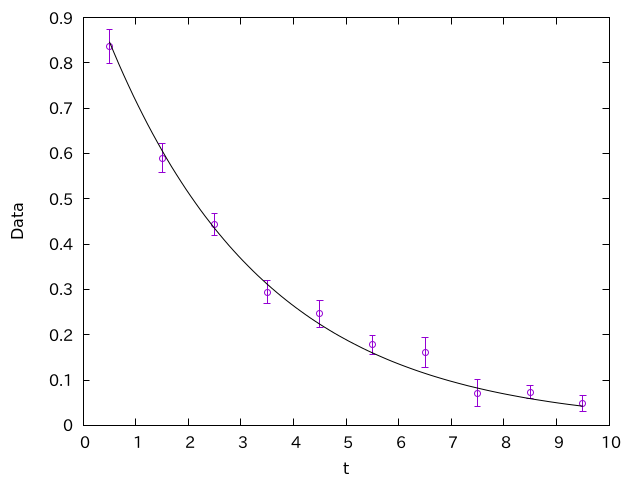
実線に対して、エラーバーが重ならない点がでてきました。こちらはまっとうなデータに見えます。

一般に、データはエラーバーくらいの振幅で揺らぐはずです。ところが、データの平均値が非常にきれいな振る舞いをしているにも関わらず、エラーバーが大きすぎる場合、何かがおかしいです。よくあるパターンの一つは、このように$\sqrt{N}$での割り忘れですが、他にも観測データに振動が乗っていたりするとエラーバーが大きくなってしまいます。

いずれにせよ、「なんとなくデータが乗ってそうな曲線」に対して、「エラーバーが重なる確率は68%くらい」と思っておくと、変なグラフにすぐに気がつくと思います。

ケース2：データが片側に偏っている

観測回数を増やすほど、期待値が0.5に近づくような観測データがあるとします。観測回数を増やすほど、エラーバーは小さくなるはずです。

観測回数$n$に対して、期待値とエラーバーがどうなるかを見たのが以下のグラフです。

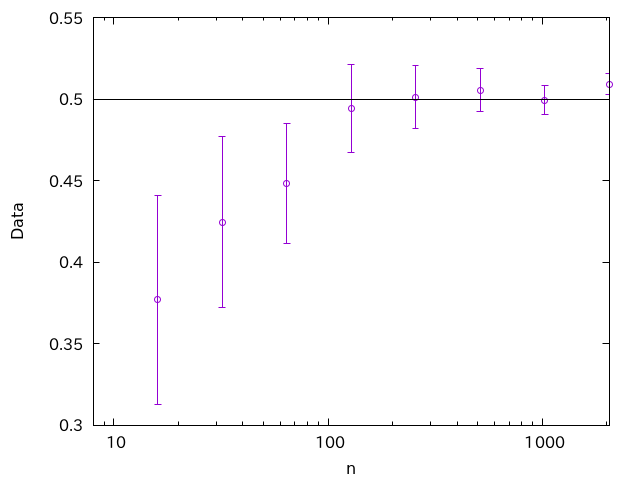
確かに試行回数を増やすと平均値は0.5に収束し、さらにエラーバーも小さくなっていくのが見ます。しかし、こんなグラフを見たら「ん？」と思わなくてはいけません。

もしそれぞれのデータが独立であるならば、「真の値」である「0.5」の両側に均等にばらつくはずです。ところが、最初に連続して4回、下側にブレています。どちらにブレるかは1/2なので、4回下にいくのは確率16分の1と、決してありえない確率ではありませんが、グラフを見ると、明らかに右のデータが左側のデータに「引きづられて」います。これは、各データ点が独立でないことを強く示唆します。

実際、左側のデータを含んだ形で右側のデータが計算されています。こちらがソースです。

import numpy as np

np.random.seed(1)

N = 2048
d = np.random.random(N)
for i in range(4, 12):
    n = 2**i
    dd = d[:n]
    ave = np.average(dd)
    err = np.std(dd)/np.sqrt(n)
    print(f"{n} {ave} {err}")

最初に2048個のデータを作り、それを最初の8個、最初の16個、最初の32個・・・とデータ数を増やして平均と誤差を計算しています。16個のデータの平均を計算するとき、先程の8個のデータを含んでいるため、これらは強く相関します。これにより、8個のデータがたまたま下側にずれたことを引きずります。片側に連続してずれたのはこのためです。

最初の8個、次の16個...を完全に異なるデータにすると、このようなことは起きません。

import numpy as np

np.random.seed(1)

N = 2048
for i in range(4, 12):
    n = 2**i
    dd = np.random.random(n)
    ave = np.average(dd)
    err = np.std(dd)/np.sqrt(n)
    print(f"{n} {ave} {err}")

こちらは、データセット毎に全く新たに乱数を作っているため、異なるデータセット間で相関はありません。すると、こんなグラフになります。

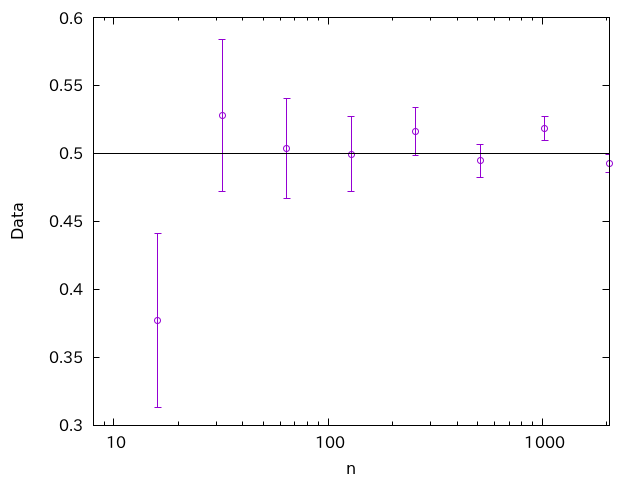
0.5の周りに均等にバラけているのがわかります。

ケース3：エラーバーが小さすぎる

1シグマのエラーバーを採用した場合、「真の値」を含む確率が68%です。さて、2シグマを取る、つまりエラーバーの長さを倍にすると、その中に含まれる確率は95%に、3シグマなら99.7%になります。

つまり、1シグマのエラーバーならそこそこ外れる確率はある(3点に1点)けれど、エラーバーの幅の三倍外れる確率は極めて低い(1000点に3点)ことになります。

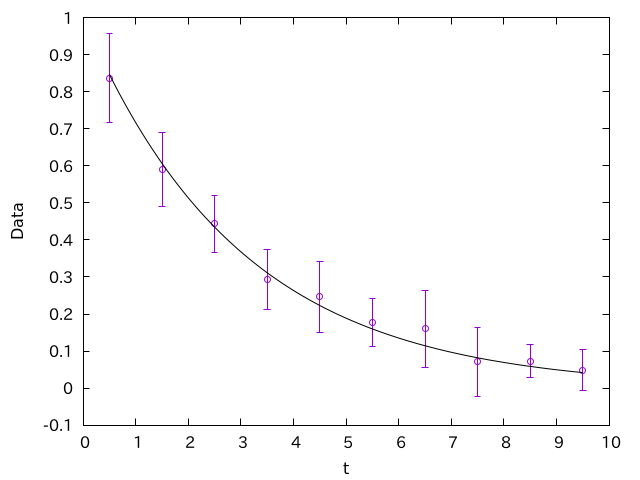
それを踏まえて以下のグラフを見てみましょう。

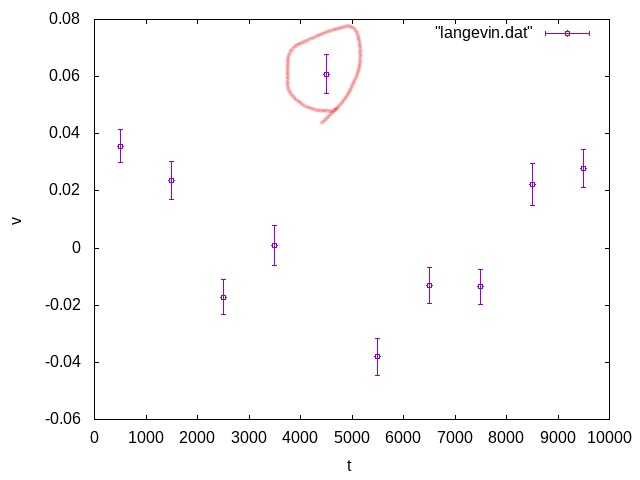
よほど複雑な振る舞いをする関数でなければ、平均0の周りに揺らぐデータのように見えます。ところが、丸で囲んだデータは、エラーバーの幅の10倍近く外れています。5倍外れる確率が0.000057%ですから、少なくともこれは「独立なノイズによる誤差」と思ってはいけないことになります。

実はこのグラフは以下のLangevin方程式の時系列から得られたものでした。

import numpy as np

N = 1000
v = 0.0
gamma = 0.1
np.random.seed(1)

for j in range(10):
    d = np.zeros(N)
    for i in range(N):
        v += np.random.randn()*0.1
        v -= gamma * v
        d[i] = v
    ave = np.average(d)
    err = np.std(d) / np.sqrt(N)
    print(f"{(j+0.5)*N} {ave} {err}")

これは、水の中にあるコロイド粒子の速度をシミュレーションしたもので、抵抗による速度の減衰と、水分子によるランダムな衝突を計算しています。すると、あるステップの速度と、次のステップでの速度には強い相関があることになります。つまり、ある時刻でコロイド粒子が右に向かって進んでいる場合、非常に短い時間だけ進んだ後も、やはり右に進んでいる確率が高いことになります。このように、データ間に強い相関がある場合、そのまま誤差を推定するとエラーバーを過小評価します。

Langevin系では、緩和の時定数$\gamma$の逆数程度の時間だけ相関が続きます、いま$\gamma = 0.1$なので、100ステップも取れば相関は概ね切れていることが期待されます。そこで、100回に一度観測することにして、得られた時系列に同じ解析をしてみましょう。

import numpy as np

N = 1000
v = 0.0
gamma = 0.1
np.random.seed(1)

for j in range(10):
    d = np.zeros(N)
    for i in range(N):
        for _ in range(100): # 100回に一度観測
            v += np.random.randn()*0.1
            v -= gamma * v
        d[i] = v
    ave = np.average(d)
    err = np.std(d) / np.sqrt(N)
    print(f"{(j+0.5)*N} {ave} {err}")

こうして得られたのが以下の図です。

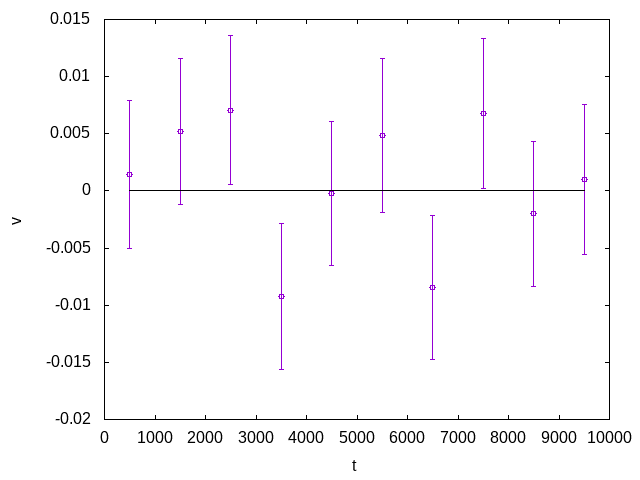
平均値である0の周りにデータ点が揺らいでおり、かつ、たまにエラーバーが0にかからない奴がいて、さらにエラーバーに対して「離れすぎているデータ」もいない、という、「まとも」なグラフになっています。

まとめ

エラーバーを含むグラフを見たときに「ん？」と思うケースをまとめてみました。エラーバーは「観測値に独立なノイズが乗ると仮定した場合、観測値の推定値の推定誤差」を表します。エラーバーを1シグマでとった場合、エラーバーの範囲に「真の値」が含まれる確率は68%、エラーバーの二倍の範囲に含まれる確率は95%、三倍なら99.7%です。したがって、なんとなくデータが乗りそうな曲線を「真の曲線」と呼ぶと

• 3つに1つは「真の曲線」にエラーバーがかからないデータが存在する
• データ点は「真の曲線」の両側に均等にばらつく
• エラーバーの数倍離れるようなデータ点の出現確率は極めて低い

とい性質を持ちます。逆に言えば、

• すべての点においてエラーバーの範囲内に「真の曲線」があるように見える(ケース1)
• 明らかにデータ点が「真の曲線」の片側に偏っている(ケース2)
• 「真の曲線」からエラーバーの数倍以上離れたデータ点が存在する(ケース3)

を見たら、「何かがおかしい」ことになります。

ありがちなのは、$\sqrt{N}$で割忘れている、データ点に相関がある(高周波振動を持つ場合もこれ)、系に系統誤差があるなどですが、大事なのは、まず「おかしい」と思うことです。「おかしい」と思わなければ原因を究明しようとも思わないわけですから。

本稿が「おかしなエラーバーのグラフ」を減らす手助けになれば幸いです。

参考文献

• この記事は以前Qiitaに書いたものをリファインしたものです。
• Jackknife法とサンプル数バイアス サンプル数に対してバイアスが乗る場合、それをどのように消すかという話。

脚注

1. 一般には「真の値」はわからないので、「真の値」という呼び方は良くない気がしますが、便宜上こう呼ぶことにします。