三種類の音律を聴き比べる
はじめに
Pythonで音を鳴らすという記事で、平均律とピタゴラス音律について触れました。音律とは、いわゆる「ドレミファソラシド」を、どのような周波数比とするかの決まりです。
よく使われる音律に「ピタゴラス音律」「純正律」「平均律」があります。せっかく自由に音を作れるようになったので、それを聴き比べて見ましょう。
ソースコードは以下においてあります。
Google Colabで開いてそのまま試すこともできます。
三種類の音律
ピタゴラス音律
ピタゴラス音律は、「2:3」の比にこだわった音律です。音は、周波数が整数比だときれいに響きます。そこで、周波数が二倍の音を「1オクターブ上の音」と呼びましょう。逆に周波数を半分にすると1オクターブ下がります。この1オクターブを8個の音に分け、「ドレミファソラシド」と名前をつけます。以下、「ドレミファソラシド」をCDEFGABCで表現します。
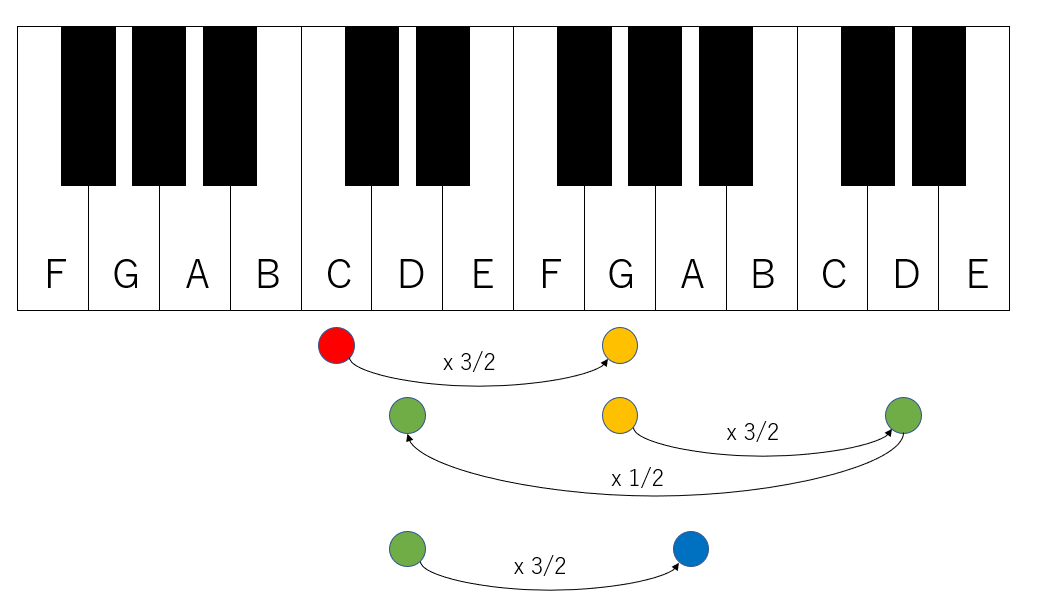
まず、ド(C)を基準にしましょう。この周波数を3/2倍した音を「ソ(G)」と呼びます。ソはドから4つ全音上げた音です(完全5度と呼びます)。
次に、ソ(G)から4つ全音上げた音をレ(D)と呼びましょう。周波数は基準音の9/4となりますが、これを1オクターブ下げます。すると周波数が半分となるので、基準音の9/8倍となります。
こうして、完全5度上げて、もしオクターブを超えたら周波数を半分にする、ということを繰り返すことで、Cから順にソ(G)、レ(D)、ラ(A)、ミ(E)、シ(B)が決まります。
逆に、Cから完全5度下げて(周波数を2/3して)、オクターブの修正をする(周波数を倍にする)ことでファ(F)が決まります。
同様な手順で半音も作ることができますが、ここでは全音だけ、ドレミファソラシドの8音の比だけ考えましょう。コードに落とすとこんな感じになるでしょう。
ratio_p = [1] * 8
ratio_p[7] = ratio_p[0] * 2 # C->C
ratio_p[4] = ratio_p[0] * Fraction(3, 2) # C->G
ratio_p[1] = ratio_p[4] * Fraction(3, 2) / 2 # G->D
ratio_p[5] = ratio_p[1] * Fraction(3, 2) # D->A
ratio_p[2] = ratio_p[5] * Fraction(3, 2) / 2 # A->E
ratio_p[6] = ratio_p[2] * Fraction(3, 2) # E->B
ratio_p[3] = ratio_p[0] * Fraction(2, 3) * 2 # C->F
for n, r in zip(list("CDEFGABC"), ratio_p):
print(f"{n}: {r}")
音を作るとき完全五度であることを反映して、もとの音と作る音のインデックスに「7を法として4の差がある」ことに注意しましょう。i+4 mod 7で、7をはみ出した時に2で割ったりかけたりしています。
実行結果はこんな感じです。
C: 1
D: 9/8
E: 81/64
F: 4/3
G: 3/2
A: 27/16
B: 243/128
C: 2
純正律
ピタゴラス音律では、周波数比3:2だけを使って音を作っていきましたが、純正律では4:5:6の比を使います。
- まず、ド(C)を基準にして、「ドミソ(CEG)」が4:5:6となるように周波数比を決めます。
- 次にソ(G)を基準として、「ソシレ(GBD)」が4:5:6となるように周波数比を決めます。
- 最後はド(C)を一番上の和音として「ファラド(FAC)」が4:5:6となるように周波数比を決めます。
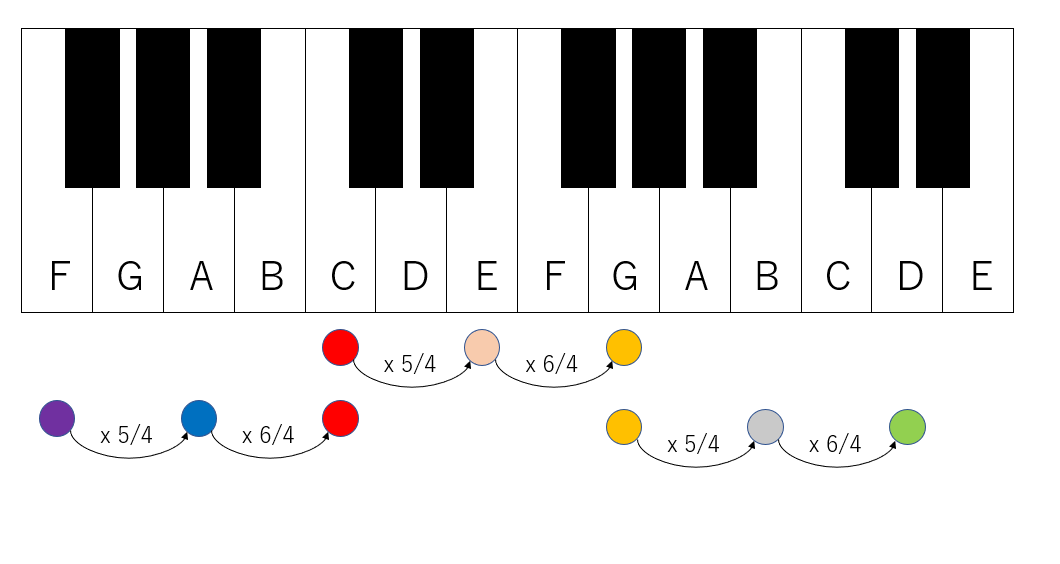
こうして、全ての音が決めることができます。コードに落とすとこんな感じになるでしょう。
ratio_j = [1] * 8
ratio_j[7] = ratio_j[0] * 2 # C->C
# C:E:G = 4:5:6
ratio_j[2] = ratio_j[0] * Fraction(5, 4)
ratio_j[4] = ratio_j[0] * Fraction(6, 4)
# G:B:D = 4:5:6
ratio_j[6] = ratio_j[4] * Fraction(5, 4)
ratio_j[1] = ratio_j[4] * Fraction(6, 4) / 2
# F:A:C = 4:5:6
ratio_j[3] = ratio_j[0] * Fraction(4, 6) * 2
ratio_j[5] = ratio_j[0] * Fraction(5, 6) * 2
for n, r in zip(list("CDEFGABC"), ratio_j):
print(f"{n}: {r}")
ピタゴラス音律がインデックスを4ズレで作っていたのに対して、「0,2,4」、「4,6,1」、「3,5,0」と、純正律は2ズレで音を作っているのがわかると思います。
実行結果はこうなります。
C: 1
D: 9/8
E: 5/4
F: 4/3
G: 3/2
A: 5/3
B: 15/8
C: 2
平均律
ピタゴラス音律が2:3、純正律が3:4:5という整数比にこだわって作った音であるのに対して、1オクターブを単純に対数スケールで12等分するのが平均律です。どの和音もかならずうなりが出てしまうというデメリットはありますが、連続する音の比が全て等しくなるので転調が容易になるというメリットもあります。平均率では、1オクターブを対数スケールで12等分するので、全音上がる時には周波数が
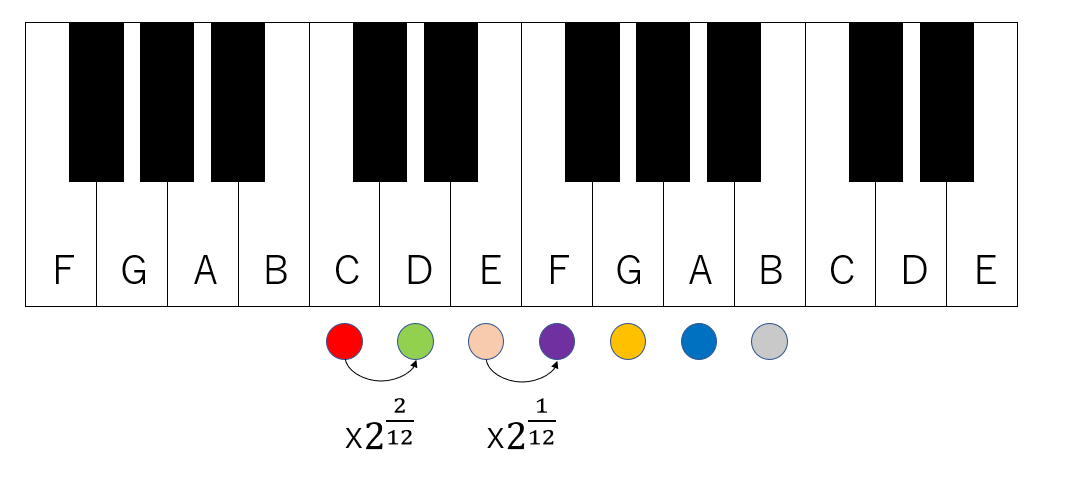
今回は全音だけ扱うので、コードに落とすとこんな感じでしょうか。
n = [0, 2, 4, 5, 7, 9, 11, 12]
ratio_e = [2**(i/12.0) for i in n]
for n, r in zip(list("CDEFGABC"), ratio_e):
print(f"{n}: {r}")
実行結果はこうなります。
C: 1.0
D: 1.122462048309373
E: 1.2599210498948732
F: 1.3348398541700344
G: 1.4983070768766815
A: 1.681792830507429
B: 1.8877486253633868
C: 2.0
平均律は、他の音律と異なり、きれいな分数比になりません。
聴き比べる
三種類の音律による音を作ったので、これを聞いてみましょう。まずは周波数比から周波数を作ります。ラの音を440Hzにして、そこからの比で決めます。
freq_p = [440.0 / ratio_p[5] * ratio_p[i] for i in range(8)]
freq_j = [440.0 / ratio_j[5] * ratio_j[i] for i in range(8)]
freq_e = [440.0 / ratio_e[5] * ratio_e[i] for i in range(8)]
for i, r in enumerate(list("CDEFGABC")):
print(f"{r} {freq_p[i]:.2f} {freq_j[i]:.2f} {freq_e[i]:.2f}")
結果はこうなります。左から順番にピタゴラス音律、純正律、平均律です。
C 260.74 264.00 261.63
D 293.33 297.00 293.66
E 330.00 330.00 329.63
F 347.65 352.00 349.23
G 391.11 396.00 392.00
A 440.00 440.00 440.00
B 495.00 495.00 493.88
C 521.48 528.00 523.25
ドレミファソラシド
まずはドレミファソラシドを聞いてみましょうか。周波数を受け取ってドレミファソラシドを演奏する関数を作ります。
def play_all(freq):
rate = 48000
duration = 0.5
x = np.zeros(int(rate * duration * 8))
for i in range(8):
t = np.linspace(0., duration, int(rate * duration))
start = int(rate * duration * i)
end = int(rate * duration * (i + 1))
x[start:end] = np.sin(2.0 * np.pi * freq[i] * t)
return IPython.display.Audio(x, rate=rate, autoplay=True)
聴き比べてみましょう(大きな音がでる可能性があるので注意)。
# ピタゴラス音律
play_all(freq_p)
# 純正律
play_all(freq_j)
# 平均律
play_all(freq_e)
ごめんなさい。僕にはさっぱりわかりません。
和音
もともと音律は和音がきれいに響くように作られています。そこで「ドミソド(CEGC)」の和音を演奏させてみましょう。
def play_CEGC(freq):
rate = 48000
duration = 1.0
rd = int(rate * duration)
x = np.zeros(rd * 4)
t = np.linspace(0., duration * 4, rd * 4)
x[0:rd * 4] += np.sin(2.0 * np.pi * freq[0] * t)
t = np.linspace(0., duration * 3, rd * 3)
x[rd:rd * 4] += np.sin(2.0 * np.pi * freq[2] * t)
t = np.linspace(0., duration * 2, rd * 2)
x[rd * 2:rd * 4] += np.sin(2.0 * np.pi * freq[4] * t)
t = np.linspace(0., duration * 1, rd)
x[rd * 3:rd * 4] += np.sin(2.0 * np.pi * freq[7] * t)
return IPython.display.Audio(x, rate=rate, autoplay=True)
聴き比べてみましょう。
# ピタゴラス音律
play_CEGC(freq_p)
# 純正律
play_CEGC(freq_j)
# 平均律
play_CEGC(freq_e)
うーん、やっぱり僕にはわかりませんね。
うなりを調べる
三種類の音律がたしかに異なる音である、ということを確認するため、同じ音をならして「うなり」が出ることを確認してみましょう。
def play_two(freq1, freq2):
rate = 48000
duration = 4.0
t = np.linspace(0., duration, int(rate * duration))
x = np.sin(2.0 * np.pi * freq1 * t)
x += np.sin(2.0 * np.pi * freq2 * t)
return IPython.display.Audio(x, rate=rate, autoplay=True)
二種類の音律の「ド(C)」を同時に鳴らしてみましょう。
# ピタゴラス音律と純正律
play_two(freq_p[0], freq_j[0])
# 純正律と平均律
play_two(freq_j[0], freq_e[0])
# ピタゴラス音律と平均律
play_two(freq_p[0], freq_e[0])
ピタゴラス音律と純正律のドの周波数の違いは3.26Hz、純正律と平均律のドは2.37Hz、ピタゴラス音律と平均律のドは0.89Hzと、差が小さくなっていくので、それに伴って「うなり」がゆっくりになります。
まとめ
せっかくPythonで好きなように音が作れるようになったので、三種類の音律を作って聴き比べて見ました。残念ながら僕は音律を聞き分ける耳を持っていませんでしたが、音楽に親しんでいるような人は聞き分けられるかもしれません。また、音律を作る手続きがわりとアルゴリズミックで面白いですね。

Discussion