Zenn
🤖

平均二乗変位をフーリエ変換で求める

2021/07/23に公開
Python
math
#
離散フーリエ変換
#
フーリエ変換
tech

概要

ランダムな力を受けて動く粒子がいるとします。その運動方程式は以下のようなランジュバン方程式に従うでしょう。

\frac{dx}{dt} = \hat{R}

ただし、\hat{R}は白色雑音です。この時、時刻tと時刻t+\tauの座標の差の二乗の平均は、その時間\tauに比例します。

\left< \left(x(t) - x(t+\tau) \right)^2 \right> \propto D\tau

この\left< \left(x(t) - x(t+\tau) \right)^2 \right>を、平均二乗変位(Mean Square Displacement, MSD)と呼びます。いま、時間間隔hで座標を観測し、x_k = x(hk)と書きましょう。この離散的な時系列\{x_k\}がN点得られた時(つまりk=0,1,\cdots,N-1)、平均二乗変位D(m)は

D(m) = \frac{1}{N-m} \sum_{k=0}^{N-m-1} \left(x_{k+m} - x_k\right)^2

で定義されます。これはナイーブに計算するとO(N^2)となりますが、フーリエ変換を使うとO(N\ln N)になって、特にNが大きい時に高速になります。それを見てましょう、というのが本稿の趣旨です。

以下のコードはGitHubに公開してあり、Google Colabで直接開くことができます。

Open In Colab

周期境界補正

平均二乗変位を求める前に、周期境界補正について考えます。多くの場合、シミュレーションでは周期境界を用いて計算を行います。すると、注目する粒子が境界を跨ぐ時に、それをちゃんと考慮してやらないと変位がおかしなことになります。まずは周期境界下で座標の時系列xが与えられた時に、周期境界条件の補正をしてやることを考えましょう。

システムサイズをL=10とします。後で必要となるライブラリもインポートしておきます。

import numpy as np
from matplotlib import pyplot as plt
import random
L = 10

粒子がxの正方向に等速直線運動をしており、境界を2回またいだ状態を考えます。こんな感じです。

L = 10
x = [i - (i // L)*L  for i in range(L*3)]
plt.plot(x)
plt.show()

fig

これが、あたかも周期境界がなく、無限の領域を運動していたらどんな軌跡だったかを考えるのが周期境界条件補正です。単純にはこんなことをしてやりたくなります。

def adjust_periodic_wrong(x):
    for i in range(len(x)-1):
        if x[i+1] - x[i] > L/2:
            x[i+1] -= L
        if x[i+1] - x[i] < -L/2:
            x[i+1] += L

要するに、一つ前の座標とL/2以上離れていたらLだけ補正するものです。しかし、これはうまくいきません。

x = [i - (i // L)*L  for i in range(L*3)]
adjust_periodic_wrong(x)
plt.plot(x)
plt.show()

fig

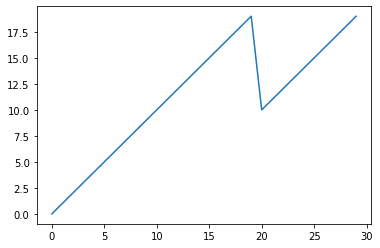
このように、二回境界をまたぐケースでおかしくなります。

正しくはこうしてやる必要があります。

def adjust_periodic(x):
    for i in range(len(x)-1):
        if x[i+1] - x[i] > L/2:
            x[i+1] -= (x[i+1] - x[i]+L/2)//L*L
        if x[i+1] - x[i] < -L/2:
            x[i+1] += (x[i] - x[i+1]+L/2)//L*L

何回境界をまたいだかを計算し、その分だけ補正してやります。結果はこうなります。

x = [i - (i // L)*L  for i in range(L*3)]
adjust_periodic(x)
plt.plot(x)
plt.show()

fig

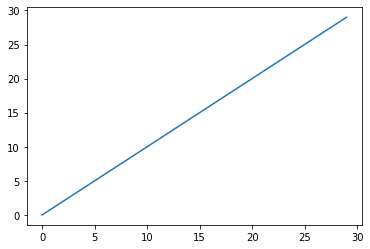
ちゃんとまっすぐになりましたね。

念のため逆方向も確認しておきましょう(基本)。

x = [-i - (-i // L)*L  for i in range(L*3)]
plt.plot(x)
plt.show()
adjust_periodic(x)
plt.plot(x)
plt.show()

fig
fig

大丈夫そうです。

ランダムウォーク

時系列の作成

それでは、ランダムウォークのデータを作りましょう。単に毎ステップ、-1か+1にランダムで進むだけのコードです。ただし、周期境界条件により0<x<Lとなるようにしています。

def diffusion(step):
    x = np.zeros(step)
    pos = 0.0
    for i in range(step):
        pos += random.choice([-1,1])
        if pos < 0:
            pos += L
        if pos > L:
            pos -= L
        x[i] = pos
    return x

実行結果はこんな感じです。

random.seed(12345)
x = diffusion(2**12)
plt.plot(x)
plt.show()

fig

周期境界によりよくわからなくなっています。補正してやりましょう。

adjust_periodic(x)
plt.plot(x)
plt.show()

fig

それっぽくなりました。以後、この軌跡について平均二乗変位を計算します。

シンプルな計算

まずは、定義式

D(m) = \frac{1}{N-m} \sum_{k=0}^{N-m-1} \left(x_{k+m} - x_k\right)^2

をそのまま計算してやりましょう。こうなるでしょうか。

def calc_msd_simple(x):
    n = len(x)
    msd = []
    for s in range(1,n//4):
        x2 = 0.0
        for i in range(n-s):
            x2 += (x[i+s]-x[i])**2
        x2 /= (n-s)
        msd.append(x2)
    return msd

そのままなので、特に難しくはないと思います。ただし、mがNに近いとサンプル数が少なくなってしまうため、0<m<N/4としました。

平均二乗変位をプロットしてやりましょう。ついでに時間を測ってみます。

%%time
msd_simple = calc_msd_simple(x)
plt.plot(msd_simple)
plt.show()

fig

CPU times: user 3.32 s, sys: 16.7 ms, total: 3.34 s
Wall time: 3.34 s

3.34秒かかりました。

NumPyっぽく計算

シンプルな計算では遅すぎるので、ちょっとPythonっぽく計算してみましょう。欲しいのは、インデックスがsだけずれた座標の差です。PythonはN個の要素を持つ配列aにたいしてa[s:]とするとa[s].a[s+1],...a[N-1]の部分配列を、a[:-s]とすると、a[0],a[1],...,a[N-s-1]の部分配列を返します。

a = np.arange(10)
a[2:]  # => array([2, 3, 4, 5, 6, 7, 8, 9])
a[:-2] # => array([0, 1, 2, 3, 4, 5, 6, 7])

なので、a[s:] - a[:-s]により、sだけ離れたインデックスの差の配列を得ることができます。差を計算するのも二乗を計算するのもNumPy配列の演算になるので、高速化が期待できます。コードに落とすとこんな感じになるでしょう。

def calc_msd_np(x):
    n = len(x)
    msd = []
    for s in range(1,n//4):
        dx = x[s:] - x[:-s]
        msd.append(np.average(dx**2))
    return msd

実行して時間を測ってみます。

%%time
msd_np = calc_msd_np(x)
plt.plot(msd_np)
plt.show()

fig

CPU times: user 151 ms, sys: 0 ns, total: 151 ms
Wall time: 156 ms

実行時間は156 msと、かなり高速化されました。

念のために二つを重ねてみましょう。

fig, ax = plt.subplots()
ax.plot(msd_simple,label="Simple")
ax.plot(msd_np,label="NumPy")
ax.legend()

fig

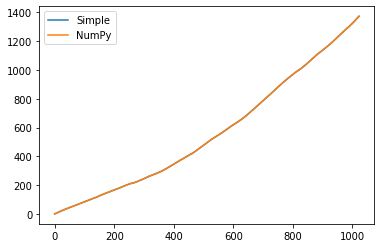
完全に一致していますね。

フーリエ変換

さて、フーリエ変換のお時間です。何かを高速に計算しようとすると、やたらと顔を出す高速フーリエ変換(Fast Fourier Transform, FFT)ですが、ここにも顔を出してきます。まずは平均二乗変位の定義をバラします。

\begin{aligned} D(m) &= \frac{1}{N-m} \sum_{k=0}^{N-m-1} \left(x_{k+m} - x_k\right)^2 \\ &= \underbrace{\frac{1}{N-m} \sum_{k=0}^{N-m-1} \left(x_{k+m}^2 + x_k^2\right)}_{s_1} - 2 \times \underbrace{\frac{1}{N-m} \sum_{k=0}^{N-m-1} x_{k+m} x_k}_{s_2}\\ &= s_1 -2 s_2 \end{aligned}

まず、s_1の項は、要するに時系列の2乗の平均の2倍です。なので、

s1 = np.average(x**2)*2

と計算できます。s_2は自己相関関数です。ウィーナー・ヒンチンの定理により、自己相関関数はパワースペクトルとフーリエ変換の関係にあるのでした。なので、まずはxをフーリエ変換し、その絶対値の二乗を計算してから逆フーリエ変換してやると自己相関関数が求まります。以上を実装してやるとこうなります。

def calc_msd_fft(x):
    n=len(x)
    fk = np.fft.fft(x, n=2*n)
    power = fk * fk.conjugate()
    res = np.fft.ifft(power)[:n].real
    s2 = res/(n*np.ones(n)-np.arange(0,n))
    s1 = np.average(x**2)
    msd = 2*s1 - 2*s2
    return msd[:n//4]

実行しましょう。

%%time
msd_fft = calc_msd_fft(x)
plt.plot(msd_fft)

fig

CPU times: user 17.7 ms, sys: 989 µs, total: 18.7 ms
Wall time: 20.5 ms

20.5 msとなりました。早いですね。

念のため、ナイーブな方法で得られたものと重ねてみましょう。

fig, ax = plt.subplots()
msd_np = calc_msd_np(x)
msd_fft = calc_msd_fft(x)
ax.plot(msd_np,label="NumPy")
ax.plot(msd_fft,label="FFT")
ax.legend()
plt.show()

fig

ちょっとずれてしまいました。これは、s_1の計算を真面目にやらなかったためです。本当は

s_1 = \frac{1}{N-m} \sum_{k=0}^{N-m-1} \left(x_{k+m}^2 + x_k^2\right)

でしたが、これを、

s_1 \sim \frac{2}{N} \sum_{k=0}^{N-1} x_k^2

と近似しました。これはわりと良い近似なので別にこのままでも良い気がしますが、気になるならちゃんと計算しましょう。先ほど触れた「ちょっとずらした和」を使えば簡単です。ただし、差が0のところだけは別扱いにする必要があります。

s1 = np.zeros(n)
s1[0] = np.average(x2)*2.0
for m in range(1,n):
    s1[m] = np.average(x2[m:] + x2[:-m])

これを使うとこうなるでしょう。

def calc_msd_fft2(x):
    n=len(x)
    fk = np.fft.fft(x, n=2*n)
    power = fk * fk.conjugate()
    res = np.fft.ifft(power)[:n].real
    s2 = res/(n*np.ones(n)-np.arange(0,n))
    x2 = x**2
    s1 = np.zeros(n)
    s1[0] = np.average(x2)*2.0
    for m in range(1,n):
        s1[m] = np.average(x2[m:] + x2[:-m])
    msd = s1 - 2*s2
    return msd[:n//4]

重ねてみましょう。

fig, ax = plt.subplots()
msd_np = calc_msd_np(x)
msd_fft2 = calc_msd_fft2(x)
ax.plot(msd_fft2,label="FFT2")
ax.plot(msd_np,label="NumPy")
ax.legend()
plt.show()

fig

ぴったり一致しました。

まとめ

平均二乗変位をフーリエ変換を使って計算するサンプルを紹介しました。実際に分子動力学計算などで得られた結果を解析するには、周期境界条件補正が必要となります。補正してしまえば、あとは普通にフーリエ変換するだけです。なんとなく「自己相関関数はフーリエ変換で求められるんだったな」「平均二乗変位もフーリエ変換で求められるんだったな」と覚えていても、実際に書こうとすると「あれ？」となるものです。っていうかなりました。

この記事が誰かの役に立てば幸いです。

参考

GitHubで編集を提案

Discussion