はじめに
ルジャンドル変換は、自由変数を取り直す変換のことで、双対変換の一種です。双対変換というのは、ざっくり言えば「変換したあと、もう一度変換したらもとにもどる奴」のことです。
例えば正六面体の各面の重心を結ぶと、正八面体になります。この時「正六面体→正八面体」の変換は「面」と「点」の入れ替えに対応しています。同様に、正八面体の各面の重心を結ぶと、正六面体が出てきます。このように、双対変換は「入れ替え」を二度したらもとに戻ります。
また、「AならばB」という命題に対して、「Bでないなら、Aではない」のような命題は対偶と呼ばれますが、両者の真偽は一致します。これも双対です。フーリエ変換やラプラス変換のように、逆変換してもとに戻るやつはだいたい双対変換といって良いでしょう。
このルジャンドル変換の説明として、接線を用いる表式と、面積を用いる表式があります。どちらも同じことを表現していますが、わりと両者の繋がりは不明瞭です。本稿では、両方の気持ちを説明してみようと思います。以下、数学的な厳密さはさておくので、supだのinfだのは出てきません。
接線表式
(x,y)平面における曲線を考えます。xを自由変数として、曲線をy=y(x)と表現しましょう。
二次元平面における曲線とは、点(x,y)の集合です。
さて、曲線上の点(x,y)における接線を考えます。この接線を表す式を
と書きましょう。これは傾きX、切片Yの直線を表しています。
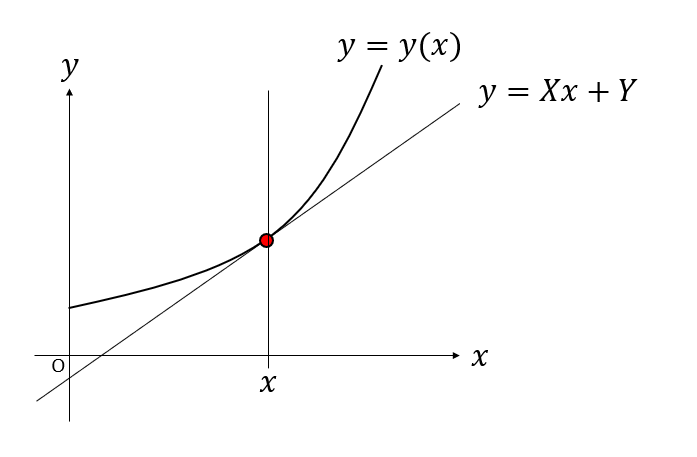
接線の定義からすぐに
\begin{aligned}
X &= \frac{dy}{dx} \\
Y &= y - x \frac{dy}{dx}
\end{aligned}
であることがわかります。これが(x,y)から(X,Y)へのルジャンドル変換で、(x,y)で表現される点の集合を、(X,Y)で表現される直線の集合に入れ替えた、つまり「点」と「線」を入れ替えたことに対応します。
次に、(X,Y)の集合を曲線Y=Y(X)だと思ってルジャンドル変換してみましょう。
\begin{aligned}
\frac{dY}{dX} &= \frac{dY}{dx}\frac{dx}{dX} = -x\\
Y-X \frac{dY}{dX} &= y - x \frac{dy}{dx} + x \frac{dy}{dx} = y
\end{aligned}
ここから、(X,Y)から(x,y)に戻すルジャンドル逆変換は、
\begin{aligned}
x &= - \frac{dY}{dX}\\
y &= Y-X \frac{dY}{dX}
\end{aligned}
となります。
順変換と逆変換を並べてみましょう。
\left(
\begin{array}{ccc}
X &=& \displaystyle\frac{dy}{dx}\\
Y &=& y-x \displaystyle \frac{dy}{dx}
\end{array}
\right.
\qquad
\left(
\begin{array}{ccc}
x &=& - \displaystyle\frac{dY}{dX}\\
y &=& Y-X \displaystyle \frac{dY}{dX}
\end{array}
\right.
形はほとんど同じですが、逆変換のxの表式に負符号がついています。これを嫌って、接線の式をy = Xx - Yと、切片に負符号をつける流儀もあります。すると、負符号がキャンセルして、
\left(
\begin{array}{ccc}
X &=& \displaystyle\frac{dy}{dx}\\
Y &=& x \displaystyle \frac{dy}{dx} -y
\end{array}
\right.
\qquad
\left(
\begin{array}{ccc}
x &=& \displaystyle\frac{dY}{dX}\\
y &=& X \displaystyle \frac{dY}{dX} -Y
\end{array}
\right.
と、順変換と逆変換が同じ表式になります。
ここで、最終的にもとに戻るならどのような定義を用いても構わないことに注意しましょう。同様な事例に「フーリエ変換で2\piをどちらに押し付けるか問題」があります。工学では順変換には2\piはつけず、逆変換にすべて押し付けますが、数学では対称性を重視してどちらにも\sqrt{2\pi}をつけたりします。最終的につじつまが合えばどちらを採用してもかまいません。
面積表式
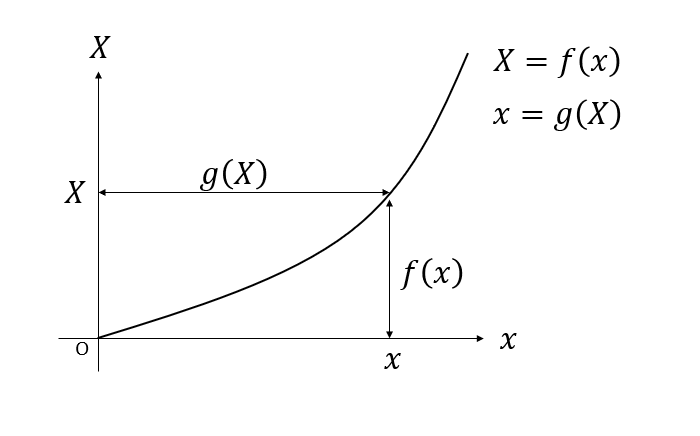
(x,X)空間を考えます。この空間における曲線を考えます。xを自由変数に取るならX=f(x)、Xを自由変数にとるならx=g(X)と表現できます。fとgはお互いに逆関数です。
ここで、f(x)を積分したものをyを、g(X)を積分したものをYと定義します。
\begin{aligned}
y &= \int_0^x f(x) dx \\
Y &= \int_0^X g(X) dX
\end{aligned}
もともとX=f(x)、y=g(X)でしたから、定義から
X = \frac{dy}{dx} , x = \frac{dY}{dX}
となります。
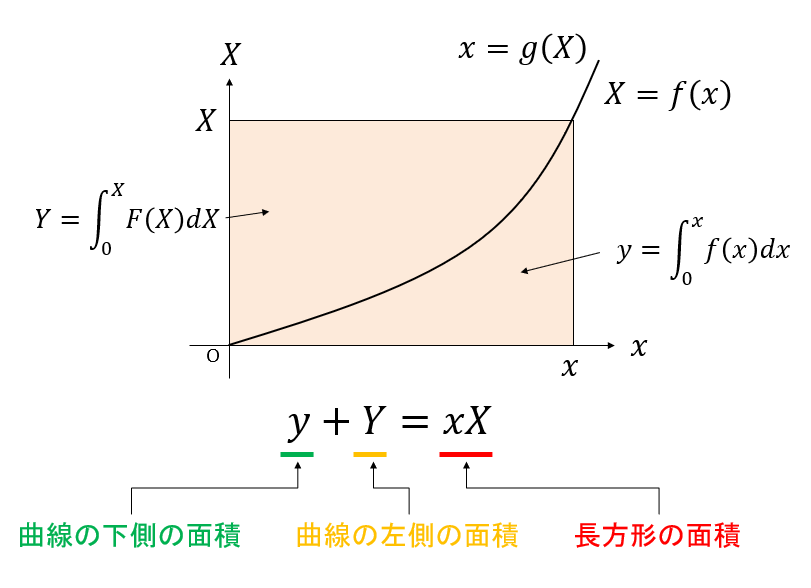
さて、上の図において長方形が曲線で分割されていると考えると、長方形の面積がxX、曲線の下部分の面積がy、曲線の左部分の面積がYなので、
となります。ここからただちに(x,y)と(X,Y)の間の変換式が求まります。
\left(
\begin{array}{ccc}
X &=& \displaystyle\frac{dy}{dx}\\
Y &=& x \displaystyle \frac{dy}{dx} - y
\end{array}
\right.
\qquad
\left(
\begin{array}{ccc}
x &=& \displaystyle\frac{dY}{dX}\\
y &=& X \displaystyle \frac{dY}{dX} - Y
\end{array}
\right.
こちらは、自然に順変換と逆変換が同じ形となります。
ルジャンドル変換の例
大学の物理においてルジャンドル変換は、力学のラグランジアンからハミルトニアンを導くところや、熱力学の自由変数の取り替えなどに現れます。
物理で現れるルジャンドル変換の対象は一般の多変数ですが、注目する変数以外を固定し、一変数関数だと思って変換すれば、常微分が偏微分方になるだけであとは同じです。
さて、\dot{q},qの関数であるラグランジアンL(\dot{q},q)を考えます。qを固定し、この第一引数に関してルジャンドル変換しましょう。これを(\dot{q}, L)から、(p, H)への変換だと思えば、
\begin{aligned}
p &= \frac{\partial L}{\partial \dot{q}} \\
H &= pq- L
\end{aligned}
となります。これは、順変換と逆変換が同じ形になるタイプのルジャンドル変換です。
次に、内部エネルギーUが、エントロピーSと体積Vの関数としてU=U(S,V)与えられているとしましょう。体積Vを固定し、Sに関してルジャンドル変換し、それを(S,U)から(T F)への変換だと思えば、
\begin{aligned}
T &= \frac{\partial U}{\partial S} \\
F &= U - TS
\end{aligned}
となります。これは、逆変換に負符号が出るタイプのルジャンドル変換です。U=TS + Fと書けば、(S,U)空間において、ある点での接線を表す式になっており、Tがその傾き、Fが切片になっていることがわかります。
熱力学では、変換が対称であることより、熱力学関数の凸の向きが変換後も同じであった方が便利なので、こちらの定義を採用しています。
まとめ
ルジャンドル変換の二つの表式を比べてみました。ルジャンドル変換によって(x,y)から(X,Y)に移る時、
として「接線」を考えるタイプと、
として面積を考えるタイプがあります。
面積を考えるタイプは、(x,y)と(X,Y)が完全に対等であることがわかりやすく、自然に順変換と逆変換が等しくなります。また、途中に微分不連続点があっても定義可能です。
一方、説明に使う図が(x,X)空間であり、我々の興味ある物理量であるラグランジアンLや内部エネルギーUが図に直接現れない(積分として現れる)のがちょっとわかりづらいかな、という気がします。
接線を考えるタイプは、ルジャンドル変換が「点」と「直線」の双対変換である、ということがわかりやすい気がします。また、興味ある物理量が直接図に出てきます。
一方で、ナイーブな定義では、逆変換に負符号が現れてしまい、(x,y)と(X,Y)が対等であることが見えづらい気もします。
個人的には「双対変換」であることがわかりやすい接線タイプの説明が好きですが、表式がきれいな面積タイプの説明を好む人がいるのも理解できます。
本稿が、両者をつなぐ理解の助けになれば幸いです。


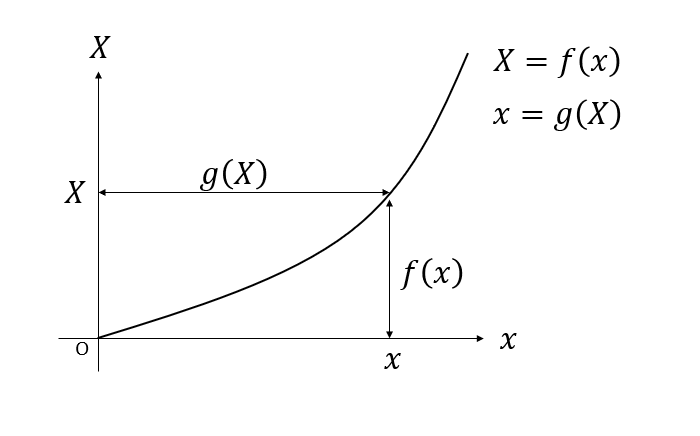

Discussion
なるほど、面白いですね!補足というか、少し整理しました。
曲線をxy平面上で表現する場合、素朴には
\{(x,y) | (\rm{some \ condition})\}
\{(x,f(x)) | x \in \mathrm{R} \}
\{l | (\rm{line,\ some \ condition})\}
とくに関数で定められる場合は
という点集合として捉えることができます。一方で、これは適当な直線の集合
の包絡線と考えることもできるわけですね。
そこで、これらの2つの集合の間の対応を考えるとき、l xy
l: y = Xx - Y (x_0,y_0) X_0, Y_0
y_0 = X_0 x_0 - Y_0 x_0, y_0 x, y
y = Xx - Y
と表すことにすると(切片を負としました)、曲線上の点
を満たすように取ることができる。(というのは、
そこで、記号の濫用で
とかく。ということですね。
ところで、(原点を通る単調な)曲線には上記のものとまた別の表現方法もあって、以下本文と少し文字が違いますが、
\{(x,s) | s = \int_0^x ydx \} (x,y) x s \{(y, S) | S = \int_0^y xdy \}
xy = s + S
つまり、単純な点の座標
このとき、yについても同様に
が成り立つ。
ここでy=f(x)=X X X
なので、これによって(x,s) (X,S)=(y,S) (x,s) (X,S)
上述の点と接線の対応(x,y) \mapsto (X,Y) (x,s) \mapsto (X,S)
ということなんですね。なるほど、勉強になりました。
ところで、このコメントをした2022/3/18 20:30頃現在では、面積の方の変換式のy Y
(順変換と逆変換が同じという結論は変わりませんが、
かなと思いました)
整理をありがとうございます。おっしゃる通りの理解と思います。
また、面積の方の変換式は符号が間違っていますね。コピペミスをしていました。修正しておきました。こちらもありがとうございます。