ルジャンドル変換と双対の話
はじめに
理工系の学生なら、熱力学や解析力学の講義でルジャンドル変換を学んだと思います。ルジャンドル変換は独立変数を取りかえるための変換ですが、これが何をやっているか、どういう意味を持っているかがよくわからない人も多いと思います。幾何学的に見ると、ルジャンドル変換は「点」と「線」を入れ替える双対変換になっています。この双対という考え方はいろんなところに現れます。以下、点と線、点と面の双対変換についてつらつら書いてみたいと思います。
ルジャンドル変換
関数
さて、この曲線の、ある点
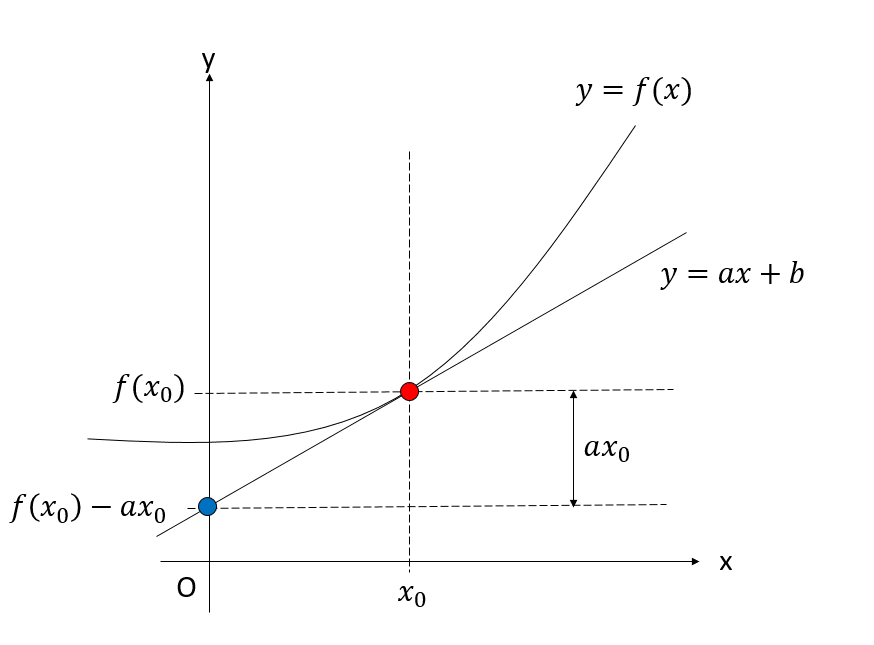
ここでは、
という変換が導かれます。
多変数関数の場合も、他の変数を固定し、注目する変数での微分、つまり偏微分になるだけで全く同じです。例えば
が得られます。ここで
となり、見慣れた変換公式が現れました。変換の幾何学的な意味は、単に
パスカルの定理とブリアンションの定理
ルジャンドル変換は、曲線上の点を、その点での接線と入れ替える「点と直線」の双対変換になっていました。この「点と直線」の双対変換でもっとも有名なのはパスカルの定理とブリアンションの定理の関係でしょう。
まず、パスカルの定理とは、「円に内接する六角形の、対面にある辺を延長して得られる三つの交点が一直線上に並ぶ」というものです。
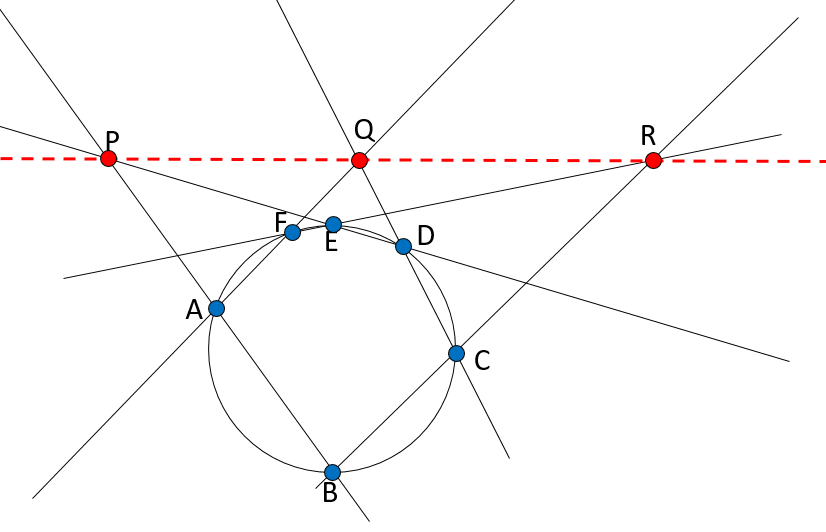
上記の図では、例えば六角形ABCDEFの、辺ABとEDを延長して得られる交点P、AFとCDをから得られるQ、EFとBCから得られる点Rが一直線上に並んでいます。
さて、この「点と直線」を双対変換で入れ替えてみましょう。
まずは、ABCDEFの各点で、円に対する接線を引きます。すると、円に外接する六角形が得られます。

得られた六角形の、対面する点を結ぶ線を引くと、一点で交わります。これが「ブリアンションの定理」です。

ここで、「点」が「直線」に、「直線」が「点」に入れ替わっています。パスカルの定理とブリアンションの定理を並べてみましょう。

パスカルの定理においてm辺ABを結ぶ直線をα、辺EDを結ぶ直線をδとしましょう。ブリアンションの定理では、α、δはそれぞれ「点」になります。パスカルの定理において「直線」αとδの「交点」Pは、ブリアンションの定理では、「点」αとδを結ぶ「直線」Pになっています。「点P,Q,Rが一直線上θに並ぶ」という命題は、「直線P,Q,Rが一点θで交わる」という命題に変換されます。
このように、お互いに双対の関係にある命題を双対命題と呼びます。幾何学で有名なのはパスカルの定理とブリアンションの定理ですが、他にも論理式で論理和∨と論理積∧、全称記号∀と存在記号∃をそれぞれ入れ替えることで双対命題が得られます。双対命題は真偽が一致します。
正多面体
双対変換で面白いのが正多面体の双対です。先ほどまでは「点」と「線」を入れ替えましたが、今度は「点」と「面」を入れ替えてみましょう。
まずその前に正多面体を構築してみましょう。正多面体は、全て正多角形で構成された立体です。例えばサイコロ、つまり正六面体は、全て正方形(正四角形)でできています。正六面体の頂点を見ると、正方形が3つ集まっています。正四面体は正三角形が、頂点に3つ集まっています。このように正多面体は「正
まず、
| m | n | 立体 |
|---|---|---|
| 3 | 3 | 正四面体 |
| 3 | 4 | 正八面体 |
| 3 | 5 | 正二十面体 |
| 4 | 3 | 正六面体 |
| 5 | 3 | 正十二面体 |
ここで、「面」の中心(重心)を考え、その中心を線で結んでみます。例えば、正六面体の各面の中心を結ぶと、正八面体が出てきます。

先の「各頂点に
同様にして、正十二面体
正多面体の双対はよく知られていますが、こうして
まとめ
ルジャンドル変換は曲線上の接点における接線を考え、「点」の代わりに「線」で曲線を表現する「点」と「線」の双対変換になっています。こういう見方をすると、なぜ
なお、ルジャンドル変換は逆変換で負符号が出ないような定義をとることが多いですが、熱力学などでは凸性が入れ替わることを嫌って、逆変換で負符号が出る定義を採用したりします。これもフーリエ変換で片方の変換に
他にも「点」と「面」をはじめとしていろんな双対があります。実験をする研究室に配属された学生さんは、X線回折などで逆格子が出てくることを学んだでしょう。あれも双対です。
このようにルジャンドル変換や、正多面体、X線回折画像など、一見全くことなるように見えるものに「双対」という共通する見方が存在するのが数学の面白さです。
本稿が「ルジャンドル変換わからん」という学生さんの助けになれば幸いです。
Discussion