概要
誤差伝播の公式というものがある。なにか誤差がある量を加減乗除したときに、誤差がどのようになるか、ということを教えてくれる公式だ。例えば、いまXという量が、\Delta Xという誤差を、Yという量が\Delta Yという誤差を持っているとき、その積であるXYの誤差はどうなりますか?ということを問うのが誤差伝播である。
実験などでは、測定値の和や差より積を計算することが多いため、積の誤差伝播公式をよく使う。X \pm \Delta XとY \pm \Delta Yの積は、
\begin{aligned}
(X + \Delta X)(Y + \Delta Y) &= XY + X\Delta Y + Y \Delta X + \Delta X \Delta Y \\
&\sim XY + X\Delta Y + Y \Delta X
\end{aligned}
と\Delta X \Delta Yを高次の項として無視して、最終的に
(X \pm \Delta X)(Y \pm \Delta Y) \sim XY \pm (X\Delta Y + Y \Delta X)
と書き、X\Delta Y + Y \Delta Xを誤差をみなす、というのが一般的だ。これは、以下のように面積図で説明されることが多い。
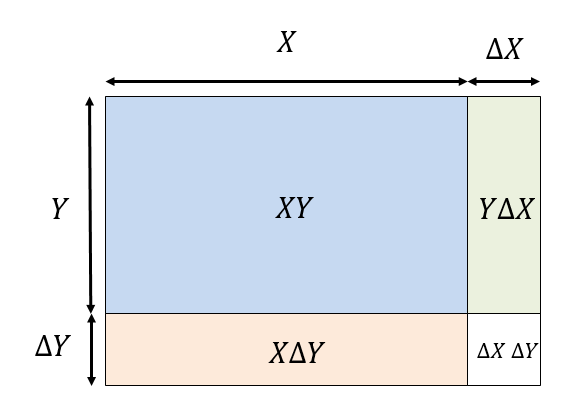
自分の誤差(\Delta X)が、相方(Y)によって引き延ばされる(Y \Delta X)ようなイメージだ。
もしくは、テイラー展開による説明を聞いたかもしれない。ある変数Xの関数f(X)について、Xが\Delta Xだけずれた影響は一次のテイラー展開で
f(X+\Delta X) \sim f(X) + f'(X) \Delta X
と書けるため、誤差\Delta Xはf'(X)により引き延ばされる。今は、二変数なのでf(X,Y) = XYとして、二変数関数の一次のテイラー展開をすれば、同じ結果が得られる。
以上の説明は非常にわかりやすいのだが、テキストなどで、「以下の公式の方が正しい(より正確だ)」と説明されて混乱する人がいる。
(X \pm \Delta X)(Y \pm \Delta Y) \sim XY \pm \sqrt{X^2\Delta Y^2 + Y^2 \Delta X^2}
本稿では、上記の誤差伝播の公式をちゃんと導出して、なぜ後者の方が「良い」公式なのかを説明する。
誤差とはなにか
誤差という言葉が意味するものは難しい。たとえば実験で定規を使ってなにかの長さを測定したとき、メモリは1mmまでしかないが、目分量で0.1mmまで値を読みなさい、と指導されることがある。このとき、当然ながら0.01mm以下の長さについてはまったく情報がないし、0.1mmの値だって怪しいであろう。すると、全く同じものを別の人が測定した場合(もしくは同じ人が別の日に測定した場合)、値がばらつくことになる。
そこで、何度も測定して、その平均値を測定値としたくなる。例えば10回測定した平均値を考えるとき、さらに10回測定するとまた異なる平均値になるであろう。つまり、測定値を確率変数とみなすことができる。
以後、確率変数を\hat{X}のようにハットをつけて表現しよう。確率変数\hat{X}に対する期待値を\left< \hat{X} \right>とする。期待値は、以下のような線形性を満たす。
\left< a \hat{X} + b \hat{Y} \right> =
a \left<\hat{X}\right> +
b \left<\hat{Y}\right>
また、確率変数\hat{X}と確率変数\hat{Y}が独立である時、積の期待値が期待値の積で書ける。
\left<\hat{X}\hat{Y}\right> = \left<\hat{X}\right>\left<\hat{Y}\right>
ある確率変数\hat{X}について期待値\mu_Xと分散\sigma_X^2を以下のように定義する。
\begin{aligned}
\mu_X &\equiv \left< \hat{X} \right> \\
\sigma_X^2 &\equiv \left< (\hat{X} - \mu_X)^2 \right>
\end{aligned}
このとき、標準偏差\sigma_Xを「誤差」とみなし、\hat{X}の測定値Xを
と表記することを約束する。つまりここでは「誤差」を「測定値を確率変数とみなした場合の標準偏差」であるとする。
以上で準備が整った。我々は、平均値がそれぞれ\mu_X, \mu_Y、分散が\sigma_X^2, \sigma_Y^2であるような確率変数\hat{X}と\hat{Y}について、その期待値\mu_{XY}と分散\sigma_{XY}^2を求め、最終的に
XY = \mu_{XY} \pm \sigma_{XY}
と書きたい。簡単のため、平均値は正(\mu_X > 0,\mu_Y > 0)であるとする。また、\hat{X}と\hat{Y}は独立であるとする。すると\mu_{XY} = \mu_X \mu_Yである。
したがって、求めたいのは\sigma_{XY}である。真面目に定義から計算しよう。
\begin{aligned}
\sigma_{XY}^2 & \equiv \left< (\hat{X}\hat{Y} - \mu_X \mu_Y)^2\right>\\
&= \left<\hat{X}^2\hat{Y}^2\right> - 2\mu_X \mu_Y \left<\hat{X} \hat{Y}\right> + \mu_X^2 \mu_Y^2\\
&= \left<\hat{X}^2\right> \left<\hat{Y}^2\right> -\mu_X^2 \mu_Y^2\\
&= \mu_X^2 \sigma_Y^2 + \mu_Y^2 \sigma_X^2 + \sigma_X^2 \sigma_Y^2\\
&= \mu_X^2 \mu_Y^2 \left( \frac{\sigma_X^2}{\mu_X^2}+ \frac{\sigma_Y^2}{\mu_Y^2}+ \frac{\sigma_X^2}{\mu_X^2}\frac{\sigma_Y^2}{\mu_Y^2} \right) \\
&= \mu_X^2 \mu_Y^2 \left(\varepsilon_X^2+\varepsilon_Y^2+ \varepsilon_X^2\varepsilon_Y^2\right)
\end{aligned}
ただし最後で、\sigma_X^2/\mu_X^2 = \varepsilon_X^2、\sigma_Y^2/\mu_Y^2 = \varepsilon_Y^2と表記した。
さて、もとの分布がどんなであれ、何度も測定を繰り返して平均値を計算すれば、その平均値の分布はガウス分布に近づき、サンプル数を増やすほどその分散が小さくなる(中心極限定理)。したがって、十分な回数の観測を行えば、平均値の絶対値に対して分散が十分に小さくなるであろう。いま、\varepsilon_Xと\varepsilon_Yがどちらも\varepsilonのオーダーであるとし、\varepsilon \ll 1であるとしよう。すると\varepsilon_X^2 \sim \varepsilon_Y^2 \sim \varepsilon^2に対して\varepsilon_X^2\varepsilon_Y^2は \sim \varepsilon^4と高次の項になるため無視して良い。
以上から、
\begin{aligned}
\sigma_{XY}^2 &\sim \mu_X^2 \mu_Y^2 \left(\varepsilon_X^2+\varepsilon_Y^2\right)\\
&= \mu_X^2 \sigma_Y^2+\mu_Y^2 \sigma_X^2
\end{aligned}
である。したがって、
XY = \mu_X \mu_Y \pm \sqrt{\mu_X^2 \sigma_Y^2+\mu_Y^2 \sigma_X^2}
これが「正確な方」の公式である。
さて、実用的には平方根が面倒なので外したい。
\sigma_{XY}^2 = \mu_X^2 \mu_Y^2 \left(\varepsilon_X^2+\varepsilon_Y^2\right)
であったのを、右辺の括弧の中に2 \varepsilon_X \varepsilon_Yを足してやろう。すると平方完成することができる。
\begin{aligned}
\sigma_{XY}^2 &= \mu_X^2 \mu_Y^2 \left(\varepsilon_X^2+2 \varepsilon_X \varepsilon_Y+ \varepsilon_Y^2\right)\\
&= (\varepsilon_X + \varepsilon_Y)^2
\end{aligned}
すると、最初に現れた方の公式
XY = \mu_X \mu_Y \pm (\mu_X \sigma_Y + \mu_Y \sigma_X)
が得られた。ここで注意したいのは、先ほど足した\varepsilon_X \varepsilon_Yは\varepsilon^2のオーダーであり、\varepsilon_X^2,\varepsilon_Y^2に対して無視できない量である。
簡単のため、\mu_X=\mu_Y=\mu, \sigma_X = \sigma_X = \sigmaとすると、正確な方の公式の誤差は\sqrt{2} \mu \sigma、後者の公式は2 \mu \sigmaとなり、\sqrt{2}倍だけ誤差を過大評価している。
これは、後者の公式では、XとYの平均値からのずれ方(ずれる方向)が同じであると仮定してしまっているからだ(最初の面積図を参照)。Xが平均から大きくなる方向にずれた時、Yは平均から小さくなることもあるため、「誤差」は打ち消しあうこともある。それが\sqrt{2}倍の違いとして現れている。
まとめ
測定値の積の誤差の伝播について、以下の二つの公式が用いられる場合がある。
(X \pm \Delta X)(Y \pm \Delta Y) \sim XY \pm X\Delta Y + Y \Delta X
(X \pm \Delta X)(Y \pm \Delta Y) \sim XY \pm \sqrt{X^2\Delta Y^2 + Y^2 \Delta X^2}
これは、測定値を確率変数だと思って、「誤差」を確率変数の標準偏差だと思うならば、後者の方が正確であり、前者は「誤差」を過大評価する。その理由は、前者が複数の変数が「同じように揺らぐ」と仮定してしまっているからだ。
しかし、実際の測定誤差は数%以下のオーダーであることが多く、それが1.4倍に評価されても大きな問題にならないことが多い。ちゃんとした論文であれば気を付けた方が良いが、学生実験くらいならあまり気にしなくて良いような気がする(とか書いたら怒られる?)。
関連記事

Discussion
(長文コメントすみません。)
Xbyakなどいつも楽しい記事ありがとうございます。
統計誤差(statistical uncertainty)と系統誤差(systematic uncertainty)があるという説明を飛ばして、どちらの公式が『正確』というのは若干混乱を招くように感じました。
測定値を確率変数だと思って、の部分にその前提が含まれているのだと思いますが、対象読者と思われる初学者(?)は読み流してしまうかもと。
系統誤差の場合、揺らいでいるわけではないので、テイラー展開型の取扱いが適切だと思っています。
また、\sqrt{2} \Delta X > 0 \Delta Y<0
(テイラー展開でも、
『独立した2つの分布の同時分布を考えたときに、稀な値と稀な値が同時に起きる確率は更に稀になる』が\sqrt{2}
コメントをありがとうございます。統計誤差と系統誤差の説明についてはおっしゃる通りですね。ただ、理工学系の学生さんが最初に実験とかで誤差を説明を受ける時は、「誤差」はほぼ「統計誤差」を指すので、系統誤差は後で良いのかな・・・と。ちゃんと説明した方が良いのはその通りです。
例えば\hat{X} \hat{Y} \mu \sigma^2 \hat{X}\hat{Y} 2\mu^2\sigma^2 4\mu^2\sigma^2 \sqrt{2}
で、共分散の効果を、「二つの確率変数の平均値からのずれ方が同じ」と表現するか、「稀な値と稀な値が同時に起きる確率は更に稀になる」と表現するかは、表現の問題で、同じことを言っているのかな、と思います。
返答ありがとうございます。
記載の意図理解しました。
そうですね、共分散について触れるのが1番誤解を生まない解釈ですね。
また、素敵な記事お待ちしています。