TL;DR
Q: なぜ最速降下曲線問題の解に角度が出てくるんですか?
A: この問題がスネルの法則の連続極限とみなすことができるから。
はじめに
重力により坂道を摩擦なく滑る物体を考えます。始点と終点を固定した場合、始点からもっとも早く終点にたどり着く曲線はどのようなものでしょうか?

エネルギー保存則により、終点での速度は、始点と終点での高さの差だけに依存します。したがって、どのような経路を辿ろうとも、終点に達した時の速度は同じです。さて、始点と終点を最短距離で結ぶと直線になります(図の黒線)。しかし、この直線よりも少し「深い」曲線(図の赤線)を作ると、距離は損をしますが、直線の場合よりも先に速い速度に達するため、トータルで得をする場合があります。しかし、もっと深くして最初になるべく速度を稼ぐ経路(図の青線)では、速度が早くなる効果よりも走破すべき距離が長くなり過ぎる効果の方が大きく、到達時間が遅くなります。結局、その間にちょうど良い曲線がありそうです。その曲線を求めなさい、というのが最速効果曲線問題です。
この問題は、変分原理の例題としてよく出てきます。図のようにy軸を下向きとする座標をとって、原点を始点とする時、求めたい曲線を
という形に書くと、f(x)が満たすべき微分方程式が出てきます。その微分方程式を解くと、
\begin{aligned}
x &= a (s - \sin \phi), \\
y &= a (1 - \cos \phi).
\end{aligned}
という媒介変数表示を得ます。これは、半径aの円がx軸に接しながらすべらずに角度\phiだけ回転する時、円弧上の点が描く軌跡、すなわちサイクロイド曲線を表しています。

多くの本では、天下り的にこの媒介変数表示を出して、「これがさっきの微分方程式を満たすでしょ」という形で解であることを確認しますが、それでは、なぜ回転角のようなものが出てくるのかが不明瞭なままです。
本稿では、この媒介変数の角度がスネルの法則の角度に由来することを説明します。
定式化

まずはf(x)が満たすべき式を導出しましょう。xの区間をN等分し、一つの区間の長さを\Delta xとします。i\Delta x < x \le (i+1)\Delta xの区間を「区間i」と名付けましょう。それぞれの区間では曲線が直線で近似できるとする、折れ線近似を採用します。区間iにおいて、曲線のy座標は
\Delta y_i \equiv f(x_{i+1}) - f(x_i) = f'(x_i)\Delta x + O(\Delta x^2)
だけ変化します。
区間iでの曲線の長さを\l_i$とすると、三平方の定理から
\begin{aligned}
l_i &= \sqrt{\Delta x^2 + \Delta y_i^2}\\
&= \Delta x\sqrt{1 + \left(\frac{\Delta y_i}{\Delta x}\right)^2}\\
&\sim \Delta x \sqrt{1 + f'(x_i)^2}
\end{aligned}
です。また、スタート地点では速度が0であったとすると、エネルギー保存則から常に
が成り立ちます。ここから、区間iにおける速度v_iは
となります。区間iを走破するのにかかる時間T_iは
T_i = \frac{l_i}{v_i} = \frac{\sqrt{1+ f'(x_i)^2}}{\sqrt{2g f(x_i)}} \Delta x
です。かかる時間の総和Tは
T= \sum_i^N T_i = \sum_i^N T_i = \frac{l_i}{v_i} = \frac{\sqrt{1+ f'(x_i)^2}}{\sqrt{2g f(x_i)}} \Delta x
連続極限をとると、
T = \int_0^{x_\mathrm{f}} \frac{\sqrt{1+ f'(x)^2}}{\sqrt{2g f(x)}} dx
と積分の形になります。ただし、x_\mathrm{f}は終点のx座標です。これを最小にするようなf(x)を求めなさい、というのが最速降下曲線問題です。
変分法
先ほどの式は、関数f(x)を与えると、スカラー値Tが決まります。このように「関数を決めるとスカラー値が決まる」ような関数(写像)を汎関数と呼び、T[f]と書きます。関数f(x)とその微分f'(x)に依存する関数の関数F(f(x),f'(x))を考えます。そして、始点x_\mathrm{i}と終点x_\mathrm{f}を固定して、以下のような汎関数を考えます。
T[f] = \int_{x_\mathrm{i}}^{x_\mathrm{f}} F(f,f') dx
本稿では証明しませんが、汎関数微分により、T[f]を最小(正しくは停留)とするようなfは、以下のオイラー・ラグランジュの式を満たす必要があることがわかります。
\frac{d}{dx} \left(\frac{\partial F}{\partial f'}\right) - \frac{\partial F}{\partial f} = 0
さらに、F(f, f')がxに陽に依存しない場合、すなわち
\frac{\partial F}{\partial x}=0
が成り立つ時には、ベルトラミの公式
F - f' \frac{\partial F}{\partial f} = C
が使えます。Cは定数です。ここに、
F(f(x),f'(x)) = \frac{\sqrt{1+ f'(x)^2}}{\sqrt{2g f(x)}}
を代入して整理すると、最終的に
\frac{df}{dx} = \sqrt{\frac{2a -f}{f}}
という形になります。ただし2a = 1/(2gC^2)です。
この微分方程式に、先程の媒介変数表示された解、
\begin{aligned}
x &= a (s - \sin \phi), \\
y &= a (1 - \cos \phi).
\end{aligned}
を代入すると、確かに微分方程式を満たすことがわかります。定数aは境界条件から決まります。これが変分法による解法です。
スネルの法則
さて、最速降下曲線の問題がスネルの法則の連続版であることを見る前に、スネルの法則を導いておきましょう。
A地点からB地点まで最速で行きたいとします。ただし、A地点のある領域を歩く速度はv_Aであり、B地点のある領域の速度はv_Bであるとします。ここで、領域の界面が平坦であり、かつv_A > v_Bであるとしましょう。A側の領域を歩く速度の方が速いので、なるべくA側で距離を稼ぐ方が得です。しかし、あまりA側を歩きすぎると全体の距離が長くなり、速度が速いというメリットが損なわれます。どこかにちょうど良い場所があるはずです。
同じ領域内では最速の軌跡は直線ですから、A 地点から界面上の点Xまで直線的に、また点XからB地点まで直線的に移動するのが最短経路となるでしょう。したがって、この問題は界面上のどこに点Xを取るか、という問題になります。
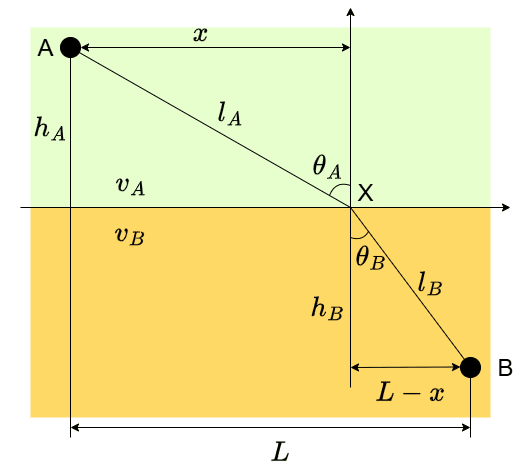
A地点からB地点の水平方向の距離をLとしましょう。また、A、Bから界面への距離をそれぞれh_A、h_Bとします。Aから界面上の点Xまでの水平方向の距離をxとします。すると、BからXまでの水平方向の距離はL-xです。あとのために、図のように界面に垂直な線から軌道までの角度\theta_A, \theta_Bを定義しておきます。
ここから、AからXまでの距離l_A、BからXまでの距離l_Bはそれぞれ以下のように決まります。
\begin{aligned}
l_A &= \sqrt{x^2 + h_A^2} \\
l_B &= \sqrt{(L-x)^2 + h_B^2}
\end{aligned}
A側を通過する時間をT_A(x)、B側を通過する時間をT_B(x)とすると、それぞれ
T_A(x) = \frac{l_A}{v_A}, T_B(x) = \frac{l_B}{v_B},
ですから、トータルの時間T(x) = T_A(x) + T_B(x)は
T(x) = \frac{\sqrt{x^2 + h_A^2}}{v_A} + \frac{\sqrt{(L-x)^2 + h_B^2}}{v_B}
これを最小とするxはT'(x)=0を満たすはずなので
\begin{aligned}
T'(x) &= \frac{x}{v_A \sqrt{x^2 + h_A^2}} - \frac{L-X}{v_B \sqrt{(L-x)^2 + h_B^2}} \\
&= \frac{x}{l_A v_A} - \frac{L-x}{l_B v_B}\\
&= \frac{\sin \theta_A}{v_A} - \frac{\sin \theta_B}{v_B} \\
&=0
\end{aligned}
つまり、
\frac{\sin \theta_A}{v_A} = \frac{\sin \theta_B}{v_B}
が成り立ちます。これは、スネルの法則に他なりません。
最速降下曲線
もう一度最速降下曲線について考えましょう。折れ線近似を考えます。

それぞれの区間は直線で進むとして、区間iにおける速度をv_i、次の区間への入射角を\theta_iとします。始点と終点を固定し、区間内は直線的に進むのであれば、最短経路をとるためにはスネルの法則を満たす必要があるため、先ほどの議論と全く同様に
\frac{\sin \theta_i}{v_i} = \frac{\sin \theta_{i+1}}{v_{i+1}}
が成り立っていることが期待されます。連続極限を取ると、
\frac{\sin \theta(x)}{v(x)} = C
となります。これがスネルの法則の連続版です。ただし、\theta(x)とv(x)は、水平位置位置xにおける入射角と速度です。
位置xにおける高さはf(x)ですから、エネルギー保存則から
となります。これとスネルの法則連続版からv(x)を消去してf(x)について解くと、
\begin{aligned}
f(x) &= \frac{v^2}{2g} \\
&= \frac{\sin^2 \theta}{2gC^2} \\
&= 2a \sin^2 \theta\\
&= a (1 - \cos 2\theta)
\end{aligned}
ただし、2a = 1/(2gC^2)で、途中で倍角公式を使いました。
また、図の傾きの定義から
\frac{df}{dx} = \tan \left(\frac{\pi}{2} - \theta \right) = \frac{\cos \theta}{\sin \theta}
であることがわかるので、
\begin{aligned}
\frac{dx}{d\theta} &= \frac{dx}{df} \frac{df}{d\theta} \\
&= \frac{\sin \theta}{\cos \theta} \frac{d}{d\theta} \left(2a \sin^2 \theta \right) \\
&= \frac{\sin \theta}{\cos \theta} (4a \sin \theta \cos \theta)\\
&= 4a \sin^2 \theta
\end{aligned}
初期条件としてx(0) = 0を採用して積分すると
x = 2a \left(\theta - \frac{1}{2}\sin2\theta \right)
以上をまとめると、
\begin{aligned}
x &= 2a \left(\theta - \frac{1}{2}\sin2\theta \right)\\
y &= f(x) = a (1 - \cos 2\theta)
\end{aligned}
ここで、\phi = 2 \thetaとすると、
\begin{aligned}
x &= a \left(\phi - \sin \phi \right)\\
y &= a (1 - \cos \phi)
\end{aligned}
これが求めたかったサイクロイド曲線でした。
まとめ
スネルの法則とは、速度一定の区間が接する領域で最速のルートを選ぶ時に現れる速度と入射角の関係であり、最速降下曲線問題はスネルの法則の連続版であることを見ました。「なぜ最速降下曲線の問題に媒介変数として角度が現れるのか?」という問いには、「最速降下曲線はスネルの法則の連続極限とみなすことができるから。」と答えることができます。
最速降下曲線問題は変分原理の最も有名な例であるわりに、その幾何学的な意味はあまり深入りしないことが多い気がしたので、少し詳細に説明してみました。
なお、スネルの法則の入射角\thetaとサイクロイドの回転角\phiになぜ二倍の関係があるか、についても幾何学的な証明を与えることができますが、ここでは省略します。気になる人は考えてみると良いでしょう。






Discussion