制限ボルツマンマシンの基礎 ～推定編～

はじめに

機械学習で用いられるボルツマンマシン、特に制限ボルツマンマシン(Restricted Boltzmann Machine, RBM)の解説その2です。その1の続きなので、そちらを見てから読んでください。

前回までのあらすじ

ぼっち飯のDaveは、いつも学食前のテラスでお弁当を食べていますが、同じクラスのAliceとBobが学食をよく利用していることに気づきます。しかし、AliceとBobは同時に現れることは少ないようです。AliceとBobは仲が悪いのでしょうか？

そこでDaveは239日にわたって二人を観察し、AliceとBobが学食に来た日、来ていない日の統計を取りました。

A	B	日数
x	x	35
x	o	56
o	x	113
o	o	35

Daveは、この結果を説明するモデルを作ることにしました。これは、ぼっち飯のDaveによるAliceとBobの調査研究の物語です。

確率モデルと最尤推定

Daveがやろうとしているのは、観測事実をもっともよく説明するモデルを作ることです。しかし、「観測事実をもっともよく説明をするモデルを作る」というのは、わりと非自明なことです。

例えばいま、コインを4回投げて、「裏、裏、裏、表」という順番になったとします。このコインの振る舞いを最もよく説明するモデルとはどういうモデルでしょうか？

一番素直なモデルは、「このコインは裏と表が等しい確率で、裏表が毎回独立に出る」と考えることです。つまり、普通の公平なコインということです。その場合、4回投げたら、表が2回出る確率が一番高いですが、表が1度しか出ない確率もさほど低くはありません。

次に、「このコインは、表が出る確率が1/4、裏が出る確率が3/4で、裏表が毎回独立に出る」と考えることもできます。この場合、「4回投げて表が1度しか出ない」確率は、公平なコインよりも高くなります。

もっと極端に、「このコインは機械仕掛けになっており、投げるたびに裏→裏→裏→表→裏→裏→裏→表……と出る」と考えることもできます。この場合は、「裏、裏、裏、表」と出る確率は100%なので、この「モデル」が一番事象を説明している、と言えなくもありません。

完全にランダムと、完全に決定論的の中間で、「このコインは、一度裏が出たら次も裏が出やすい」というモデルを考えることもできます。例えば、次に4回投げて「表、表、表、裏」などが出たら、この説が有力になりますね。これは試行間に相関があると仮定したモデルになります。

以上のように、「コインを4回投げたら裏、裏、裏、表になった」という観測事実を「説明」するモデルは無数に作ることができます。ここでは

• 試行間に相関がない(無相関)
• 表と裏が出る確率が偏っている

という二つを仮定したモデルを考えることにしましょう。表が出る確率を$p$、裏が出る確率を$1-p$とします。試行間に相関がないことを仮定したので、表と裏が出る順番には意味がありません。すると、「4回投げたら裏が3回出た」という観測事実を最もよく説明するように$p$を決めましょう、という問題に落ちます。

確率$p$で表が出る独立な試行は二項分布に従うので、4回のうち1度だけ表が出る確率$P$は

$$P(p) = 4p(1-p)^3$$

です。これを最大にするような$p$を知りたいので、$p$で微分しましょう。

$$\begin{aligned} P'(p) &= 4(1-p)^3 - 12(1-p)^2 \\ &= 4(1-p)^2(1 - 4p) \end{aligned}$$

$P'(p) = 0$より、$p=0, 1/4$と求まります。このうち、$P(p)$が$0\leq p\leq 1$で最大値を取るのは$p=1/4$です。要するに、表が出る確率$p$が$1/2$ではない不公平なコインを$N$回投げて、表が$n$回出た時、表が出る確率を$p=n/N$と推定しましょう、という至極当たり前なことを言っています。

このように、まずモデルを仮定し、その上で観測事実をもっともうまく説明できるようにモデルパラメータを決める手法を最尤推定といいます^[1]。

ボルツマンマシンに現れる変数が二値であることから、後に現れる最尤推定は基本的に全て不公平なコインと同じものになります。

独立モデル

さて、Daveはモデルを作るために統計表を眺めます。

A	B	日数
x	x	35
x	o	56
o	x	113
o	o	35

Aliceが学食に来たかどうかを表す変数を$v_a$とします。$v_a=1$ならAliceが学食に来たことを、$v_a=0$なら来ていないことを表します。Bobを表す変数$v_b$も同様です。

まず、観測日数239日のうち、Aliceが学食に来たのは148日、来なかった日は91日でした。したがって、

$$P(v_a = 1) = \frac{148}{239}, P(v_a = 0) = \frac{91}{239}$$

です。同様に、Bobが学食に来たのは91日、来なかったのは148日なので、

$$P(v_b = 1) = \frac{91}{239}, P(v_b = 0) = \frac{148}{239}$$

と表せます。さて、AliceとBobが学食に来る確率が全く独立であると仮定してみましょう。すると、AliceとBobが同時に現れる確率は、それぞれ個別の確率の積になるので(確率における独立の定義)

$$P(v_a=1, v_b=1) = P(v_a = 1) P(v_b = 1) = \frac{148\cdot 91}{239^2}$$

となります。239日にわたって観測したとすると、二人が同時に現れる日数は$148\cdot 91 / 239 \sim 56.4$日と推定できます。

同様に、残りの表も埋めてみましょう。

A	B	実際の日数	独立と仮定した時の日数
x	x	35	56.4
x	o	56	34.6
o	x	113	91.6
o	o	35	56.4

Daveはこの表を見て、AliceとBobが学食に来る確率は独立ではないと推定することにしました。特に、両方とも学食に来る確率が、独立モデルによる推定よりも低いため、AliceとBobは仲が悪いことが推定されます。

ボルツマンマシン

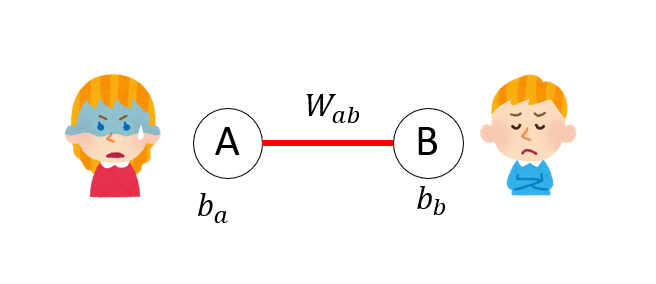
次にDaveは、「AliceとBobが仲が悪い」ことを表すモデルを作ることにしました。Daveは、ちょうど大学で学んだボルツマンマシンというモデルを応用することにします。ボルツマンマシンは、1か0を取る変数の実現確率が、外場のあるイジング模型のようなエネルギーで表されるモデルです。AliceとBobの状態を表す変数を$v_a$,$v_b$として、ハミルトニアン(エネルギー)を

$$H(v_a, v_b) = - b_a v_a - b_b v_b - W_{ab} v_a v_b$$

と定義します。ここで$b_a$、$b_b$は前の記事で定義したバイアス、$W_{ab}$は相互作用です。負符号をつけているのは、「パラメータの値が大きいほど、変数が$1$を取りやすい」ことを表現するためです。

ある状態$(v_a, v_b)$の出現確率$P(v_a, v_b)$は

$$P(v_a, v_b) = \frac{\exp(-H(v_a, v_b))}{Z}$$

というボルツマン重みで表現されます。ただし$Z$は分配関数で、具体的な表記は

$$Z = \sum_{v_a}^{0,1}\sum_{v_a}^{0,1} \exp(-H(v_a, v_b))$$

で与えられます。

まずはAliceのバイアス$b_a$を決めましょう。このバイアスは、他に条件がない場合にどれだけ変数$v_a$が$1$になりやすいかを決めるパラメータで、今回の場合はBobが来ていないという条件でAliceが学食にどれだけ来やすいかを表しています。正なら学食に来やすい、負ならあまり来ないことになります。

A	B	日数
x	x	35
o	x	113

表を見ると、Bobが来なかったのは148日、そのうちAliceが学食に現れたのは113日です。Bobが来ない時にAliceが来る確率を$p$として、この確率をボルツマンマシンで表現しましょう。

AliceもBobも学食に来ない場合、エネルギーがゼロになるので、

$$1 - p = P(v_a =0 | v_b=0) = \frac{1}{\tilde{Z}}$$

一方、Aliceだけ学食に来る場合の確率は

$$p = P(v_a =1 | v_b=0) = \frac{\exp(b_a)}{\tilde{Z}}$$

です。ただし、

$$\tilde{Z} = 1 + \exp(b_a)$$

です。

すると、先ほど見た「不公平なコインにおける最尤推定」と全く同じ状況になっています。表が出る(Aliceが来る)確率が$p$、裏が出る(Aliceが来ない)確率が$1-p$のコインを148回投げたら、表が出た(Aliceが来た)回数が113回になったのですから、この観測事実を最も良く説明する$p$は

$$p = \frac{113}{148}$$

です。

以上から、

$$\exp(b_a) = \frac{113}{35}$$

と推定できます。他のパラメータも同様に決められますが、どうせ全て指数関数の肩に乗った形で出てくるので、以下のように略記することにしましょう。

$$\begin{aligned} \exp(b_a) &\equiv w_a\\ \exp(b_b) &\equiv w_b\\ \exp(W_{ab}) &\equiv w_{ab}\\ \end{aligned}$$

「Aliceが来ていない時のBobの来やすさ」を表すバイアス$b_b$に関しても、同様な表を作って計算できます。

A	B	日数
x	x	35
x	o	56

ここからただちに

$$w_b \equiv \exp(b_b) = \frac{56}{35}$$

と推定できます。

さて、次に相互作用$W_{ab}$を推定しましょう。AliceとBobは仲が悪い(と、ぼっちのDaveは思っている)ため、$W_{ab}<0$であることが予想されます。

Bobが来ているという条件で、Aliceの出現確率を調べます。

A	B	日数
x	o	56
o	o	35

Bobが来たという条件で、Aliceが来こなかったのは56日、来たのは35日です。Bobが来たという条件では、エネルギーは

$$\begin{aligned} H(v_a , v_b=1) &= b_a v_a + b_b + W_{ab} v_a \\ &= (b_a + W_{ab}) v_a + b_b \end{aligned}$$

ここで、$b_b$の項は、エネルギーの基準を決めているだけなので無視できます。すると、先ほど「Bobが来なかった時」にAliceのバイアスを決めたのと全く同様な議論ができます。

$v_a=0$の時には重みが1、$v_a=1$の時には重みが$w_a w_{ab}$になり、Aliceが学食に来なかった日数と来た日数の比が$56:35$なのですから、

$$56:35 = 1 : w_a w_{ab}$$

です。$w_a = 113/35$でしたから、

$$w_{ab} = \frac{35^2}{113\cdot 56}$$

です^[2]。$w_{ab} < 1$であることから、予想通り$W_{ab} < 0$であることがわかります。

これで全てのパラメータが決まりましたが、念のため「Aliceが来ている」という条件でBobが来なかった日、来た日の日数が正しく推定されるか確認してみましょう。

Aliceが来ているということから$v_a=1$です。この時、エネルギーは

$$H(v_a =1, v_b) = -(b_b + W_{ab})v_b - b_a$$

となります。$b_a$は無視できるため、結局Bobが来ない日のボルツマン重みは1、Bobが来る日のボルツマン重みが$w_b w_{ab}$となります。

先ほどと全く同様な議論から、このボルツマンマシンはAliceが来ているという条件下でBobが学食に来ない日と来る日の日数の比を$1 : w_b w_{ab}$と予想します。

$$\begin{aligned} w_b &= \frac{56}{35} \\ w_{ab} &= \frac{35^2}{113\cdot 56} \end{aligned}$$

でしたから、「Aliceが来ている」という条件で、Bobが来ない日数と来る日数の比は$1:35/113$と予想されます。

見てみましょう。

A	B	日数
o	x	113
o	o	35

Aliceが学食に来た日のうち、Bobが学食に来なかったのが113日、来た日が35日ですから、確かに比が$113:35 = 1: 35/113$になっており、このモデルは観測事実を説明できています。

Daveが構築したモデルは、以下のハミルトニアンで表されるボルツマンマシンです。

$$H(v_a, v_b) = - b_a v_a - b_b v_b - W_{ab} v_a v_b$$

パラメータは以下のように決定できました。^[3]

$$\begin{aligned} \exp(b_a) &\equiv w_a = \frac{113}{35}\\ \exp(b_b) &\equiv w_b = \frac{56}{35}\\ \exp(W_{ab}) &\equiv w_{ab} = \frac{35^2}{113\cdot 56}\\ \end{aligned}$$

各パラメータ$b_a$,$b_b$、$W_{ab}$は、「正ならその状態を好み、負ならその状態を嫌がる」という意味を持っています。

それらを指数関数の肩に載せた$w_a, w_b, w_{ab}$は、「1より大きければその状態を好み、小さければその状態を嫌がる」ことになります。いま、バイアスが1より大きい$(w_a, w_b > 1)$ことから、お互いが学食にいなければ学食に出現しやすく、相互作用が1より小さい$(w_{ab} < 1)$ことから、「両方が学食に来るのは嫌がる」ことが表現されています。どうやらそれっぽいモデルができました。

制限ボルツマンマシン

モデルの構築

ぼっちのDaveは、AliceとBobが学食に現れる確率モデルを構築することができて満足です。しかしある時、クラスの飲み会でそれとなくAliceとBobの仲を聞いたところ「名前は知っているくらいで、特にお互い好きでも嫌いでもない」ということが分かって愕然としました。モデルを作り直さなければなりません。

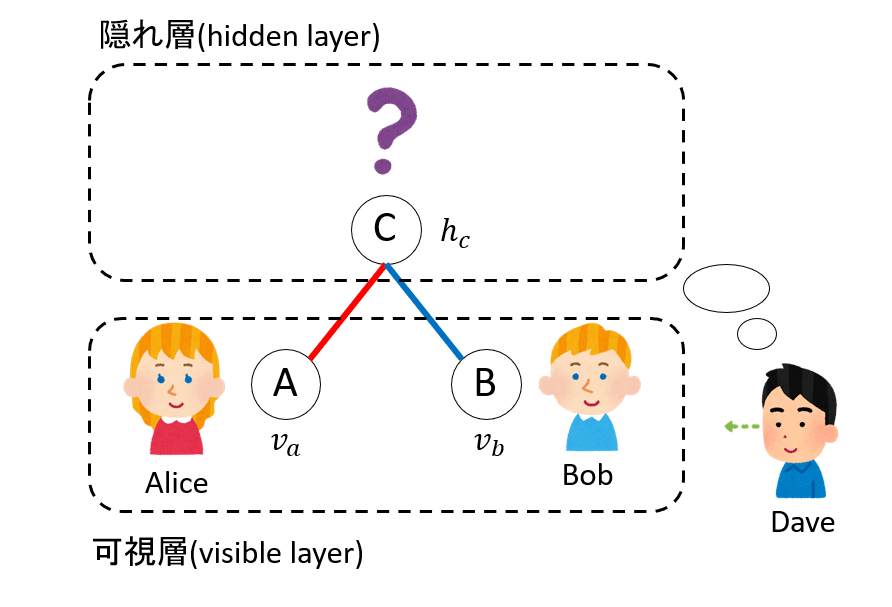
AliceとBobには直接相互作用がないので、モデルでもそこに線は引けません。そこでDaveは、隠れた変数$h_c$を導入することにします。$h_c$は、Daveからは見えないけれど、何か(カレーフェア)が起きているか起きていないかを表す変数です。この変数を通じて、AliceとBobが間接的に相互作用をします。

ハミルトニアンはこうなります。

$$H(v_a, v_b, h_c) = -(b_a v_a+ b_b v_b+ b_c h_c + W_{ac}v_a h_c + W_{bc}v_b h_c)$$

AliceとBobの直接相互作用を表す重み$W_{ab}$を消した変わりに、隠れ変数との相互作用を表す重み$W_{ac}$と$W_{bc}$が導入されました。

このモデルは、二値変数の実現確率がボルツマン重みに従うというボルツマンマシンの一種ですが、同じグループ内は相互作用がないように変数を二つのグループに分けることができるので、制限ボルツマンマシン(restricted boltzmann machine, RBM) になっています。

まずわかることは、パラメータが5個(バイアス3個、重み2個)もあるのに、観測事実が4種類しかないため、パラメータを一意に決めることができません^[4]。どこかでえいやと決める必要がありそうです。

パラメータの決定

とにかく、ありそうな状態のボルツマン重みを決めていきましょう。状態$(v_a, v_b, h_c)$に対するボルツマン重みを$\omega(v_a, v_b, h_c)$とします。ここで

$$\omega(v_a, v_b, h_c) = \exp(-H(v_a, v_b, h_c))$$

です。隠れ変数$h_c$はDaveから見えないので、Daveからは$h_c$について和をとった事象のみ観測可能です。この時の重みを$\omega(v_a, v_b)$で表しましょう。

$$\omega(v_a, v_b) = \omega(v_a, v_b, h_c=0)+\omega(v_a, v_b, h_c=1)$$

です。

さて、AliceもBobも学食に来ていないという事象のボルツマン重みを計算しましょう。

$$\omega(v_a=0, v_b=0) = \omega(v_a=0, v_b=0, h_c=0)+\omega(v_a=0, v_b=0, h_c=1)$$

であり、

$$\begin{aligned} \omega(v_a=0, v_b=0, h_c=0) &= 1 \\ \omega(v_a=0, v_b=0, h_c=1) &= w_c \\ \end{aligned}$$

であることから、

$$\omega(v_a=0, v_b=0) = 1 + w_c$$

です。ここで

$$w_c \equiv \exp(b_c)$$

です。今後、$w_{ac}$や$w_{bc}$も同様に定義することにします。

同様に、Bobが学食に来ておらず、Aliceが来ているという事象のボルツマン重みはこうなります。

$$\omega(v_a=1, v_b=0) = w_a + w_a w_c w_{ac}$$

逆に、Aliceが学食に来ておらず、Bobが来ているという事象のボルツマン重みは以下の通りです。

$$\omega(v_a=0, v_b=1) = w_b + w_b w_c w_{bc}$$

最後に、AliceもBobも学食に来ているという事象のボルツマン重みは以下のようになります。

$$\omega(v_a=1, v_b=1) = w_a w_b + w_a w_b w_c w_{ac} w_{bc}$$

以上を表にまとめましょう。

A	B	日数	重み
x	x	35	$1 + w_c$
x	o	56	$w_b + w_b w_c w_{bc}$
o	x	113	$w_a + w_a w_c w_{ac}$
o	o	35	$w_a w_b + w_a w_b w_c w_{ac} w_{bc}$

重みと事象の発生頻度は比例するはずなので、日数の比と矛盾しないようにパラメータを決めなさい、という問題になります。しかし、観測事実の自由度は3であり、パラメータが5つもあるのでこのままでは決まりません。

そこでDaveは、一番簡単な「AliceもBobも学食に来ていない」という事象に注目します。重みと日数は比例するので、比例係数を$a$とすると

$$a (1 + w_c) = 35$$

です。他に、56や35といった、7の倍数があるので、$a=7$に取るのが良さそうです。ここから

$$(1 + w_c) = 5$$

となり、

$$w_c = 4$$

と求まります。

次に、AliceもBobも学食に来ているという重みに注目します。比例係数を考慮すると、

$$w_a w_b + w_a w_b w_c w_{ac} w_{bc} = 5$$

です。$w_c=4$を代入して整理すると

$$w_a w_b(1 + 4 w_{ac} w_{bc}) = 5$$

です。ここで$w_{ac}$は隠れ事象とAliceの相互作用の重み、$w_{bc}$は隠れ事象とBobの相互作用の重みです。AliceとBobは同時には現れにくいのですから、どちらかが1より大きく、どちらかが1より小さいはずです。Daveは、えいやと

$$w_{ac} w_{bc} = 1$$

を仮定しました。すると先ほどの式から

$$w_a w_b = 1$$

となります。

残りの二つの「Bobが来てAliceが来ない」事象と、「Aliceが来てBobがこない」事象の重みと日数の関係から

$$\begin{aligned} w_b(1+4w_{bc}) &= 8 \\ w_a(1+4w_{ac}) &= \frac{113}{7} \\ \end{aligned}$$

両辺を辺々かけて$w_a w_b = 1$であることを使うと

$$(1+4w_{bc})(1+4w_{ac}) = \frac{8\cdot 113}{7}$$

$w_{bc} = 1/w_{ac}$であることから、$w_{bc}$を消去すると、これは二次方程式になるので解けて

$$w_{ac} = 28, \frac{1}{28}$$

ここで、$w_{ac} = 28$を採用すれば

$$w_{bc} = \frac{1}{28}$$

となります。これを、先ほどの

$$\begin{aligned} w_b(1+4w_{bc}) &= 8 \\ w_a(1+4w_{ac}) &= \frac{113}{7} \\ \end{aligned}$$

に代入すれば

$$\begin{aligned} w_a &= \frac{1}{7} \\ w_b &= 7 \end{aligned}$$

となり、全ての重みが求まりました。求められた重みを全て整理すると

$$\begin{aligned} w_a &= \frac{1}{7} \\ w_b &= 7 \\ w_c &= 4 \\ w_{ac} &= 28 \\ w_{bc} &= \frac{1}{28} \\ \end{aligned}$$

念のため、先ほどの表に値を代入しておきましょう。

A	B	日数	重み	重みの値
x	x	35	$1 + w_c$	5
x	o	56	$w_b + w_b w_c w_{bc}$	8
o	x	113	$w_a + w_a w_c w_{ac}$	113/7
o	o	35	$w_a w_b + w_a w_b w_c w_{ac} w_{bc}$	5

確かに重みの値が日数(観測事実)と比例しており、このモデルが観測事実を説明できていることがわかります。

モデルの考察

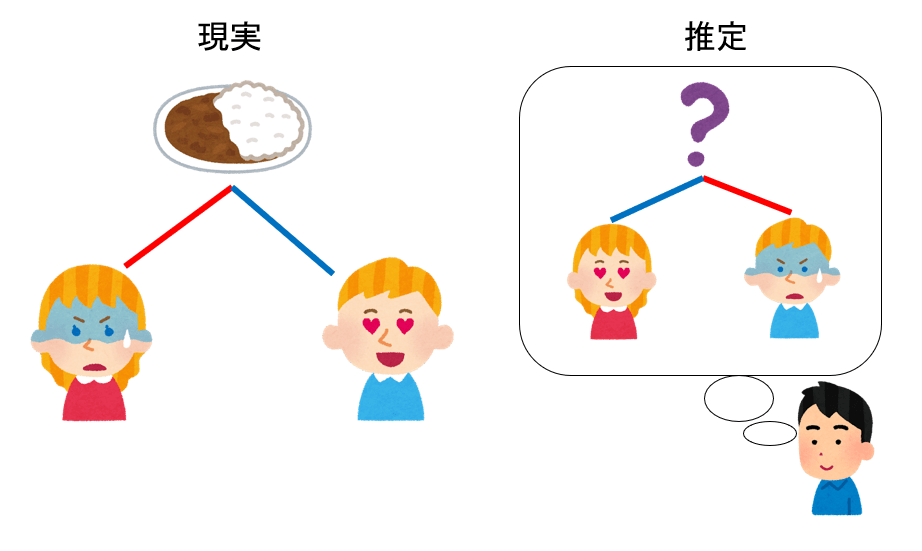
さて、Daveはこのパラメータから、「裏で起きていること」を考察します。隠れ変数$h_c$が示す事象を「イベントX」と呼ぶことにしました。

バイアスが$w_c = 4$と大きいことから、学食ではイベントXが頻繁に起きていることが推定されます。

Aliceのバイアス$w_a$が小さいのに対して、イベントXとの相互作用$w_{ac}$が非常に大きいので、Aliceは「学食で起きているイベントXが大好きで、そのイベントがなければ学食には来ないが、そのイベントが起きたら極めて高確率で学食に来る」ことが推定されます。

逆に、Bobのバイアスは大きいのに対して、イベントXとの相互作用はかなり小さいため、BobはイベントXを嫌っていることが推定されます。

以上から、Daveは以下のような推論をしました。

• 学食では 頻繁に イベントXが起きている
• AliceはイベントXが 大好き で、そのイベントが起きたら学食に高確率で現れる
• BobはイベントXが 大嫌い で、そのイベントが起きたら学食には現れない

しかし、現実はこうでした。

• 学食では たまに カレーフェアが実施されている(239日中64日)
• Aliceはカレーフェアが 大嫌い で、そのフェアが実施されていたら学食には現れない
• Bobはカレーフェアが 大好き で、そのフェアが実施されていたら学食に高確率で現れる

すなわち、隠れ事象(カレーフェア)と、登場人物の好き嫌いを全く逆に推定してしまいました。これは、重みの正負を逆に推定したことを意味しています。

Daveから見える(visible)変数はAliceとBobだけなので、「AliceとBobが同時に現れない」という観測事実だけからは、隠れ事象との重みの符号は推定できません。しかし、「AliceとBobは、お互いには無関係だが、隠れ事象により間接的に相互作用し、同時に現れる確率が下がる」という事実までは正しく推定することができました。

まとめ

一部の事実を知らないDaveの気持ちになって、観測事実を説明するモデルを構築してみました。観測事実と無矛盾な結果を与えるモデルを作ることはできましたが、そのモデルによる「解釈」は、事実とは全く逆になってしまいました。「モデルが観測事実を説明するが、解釈は事実と異なる」というのは示唆的ですね。

ここでは、観測事実からモデルのパラメータを手で最尤推定しました。ボルツマンマシンとは、要するに「注目する要素以外の全ての条件を固定した場合、注目する事象が起きるか起きないかが二項分布に従う」というモデルです。そして、二項分布のパラメータ(成功確率)$p$が、他の条件に依存しています。従って、原理的には事象を固定して、「不公平なコイン」の確率を最尤推定する問題としてモデルパラメータを決定することができます。

しかし、一般的には観測事実もモデルパラメータも膨大であるため、一つ一つ決めることは不可能です。そこで、サンプリングによりパラメータを逐次更新していく方法を採用しますが、一般のボルツマンマシンの学習は困難です。しかし、制限ボルツマンマシンであれば、Contrastive Divergence法という効率の良い学習方法があるため、パラメータを比較的容易に決めることができます。

そのあたりは「制限ボルツマンマシンの基礎 ～学習編～」で(もし書けたら)触れます。

脚注

1. 最尤推定に限らず、確率まわりは用語の定義が面倒です。本稿ではそのあたりを適当に済ませるので、真面目に学びたい人は真面目な本を読んでください。

2. 分かりやすさのため、わざと約分していません。以下同様。

3. パラメータに表れる数字が、観測事実の日数であることに注意しましょう。

4. 実際には規格化条件があるので、使える観測事実は3種類。