🍗

(結論 : そこまで変わらない) GPT4o を使用した PDF の要約は画像だと圧倒的に安い?

2024/05/15に公開

OpenAI

LLM

GPT-4o

tech

概要

PDF を要約するサービスを開発しています(何番煎じ?).
通常論文の要約にはテキスト化を行って要約していますが,
大きな PDF ファイルを要約しようとするとトークン数が膨大になります.
GPT4 だとお金が結構かかっていたけど GPT4o になって画像認識の精度が上がったので比較してみました.
(outputは考慮していないです)

以下のポストを見て気になったのが発端

結論

値段としてはそこまで変わらないが表を考慮してくれたり古い論文の文字をうまくテキストにできないものなどに適している.
パワーポイントのスライドなどは文字数が少ないので画像のほうが値段は上がるので考えどころだが,
図を説明してくれるという点で画像を使用するのは良いと思う

テキスト
- GPT4 : $0.4698
- GPT4o : $0.007725
画像
- GPT4o : $0.005525

画像認識の精度について

PDFから画像にした論文の画像が以下のようなもののとき出力は結構いい感じに出ている.

入力画像

式を見てみるとおかしな部分はあるがテキストを要約した場合でも式は崩れてしまうがテキストでもある程度崩れるのでそこまで違いはないかと思う

元の式
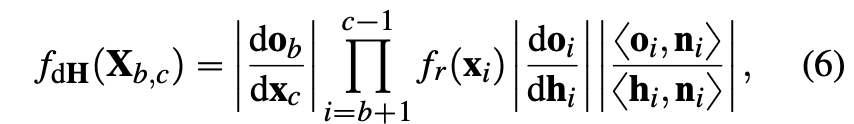
画像から生成
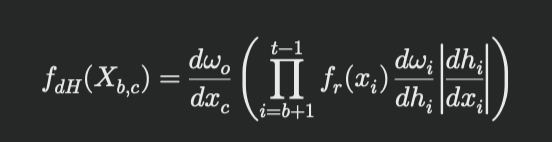
テキストから生成

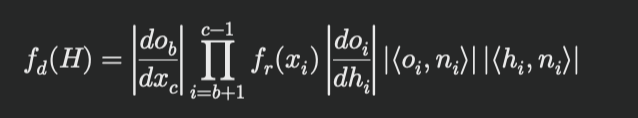
元の式
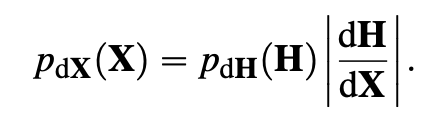
画像から生成
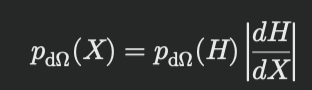
テキストから生成

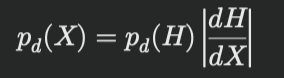
gpt4o の出力

このページでは、次の事象推定（NEE）と関連する測定と確率密度関数（PDF）計算の手法について詳しく説明しています。また、関連する数学的な式が提供されています。

アルゴリズム2: PDFの評価

アルゴリズム2の説明:

•	パスの接尾辞 ( x_b, x_c ) を要求し、 ( p_{\text{d}\Omega}(x_c) ) を返す。
•	( p_{\text{d}\Omega}(x_c) ) は光源上の点 ( x_c ) のPDFである。
•	( x_b ) から ( x_c ) までの直線上の頂点 ( y_{b, t+1} ) の集合を考える。
•	頂点が許容可能な位置にない場合、新しいパスを見つけるか、計算を終了する。

ハンドリングオクルージョン (Handling Occlusion)

図3では、NEEサンプル ( x_b ) が許容可能なパスの領域内でのみ光源を見つけることができることを示しており、自己オクルージョンを避けるためのトレランスマージンの処理方法について説明しています。

3.2. 半ベクトルのサンプリング (Sampling Half Vectors)

•	MLT文脈では、パス空間がよく探査されるが、Monte Carlo文脈では、半ベクトルの分布を非常に注意深くサンプリングする必要がある。
•	この手法では、BSDFの分布を使用し、グローバル分布からではなく、可視半ベクトルからサンプリングする。

3.3. 測定とPDFの計算 (Computing the Measurement and PDF)

測定の寄与とPDFの評価には、次の数式を使用します：

•	測定寄与関数 ( f(X) ) を評価し、半ベクトル空間におけるPDF ( p_{\text{d}\Omega}(H) ) とその比を評価します。

f_{d\Omega}(X) = \frac{f_{dH}(X)}{p_{\text{d}\Omega}(H)}

•	測定寄与関数は次のように定義されます：

f_{dH}(X_{b,c}) = \frac{d\omega_o}{dx_c} \left( \prod_{i=b+1}^{t-1} f_r(x_i) \frac{d\omega_i}{dh_i} \left| \frac{d h_i}{d x_i} \right| \right)

ここで、 ( \left| \frac{d h_i}{d x_i} \right| ) は半ベクトルの空間でのヤコビアンであり、反射方向 ( \omega_i ) からの変換を含みます。

•	次に、PDFの評価には、次の関係を使用します：

p_{\text{d}\Omega}(X) = p_{\text{d}\Omega}(H) \left| \frac{dH}{dX} \right|

ヤコビアンの評価には、三重対角行列のブロックを逆にするためにLU分解を使用します：

\left| \frac{d(h_{b+1}, \ldots, h_{t-1})}{d(x_{b+1}, \ldots, x_{t-1})} \right| = \prod_{i=b}^{t-1} \Lambda_i

ここで、 ( \Lambda_i ) はLU分解の過程で計算される値です。

スペキュラケース (Specular Case):

•	スペキュラケースでは、半ベクトル  h_i  をサンプリングし、デルタハーフ空間を考慮してBSDF評価を行います。

数式

•	測定寄与関数：

f_{dH}(X_{b,c}) = \frac{d\omega_o}{dx_c} \left( \prod_{i=b+1}^{t-1} f_r(x_i) \frac{d\omega_i}{dh_i} \left| \frac{d h_i}{d x_i} \right| \right)

•	PDFの評価：

p_{\text{d}\Omega}(X) = p_{\text{d}\Omega}(H) \left| \frac{dH}{dX} \right|

•	ヤコビアンの評価：

\left| \frac{d(h_{b+1}, \ldots, h_{t-1})}{d(x_{b+1}, \ldots, x_{t-1})} \right| = \prod_{i=b}^{t-1} \Lambda_i

値段の比較

それぞれ要約を実施したときの価格を比較してみると

画像の要約の場合

画像あたりの価格

GPT4 : $0.011049
GPT4o : $0.005525

テキストでの要約の場合

PDF をテキストにして以下のサイトでトークン数を計算すると

文字数: 4747
GPT-4 (cl100k_base) tokens: 1566
GPT-4o (o200k_base) tokens: 1545, (1.34 % ダウン)

gpt-4o
input : $5.00 / 1M tokens
output : $15.00 / 1M tokens

gpt-4
input : $30.00 1M tokens
output : $60.00 1M tokens

価格は
GPT4 : $0.4698
GPT4o : $0.007725

PDF をテキストにしたもの

J. Hanika & M. Droske & L. Fascione / Manifold Next Event Estimation
Algorithm 2 PDF evaluation.
Require: path sufﬁx Xb,c return PDF pdxpXb,cq
pdxpxcq Ð PDF of point xc on light source
Yb1,c´1 Ð vertices on straight line pxb,xcq // Sec. 3.1 pdHpHq Ð PDF of half vectors on input path X1 b1,c´1 Ð h_to_positionspHb1,c´1,Yq // Sec. 3.4 if |Xb1,c´1 ´X1
b1,c´1| ą ε then return 0 // fail: found a different path end if pdXpXb1,c´1q Ð pdHpHq¨
ˇ
ˇ
ˇ dphb1..hc´1q dpxb1..xc´1q
ˇ
ˇ
ˇ
// Sec. 3.3
return pdXpXb1,c´1q¨ pdxpxcq xa“0 x3 x1 xc“k xb“2 Figure 3: Handling occlusion: normal culling used with MNEE to sample xc needs special care not to cull light sources which are only visible for the admissible path (culling region for xb indicated in orange). Also, the seed path (dashed in orange) may be occluded, while the admis- sible path is not. For this reason, self-occlusion is checked only after determining the admissible positions of Xb1,c´1.
an additional tolerance margin to handle the conﬁguration
in this ﬁgure. Second, the seed path might be blocked by a
heavily displaced surface. We detect such cases and ignore
self-occlusion until the solver has converged and the admis-
sible positions of Xb1,c´1 are known. General occluders such as additional objects under the water droplet in our ex- ample are not a common use case for us, but ignoring them has a big impact on performance as it causes the Newton solver to run on paths that will in many cases still be oc- cluded after convergence, wasting computation. 3.2. Sampling Half Vectors Sampling is performed in the half vector domain, i.e. we know pdHpHq. In the MLT context, the path space is ex- plored well given an approximate step size proposal, e.g. chosen by assuming the half vector distribution of a surface point is Gaussian [KHD14a]. In contrast to that, in a pure Monte Carlo context it is imperative to sample the half vector distribution of the underlying BSDF very carefully. A good option is to use the sampling function of the BSDF, assum- ing that it draws from a global distribution and not from the visible normals [HD14]. This is because after the walk has converged, the incoming direction will be different from the one the half vector was sampled with, which will typically change the set of visible normals. 3.3. Computing the Measurement and PDF To evaluate the pixel contribution of a sampled path we need to evaluate the value of the Monte Carlo estimator, which is the ratio of the measurement contribution to the PDF (both in product vertex area measure) ˆ I “ fpXq{pdXpXq. To improve numerical stability in the evaluation of the measurement, we compute ˆ I “ fdHpXq{pdHpHq in half vector space [KHD14a, Eq. (4) and (5)] as this formulation contains no geometry terms for the sub-path Xb1,c:
fdHpXb,cq “
ˇ
ˇ
ˇ
ˇ
dob
dxc
ˇ
ˇ
ˇ
ˇ
c´1
ź
i“b1 frpxiq ˇ ˇ ˇ ˇ doi dhi ˇ ˇ ˇ ˇ ˇ ˇ ˇ ˇ xoi,niy xhi,niy ˇ ˇ ˇ ˇ, (6) where |doi{dhi| is well known from microfacet the- ory [WMLT07], i.e. 4|xoi,hiy| for reﬂections. Computing ˇ ˇdob{dxc ˇ ˇ “ Gpxb,xb1q|Tb1| via the determinant of the transfer matrix Tb1 pushes the accuracy limits of single-
precision ﬂoating point arithmetic: double precision or a
careful eye to implementation and compiler optimization pa-
rameters are recommended here.
Computing the PDF for MIS requires us to convert the
half vector PDF to product vertex area measure
pdXpXq “ pdHpHq
ˇ
ˇ
ˇ
ˇ
dH
dX
ˇ
ˇ
ˇ
ˇ.
(7)
The
routine
solve_matrix_h_to_x,
as
outlined
in [KHD14b, Fig. 2], inverts the block-tridiagonal constraint
derivative matrix with the blocks A,B,C for every vertex.
We use the same LU decomposition, and the full Jacobian
determinant
ˇ
ˇdH{dX
ˇ
ˇ can be computed very cheaply
inside this routine. More precisely, we evaluate
ˇ
ˇdH{dX
ˇ
ˇ
during the ﬁrst LU decomposition step as a product of
determinants [Mol07]:
ˇ
ˇ
ˇ
ˇ
ˇ
dphb1..hc´1q dpxb1..xc´1q
ˇ
ˇ
ˇ
ˇ
ˇ “
c´1
ź
i“b
|Λi|,
(8)
where the difference to the original code listing [KHD14b] is
that our index i runs over the sub-path i P rb,c´1s instead of
the whole path r0,k´1s. In order to reduce numerical issues,
it is worth computing this product in double precision.
Specular Case In the specular case, we sample the half vec-
tors with Dirac deltas pdhphiq “ δdhphiq. When evaluating
the pixel contribution ˆ
I, these deltas cancel with the mea-
surement contribution. In our implementation, the BSDF
evaluation returns the BSDF in delta-half vector space (in-
stead of the regular space of outgoing directions do). That
is, a specular dielectric will return κ (the Fresnel term R for
reﬂection). This avoids computing the per-vertex Jacobian in
c
⃝2015 The Author(s)
Computer Graphics Forum c
⃝2015 The Eurographics Association and John Wiley & Sons Ltd.
91

(結論 : そこまで変わらない) GPT4o を使用した PDF の要約は画像だと圧倒的に安い?

概要

結論

画像認識の精度について

値段の比較

画像の要約の場合

テキストでの要約の場合

参考

Discussion