U-Net: Convolutional Networks for Biomedical Image Segmentation

Introduction

画像タスクの中でセグメンテーションタスは、ピクセル単位でクラス分類などの予測を行うものです。大きく分けて

• セマンティックセグメンテーション
• インスタンスセグメンテーション
• パプノプティックセグメンテーション

の三種類のタスクがあります。犬・猫を二値分類するといった基本的なタスクと異なり、セグメンテーションタスクでは入力情報が画像であれば出力情報も画像の次元を持っているという、encoder-decoder タイプのモデルを使ってタスクを解くことが多いです。
その中でも、セグメンテーションといえば初手はこれ、という U-Net に関する論文を今更ながらパラッと読んでみたので感想をまとめてみます。

U-Net

2015年に提案されたエンコーダー・デコーダータイプのセグメンテーション用モデルで、今でも幅広くセグメンテーションタスクに使用されているモデルです。名前先行で個人的には分かりにくい（ようなそうでもないような）モデル図で論文中では紹介されている U-Net ですが、灰色の矢印ではなく本体（？）を追っていくと単純なエンコーダー・デコーダーのような形をしているのがわかります。

個人的な好みの図に修正して理解を進めてみます。基本構造は畳み込みとプーリングを使ったモデルであり、デコーダー部分ではエンコーダーからの出力を copy & paste する経路が追加されています^[1]。

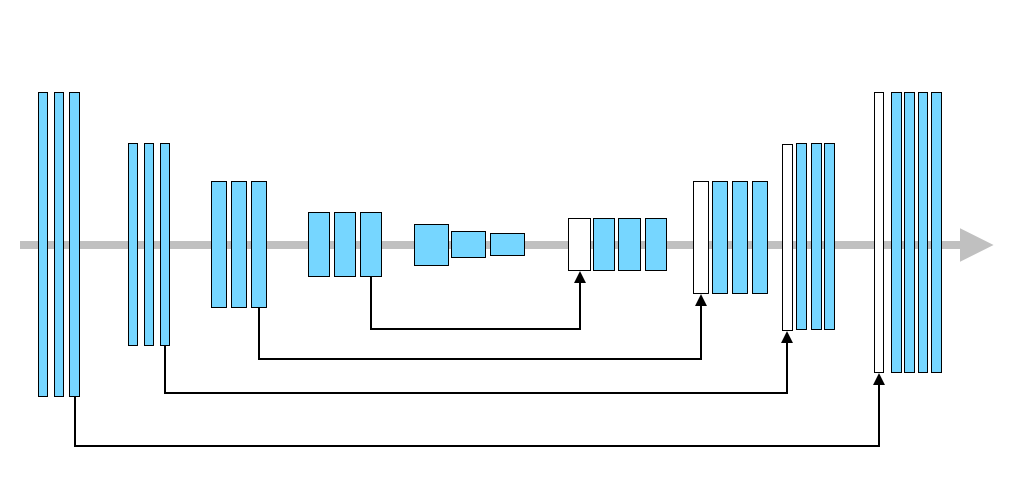
U-Net の全貌は以上で全てですが、以下で気になったことを少しピックアップしてみます。

up-convolution

デコーダー部分ではアップサンプリングを実装しており、deconvolution （論文では "up-convolution"）を使用しているようです。普通は deconvolution（逆畳み込み）というと transposed convolution のことを指し、

1. 入力特徴量マップを拡大する。このとき元の情報との隙間部分は padding していく（pytorch の ConvTransposed2d では padding のデフォルト値は 0）
2. 通常の畳み込み計算を実施

という手順を踏みます。

Loss function

セグメンテーションタスクについてよく使用される損失関数についてもざっと調べてみました。

Cross Entropy

分類タスクでよく使用されるクロスエントロピー（交差エントロピー）ですが、セグメンテーションタスクでも使用されます。クロスエントロピーの表式は

$$-\sum_{x}p(x)\log q(x)$$

でして、$p(x)$ が真の確率値、$q(x)$ が予測確率値になります。またここでの $x$ はデータの次元数を表しており、例えば 5　クラス分類のタスクであれば最終的に $[1, 0, 0, 0, 0]$ という真値と予測結果との比較になると思うのですが、このベクトルのインデックスを $x$ として表現しています^[2]。$p, q$ とも確率なので $[0, 1]$ の範囲の値をとり、そのため各 $x$ に対して $-p\log q$ は $[0, \infty]$ の範囲の値を取ります。$p$ と $q$ が似た値を取るとき（予測がうまくいっているとき）クロスエントロピーは小さくなります。

セグメンテーションタスクでも最終的な予測出力と真値とをピクセル単位で比較することで、クロスエントロピーを使用した学習を行うことができます。

Binary Cross Entorpy

Cross-Entropy の二値分類バージョンであり、

$$L = -y \log \hat{y} - (1-y) \log (1-\hat{y})$$

です。より簡単のために以下のような書き方もできます。 真値は $y=0, 1$ の二値であるのでそれらの場合に分けて書くと：

$$BCE = \left\{ \begin{array}{ll} -\log p& (y=1) \\ -\log(1-p)& (y=0) \end{array} \right.$$

となり、ここで

$$p_t = \left\{ \begin{array}{ll} p& (y=1) \\ 1-p& (y=0) \end{array} \right.:w$$

という $p_t$ を導入すると BCE は $L=-log p_t$ とすっきり書くことができます。

Focal Loss

Cross-Entropy をベースにした損失関数で、物体検知におけるクラス不均衡（class imbalance）に対応すべく 2017年に提案されたものです。例えば負例>>>正例のようなクラス不均衡があると BCE の場合であれば、損失値を計算したときに「とりあえず negative と予測しておけば loss が小さくなる」というような学習が進んでしまって、思うように精度が出ない問題に直面します。
そこで Focal Loss では BCE を修正した以下の表式を提案しています：

$$FL = -(1-p_t)^\gamma \log(p_t)$$

Dice Loss

画像間の類似度を計算するためによく使用されている Dice coefficient を用いた損失関数で以下の表式です：

$$L = 1 - \frac{1yp+1}{y+p+1}$$

所感

• 読んでみると案外中身のない（今だからかも、ですが）論文でした
• encoder-decoder に対して畳み込み前の情報を copy & paste して decoder に渡している、という内容が U-Net という名前のせいでややこしくなっている気もしました

出典

• U-Net: Convolutional Networks for Biomedical
  Image Segmentation
• A survey of loss functions for semantic
  segmentation
• Focal Loss for Dense Object Detection

脚注

1. このモデルの名前を U-Net にしようと言って周りもOKしたのは、何だか微笑ましいです。

2. $x$ と書かれるとベクトル感があって何だかわざわざややこしい定義だなぁとたまに思います。