はじめに
EM アルゴリズムについての勉強メモです。注釈にて自分の理解の限界を適宜補足していますので、これらを明確にできるように勉強を今後進めていければと思っています。
導入
以下では
p_\theta(x) = p(x; \theta) = p(x|\theta)
であるとします。論文によって表記方法は異なりますが、ここでは p_\theta(x) の表記で統一します。ただ、EMアルゴリズムを負う場合には p(x|\theta) のように陽に数式上に \theta が含まれていたほうが個人的には理解しやすい部分もあったりするので、適宜頭の中で補完していただければと思います。
精度の良い確率モデルを組むためには、観測値 x が従う未知の真の分布
を如何に推測するかにかかっているのですが、真の分布は直接はわかりません。実際には真の分布を近似した p_{\theta}(x)
を仮定して後段のタスクを解いていくことになります。学習(learning)とは
p_{\theta}(x) \approx p^\ast(x)
となるようなパラメータ \theta を探索することです。このようなモデル p(\cdot) やパラメーターセット \theta を発見することができれば、画像や自然言語を生成する高精度な AI を組むこともできるはずです。EM アルゴリズムは学習手法の一つです。
EMアルゴリズム
観測データ x が従う確率モデル p_\theta(x) のパラメータ \theta を求めたい場合には、通常であれば
\mathcal{L} = \ln p_\theta(x)
の尤度関数を最適化(最大化)するような \theta を探索する問題になります。しかしここでは、\partial p_\theta(x) / \partial \theta のように直接 \theta で微分するのが計算上困難である(intractableな)場合を想定します。
以上の場合に、潜在変数が従う分布 q(z) を新たに導入することで EM アルゴリズム(expectation maximization algorithm)と呼ばれる最適化手法を用いることができます。どのような q(z) に対しても尤度関数は以下のように展開することができ:
\ln p_\theta(x) = \mathcal{L}(q,\theta) + \mathrm{KL}(q||p)
ここで、\mathcal{L}(q,\theta) は q(z), \theta に対する汎関数で
\mathcal{L}(q,\theta) = \sum_z q(z) \ln \left\{ \frac{p_\theta(x,z)}{q(z)} \right\}
であり、\mathrm{KL}(q||p) はカルバックライブラー情報量
\mathrm{KL}(q||p) = - \sum_z q(z) \ln \left\{\frac{p_\theta(z|x)}{q(z)} \right\}
です。
カルバックライブラー情報量は \mathrm{KL}(q||p) \geq 0 を満たし、q(z) = p_\theta(z|x) の場合に等号が成立します。そのため展開された尤度関数に対して \mathrm{KL}(q||p) \geq 0 を用いると
\ln p_\theta(x) = \mathcal{L}(q,\theta) + \mathrm{KL}(q||p) \geq \mathcal{L}(q,\theta)
が成り立つことが分かります。そのため \mathcal{L} は尤度関数に対する下限であるという見方が可能となります。そのため \mathcal{L} を Evidence Lower Bound (ELBO) と呼んだりします。以上の関係性を図示すると次のようになります:

Figure 9.11, §9.4 The EM Algorithm in General, Bishop
最適化手順(Eステップ)
E ステップでは現在のパラメータ値(ex.初期値) を \theta^{\rm{old}} とし、この値を固定しつつ \mathcal{L}(q,\theta) を q(z) に対して最適化します。このとき尤度関数は
\ln p_{\theta^{\mathrm{old}}}(x) = \mathcal{L}(q,\theta^{\mathrm{old}}) + \mathrm{KL}(q||p)
と表され、\theta が固定されているので \ln p_\theta(x) の値は固定されています。そのため Figure 9.11 で見た関係性を思い出すと、全体の値 \ln p が固定された上で \mathcal{L} を最大化するには \mathrm{KL}(q||p)=0 となればいいことが分かります。 カルバックライブラー情報量の性質から
q(z) = p_{\theta^{\mathrm{old}}}(z|x)
の場合に \mathcal{L} が最大化されることが分かります。
最適化手順(Mステップ)
M ステップでは E ステップで求めた q(z) を固定して、\mathcal{L}(q,\theta) を \theta に対して最適化します。ここで \mathcal{L} が極大値を取っていなければ更に大きくなり、それに伴い対数尤度関数 \ln p の値も大きくなります(より最適値に近づいていきます)。\mathcal{L}(q, \theta) を最適化した際の \theta^{\mathrm{new}} に対してもはや
q(z) \neq p_{\theta^{\mathrm{new}}}(z|x)
となるため(q(z)は \theta^{\mathrm{old}} に対して求めたため、等号が成り立たなくなります)、カルバックライブラー情報量もゼロになりません。そのため下図のように、
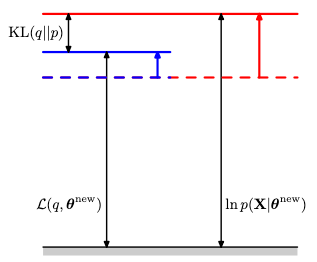
Figure 9.13, §9.4 The EM Algorithm in General, Bishop
\mathcal{L}も増加、\mathrm{KL}(q||p) も非負の値を持つようになり、対数尤度関数も \ln p_{\theta^{\mathrm{old}}}(x) \to \ln p_{\theta^{\mathrm{new}}}(x) のように新しい最適値(Eステップ時点より大きな値)に移動します。
まとめ
以上の EM アルゴリズムの流れは下図のようになり:

Figure 15.16, §15 Discrete latent variable, Bishop
iterative に最適化していく手法であることが分かります。
連続変数について
以上の EM アルゴリズムでは離散変数(総和を取る際に \sigma を使用していた)について議論を展開していたのですが、連続変数についても同様の議論を展開することができます。改めて対数尤度関数を \mathcal{L} と KL に分解する式展開を以下で追ってみます。
\begin{aligned}
\ln p_\theta(x) &= \ln \frac{p_\theta(x|z)p(z)}{p(z|x)} \\
\Leftrightarrow q(z|x)\ln p_\theta(x) &= q(z|x) \ln \frac{p_\theta(x|z)p(z)}{p(z|x)} \\
\Leftrightarrow \ln p_\theta(x) &= \int q(z|x) \ln \frac{p_\theta(x|z)p(z)}{p(z|x)} dz
\end{aligned}
ここで \int q(z|x) dz =1 を利用しました。続いて
\begin{aligned}
\ln p_\theta(x) &= \int q(z|x) \ln \left\{ \frac{p_\theta(x|z)p(z)}{p(z|x)} \frac{q(z|x)}{q(z|x)} \right\} dz \\
&= \int q(z|x) \left\{ \ln \frac{p_\theta(x|z)}{q(z|x)} - \ln \frac{p_\theta(z|x)}{q(z|x)} \right\} dz \\
&= \int q(z|x) \ln \frac{p_\theta(x|z)}{q(z|x)} - \int q(z|x) \ln \frac{p_\theta(z|x)}{q(z|x)} dz
\end{aligned}
より無事に展開できることが分かります。
参考文献
- Patten recognition and machine learning, Christopher M.Bishop
- Deep Learning - foundations and concept, Christopher M.Bishop



Discussion