ベイズ線形回帰モデル

はじめに

線形回帰モデルをベイズ的に取り扱うベイズ線形回帰についての記事です。"ベイズ的に取り扱う" ということや、実際どのような計算を行うことで予測できるのかなどをまとめています。

問題設定

まずはじめに、線形回帰モデルとベイズ線形回帰モデルについてまとめます。

線形回帰モデル

線形回帰モデル^[1]では

$$y(\rm{x}, \rm{w}) = \rm{w}^T\phi(\rm{x})$$

の形式を用いて、入力変数 $x$ に対する予測値 $y$ を計算します。$\phi(\rm{x})$ は基底関数と呼ばれ、非線形な基底関数を用いることもできます。ただしこの場合でもパラメータ $\rm{w}$ に対しては線形ですので^[2]線形モデルと呼ばれます。

ベイズ線形回帰モデル

ベイズ線形回帰モデルにとは、上述の線形回帰モデルをベイズ的に取り扱うモデルです。「ベイズ的な取り扱い」^[3]についての定義は書籍によってまちまちな印象ですが、

• 事前分布
• 尤度関数
• 周辺分布
• 条件づき分布

など、パラメータやデータに関して確率的取り扱いを行うことを指すことが一般的だと思います。決定論的な予測ではなく、確率的な予測を行うのがベイズ的な取り扱いだとして以下では説明を進めてみます。

事前分布

線形回帰モデルのパラメータ $\rm{w}$ の事前分布を導入します。ここでは簡単のために等方的ガウス分布である

$$p(\rm{w}) = \mathcal{N}(\rm{w}|0, \alpha^{-1}I)$$

を考えます。事後分布の性質も簡単に把握するために、ガウス分布などの共役な事前分布を選ぶことが多いです。また、事前にパラメータについての知見があればそれを踏まえた分布にすることも可能です。

事後分布

線形回帰モデルの目的は得られているデータセットからモデルパラメータを推定し、未知のデータへの予測を行うことです。そのため次に、対応するパラメータの事後分布を計算します。あるデータセット $D$（入力データ $X$ と目的変数 $Y$ の組）が観測されているとき、パラメータの事後確率はベイズの定理から

$$p({\rm{w}} | Y, X) = \frac{p(Y|X, {\rm{w}})p({\rm{w}})}{p(Y|X)}$$

です。

パラメータの推定について

パラメータの事後分布を計算することができましたので、$p({\rm{w}}|Y, X) = p({\rm{w}}|D)$ からサンプリング（確率変数を抽出する）することで、パラメータの値を推定することができます。パラメータ $\rm{w}$ が分かれば線形回帰モデル

$$y(\rm{x}, \rm{w}) = \rm{w}^T\phi(\rm{x})$$

の形も決まるので、未知のデータへの予測も可能になります。ただし $\rm{w}$ は確率変数としてサンプリングごとに値が変わるので、サンプリングした結果の平均などを用いるとより推論が安定すると言えます。以上のように、ベイズ線形回帰では事後分布を計算して、そこからサンプリングすることで確率的にパラメータ推定、未知のデータへの予測を行うことになります。

しかし一般的に、事後分布は解析的に評価することが困難です（数式としては表現できるが計算機での実行が難しいなど）。そこで使用されるテクニックがマルコフ連鎖モンテカルロ法（MCM法）と呼ばれる計算法であり、この計算法では任意の確率分布を定義することができます。そのため実際のベイズ的取り扱いでは必ずと言っていいほど、MCMC法がセットで登場します^[4]。

補足

ベイズ線形回帰モデルでは解析的に事後分布を計算することができます。そのためMCMC法は不要ではあるのですが、例として簡単であったためベイズ線形回帰モデルの事後分布を題材に以下のMCMC法について見ていきます。

マルコフ連鎖モンテカルロ法

ベイズ推論を用いた統計解析では事後分布

$$p({\rm{w}}| D)$$

を計算し、そこから値をサンプリングすることで予測などを行います。ただしニューラルネットワークなどを用いたモデルではこの事後分布 $p(\rm{w}| \rm{x})$ を解析的に求めることができないため、そこでマルコフ連鎖モンテカルロ法（Markov Chain Monte Carlo; MCMC法）と呼ばれるサンプリング手法を導入して問題の解決を行います。

ベイズ線形回帰モデルでは解析的に事後分布の形を求めることができたのですが、一般的にはベイズ推論の枠組みでの学習時には確率計算を何らかの形で近似的に求める方法が必要となります。大きく分けて、（１）サンプリングに基づく手法、と（２）最適化に基づく手法の２パターンがあります。サンプリング手法ではマルコフ連鎖モンテカルロ法などが有名で、最適化手法では変分推論が有名です。

問題設定

ベイズ線形回帰モデルを題材として、MCMC法を用いてパラメータ推定を行ってみます。まず観測データ $D$ として三角関数のデータにノイズを乗せた

$$y = \sin (2\pi x) + \epsilon$$

を考えます。

このデータを表現するためのモデルとして、基底関数にガウス基底関数を9個用いた^[5]

$$y({\rm{x}, \rm{w}}) = {\rm{w}^T\phi(\rm{x})} = \sum_{j=0}^8 w_j \exp \left\{ -\frac{(x-\mu_j)^2}{2s^2} \right\}$$

の形の線形モデルを考えます。ここでの目標はデータの情報 $D$ から真のパラメータ値 ${\rm{w}} = \left\{ w_0, w_1, w_2, w_3, w_4, w_5, w_6, w_7, w_8 \right\}$ を復元することです。

各種手法

マルコフ連鎖モンテカルロ法と一口に言っても実際の計算方法・実装方法は様々な手法があり、ここでは代表的な（簡単に実装できた）メトロポリスヘイスティングス法を紹介します。

メトロポリス・ヘイスティングス法

サンプリングを行いたい確率分布を目標分布 $p(z)$ と呼びます^[6]。$p(z)$ からは直接サンプリングできないため、提案分布 $q(z)$ と呼ばれる分布を準備し以下の手順に従って提案分布からサンプリングすることで、結果的に目標分布からサンプリングした結果に近似できるという手法です。

1. 初期値 $z_0$ を決める
2. 提案分布 $q(z)$ から、次の候補 $z_\star$ をサンプリングする
3. 採択確率を計算する

$$r = \frac{p(z_\star)q(z_t|z_\star)}{p(z_t)q(z_\star|z_t)}$$

4. 確率 $\min(1, r)$ でサンプリング候補を採用し（$z_{t+1} \leftarrow z_\star$）、そうでない場合は $z_{t+1} \leftarrow z_t$ とする

手順(2)~(4) を繰り返して得られたサンプリング結果 $z_0, z_1, ..., z_T$ は目標分布 $p(z)$ からサンプリングした結果に近似できるというのが、メトロポリスヘイスティングス法です。

メトロポリスヘイスティングス法では採択確率の計算時に目標分布の比 $p(z_\star)/p(z_t)$ を取っているので、事後分布で解析的に計算できない分母の部分（$p(D)$）が相殺され、そのため計算が可能となっています。

実装

提案分布にガウス分布を用いて^[7]、メトロポリスヘイスティングス法を用いてベイズ線形回帰モデルのパラメータ推定を行ってみます。まず目標分布を以下のように実装します：

def gauss(idx, x, D=9):
    """
    ガウス基底関数
    """
    mu = idx * (1 / (D - 1))  # 基底関数の中心を等間隔に配置
    sigma = 0.1  # 全基底関数で一定
    return np.exp(-0.5 * ((x - mu) ** 2) / sigma ** 2)

def target(w):
    """
    目標分布
    """
    D = 9

    def prior(w):
        """
        パラメータの事前分布
        """
        mu = np.zeros(D)
        sigma = np.eye(D)
        coeff = 1 / (2 * np.pi * np.sqrt(np.linalg.det(sigma)))
        exponent = np.exp(-0.5 * (w - mu).T @ np.linalg.inv(sigma) @ (w - mu))
        return coeff * exponent
    
    def likelihood(x_data, y_data, w):
        """
        尤度関数, p(D|w)
        """
        def p(x_i, y_i, w):
            mu = sum(w[j] * gauss(j, x_i) for j in range(D))
            sigma = 1.0  # 観測ノイズの標準偏差
            coeff = 1 / (np.sqrt(2 * np.pi) * sigma)
            exponent = np.exp(-0.5 * ((y_i - mu) / sigma) ** 2)
            return coeff * exponent
        
        return np.prod([p(x_i, y_i, w) for x_i, y_i in zip(x_data, y_data)])
    
    return likelihood(x_data, y_data, w) * prior(w)

実際のメトロポリスヘイスティングス法に従ったサンプリング部分を以下のように実装します：

def metropolis_hastings(target, initial_sample, iterations):
    samples = [initial_sample]
    accept_count = 0
    for i in range(iterations):
        current_sample = samples[-1]
        proposal_sample = np.random.randn(D)
        accept_prob = min(1, target(proposal_sample) / target(current_sample))
        if np.random.rand() < accept_prob:
            samples.append(proposal_sample)
            accept_count += 1
        else:
            samples.append(current_sample)
    # print(f"Acceptance rate: {accept_count / iterations}")
    return np.array(samples)

以下のように 10,000回のサンプリングを行ってみます。

D = 9
initial_sample = np.zeros(D) 
iterations = 10000
samples = metropolis_hastings(target, initial_sample, iterations)

サンプリングした結果の samples は、(10001, 9) 次元のベクトルで、10001 個の線形モデルの作成・予測値の計算を行います。それらを用いることで推論結果の平均・分散を計算することができます。以下に、サンプリング結果の平均値で作成した線形モデルを実線、分散をハッチで表現してみます：

# 新しい x 値の範囲を定義
x_new = np.linspace(0, 1, 100)

# サンプリングされたパラメータを使用して y の予測値を計算
y_pred_samples = np.array([sum(w[j] * gauss(j, x_new) for j in range(D)) for w in samples])

# 予測値の平均と標準偏差を計算
y_pred_mean = np.mean(y_pred_samples, axis=0)
y_pred_std = np.std(y_pred_samples, axis=0)

# 予測分布のプロット
fig, ax = plt.subplots(figsize=(8, 5))
ax.scatter(x_data, y_data, marker="o", label='Original data', facecolor="None", edgecolor="black")
ax.plot(x_new, y_pred_mean, 'r-', label='Predicted mean')
ax.fill_between(x_new, y_pred_mean - 2*y_pred_std, y_pred_mean + 2*y_pred_std, color='red', alpha=0.2, label='Predicted std deviation')
ax.legend()
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_xlim(0, 1)
ax.set_title('Bayesian Linear Model Predictions')
plt.show()

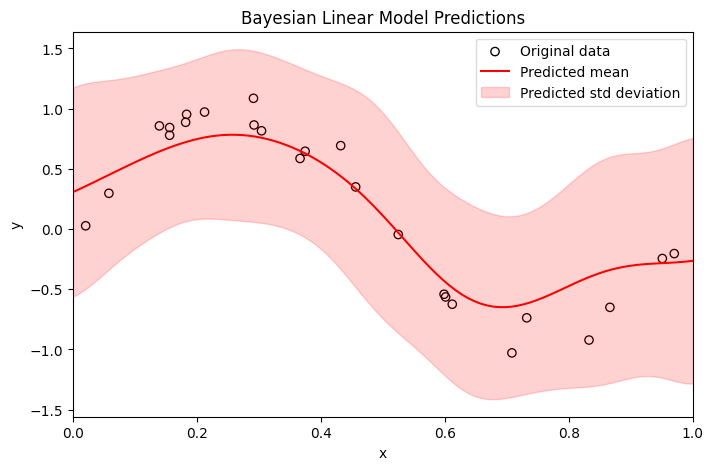
適当に実装してみたのですが、それっぽくはなっているので満足しました。雰囲気は掴めたかと思います。

その他

その他にサンプリング手法はたくさん実装されており、

• ハミルトニアンモンテカルロ法
• ギブスサンプリング

などがありました^[8] 。これらの手法の違いなども、これから時間を見つけて勉強していければと思っています。

最後に

マルコフ連鎖モンテカルロ法では無限に計算を続けることができれば真の分布から得られたものと同一視できるという利点があるのですが、必要なサンプルサイズの増大によって計算コストが増大してしまうという欠点があります。そこで最近では最適化に基づく事後分布の近似手法があり、その中で変分推論法などが出てきます。変分推論なども勉強できればと思っています。

脚注

1. 入力変数 $x$ に対して線形ではなく、パラメータ $w$ に対して線形であるモデルです。ただし $y=w_0 + w_1x_1+...$ のモデルも単に線形回帰と呼びます（Bishop, p.136）

2. $\rm{w}$ の二次以上の項は無いです。

3. Bishopでは「事前分布を導入するところから、線形回帰モデルのベイズ的な取り扱いについて説明する.」との導入がありますが、確率分布を導入する部分がベイズ的な取り扱いの肝です。

4. ベイズ的な取り扱い = MCMC法ではなく、事後分布から直接サンプリングできないのでMCMC法を使用する、というような流れは頭に入れておきましょう。

5. Bishop p.155 の設定をそのまま拝借しているだけで、「ガウス基底関数を9個」用いることに特別な意味はないです。ただ個数が具体的な方がイメージが付きやすいかと思います。

6. ここでの例はパラメータの事後確率分布 $p(\rm{w}| \rm{Y}, \rm{X})$

7. よく例としてガウス分布が使われますが、問題によって一様分布を用いる場合やその他の分布を用いる場合などがあります。

8. 「ベイズ深層学習」p.86