"回帰"とは何か？ Why is the term "regression" used?

The English translation follows the Japanese text.

統計学や機械学習に関わる人たちが普段何気なく使っている"回帰"という言葉について考えてみる。回帰という言葉を辞書で調べてみると以下のようになっている。

［名］(スル)ひとまわりして、もとの所に帰ること。「伝統への―」

一方で統計学や機械学習の分野の人達が"回帰"と言ったときには以下のような意味で使っている。

結果となる数値と要因となる数値の関係を調べて、それぞれの関係を明らかにする統計的手法。

これらの用法の繋がりは全く自明ではない。ここではなぜ統計学や機械学習の分野で"回帰"という言葉が使われるようになったかについて考えてみたい。

まず、図1のようなデータが与えられたとする。このとき、このデータに2変量正規分布と回帰直線を当てはめることを考える。

図1
当てはめた結果、図2が得られた。ただし、2変量正規分布は最尤推定法によって当てはめ、回帰直線は最小二乗法によって当てはめた。

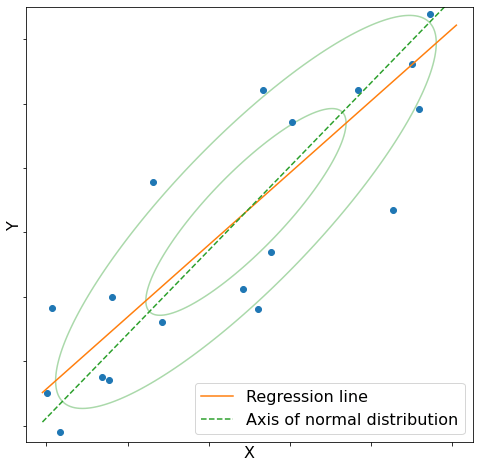
図2
この図から以下のことが分かる。

1. 回帰直線と正規分布の軸は異なる。
2. 正規分布の軸に比べ、回帰直線の傾きは緩やかである。
3. (図には示していないが1.と2.から $y$ の $x$ に関する回帰と $x$ の $y$ に関する回帰の結果が異なることも分かる。)

実際には回帰直線は2変量正規分布の条件付き期待値 ${\rm E}[y|x]$ と一致している。さらに2変量正規分布の軸の傾きを $a$ 、$x$ と $y$ の相関係数を $\rho \ (>0)$ とすると、回帰直線の傾きは $\rho a$ となる。(相関係数が負の場合には若干数式の変更が必要。) また、回帰直線と2変量正規分布の軸は点 $({\rm E}[x], {\rm E}[y])$ で交わる。

ここで $x$ を父親の身長、 $y$ を息子の身長としよう。そしてそれらが2変量正規分布に従うとし、さらに世代間の定常性を仮定する。すなわち ${\rm E}[x]={\rm E}[y]$ 及び ${\rm Var}[x]={\rm Var}[y]$ を仮定する。このとき2変量正規分布の軸の傾きは1となる。すると先の図2で見たように以下の関係が成り立つ。

$${\rm E}[y|x] < x \quad {\rm if} \ x > E[x],$$

$${\rm E}[y|x] > x \quad {\rm if} \ x < E[x]$$

すなわち、父親の身長が平均よりも大きいとき息子の身長は父親の身長よりも小さくなる傾向があり、逆に父親の身長が平均よりも小さいとき息子の身長は父親の身長よりも大きくなる傾向がある。すなわち第2世代は平均の方向に"回帰"するのである。これが統計学における"回帰"の謂れである。

参考文献: 統計ライブラリー 回帰分析 (佐和 隆光)

Let's consider the word "regression", which is usually used casually by people involved in statistics and machine learning. A dictionary search of the word "regression" reveals the following.

the act of going back to a previous place or state; return or reversion.

On the other hand, when people in the fields of statistics and machine learning use the term "regression", they mean the following.

the analysis or measure of the association between one variable (the dependent variable) and one or more other variables (the independent variables)

The connection between these usages is not at all obvious. Here we will consider why the term "regression" came into use in the fields of statistics and machine learning.

First, suppose that the data shown in Figure 1 are given. We then consider fitting a bivariate normal distribution and a regression line to this data.

Figure 1
As a result of the fitting, Figure 2 was obtained. Note that the bivariate normal distribution was fitted by the maximum likelihood estimation method and the regression line was fitted by the least squares method.

Figure 2
From this figure it can be seen that.

1. the axis of the normal distribution and the regression line are different.
2. the slope of the regression line is slower than the axis of the normal distribution.
3. (Although not shown in the figure, from 1. and 2. we can also see that the results of the regression of $y$ on $x$ and the regression of $x$ on $y$ are different.)

Actually, the regression line corresponds to the conditional expectation of the bivariate normal distribution ${\rm E}[y|x]$. Furthermore, if the slope of the axis of the bivariate normal distribution is $a$ and the correlation coefficient between $x$ and $y$ is $\rho \ (>0)$, the slope of the regression line is $\rho a$. (If the correlation coefficient is negative, the formula needs to be slightly modified.) Also, the axis of the bivariate normal distribution and the regression line intersect at the point $({\rm E}[x], {\rm E}[y])$.

Let $x$ be the height of the father and $y$ the height of the son. Assume that they follow a bivariate normal distribution and further assume stationarity between generations. In other words, assume that ${\rm E}[x]={\rm E}[y]$ and ${\rm Var}[x]={\rm Var}[y]$. In this case, the slope of the axis of the bivariate normal distribution is 1. Then, as seen in Figure 2 above, the following relationship holds.

$${\rm E}[y|x] < x \quad {\rm if} \ x > E[x],$$

$${\rm E}[y|x] > x \quad {\rm if} \ x < E[x]$$

That is, when the father's height is greater than the average, the son's height tends to be smaller than the father's height, and conversely, when the father's height is smaller than the average, the son's height tends to be greater than the father's height. In other words, the second generation "regresses" in the direction of the mean. This is the origin of "regression" in statistics.

References: 統計ライブラリー 回帰分析 (佐和 隆光)