einopsを理解する

はじめに

この記事はほぼ横浜の民 Advent Calendar 2023の12日目の記事です。

tensorの操作は毎度雰囲気で実装しているので、この機会にeinopsに入門してみます。 　
同じことをするための実現手段がnumpyとpytorchで違うため都度ググっているのを辞めたい、というのが大きなモチベーションです。

直感的な記述ではありますが、意図とは違う記述をしてしまいそうな部分もあるので、丁寧に入門していきます。
そのため公式チュートリアル1のrearrangeメソッドに関する部分が題材となります。

einopsとは

リンク

公式ページとgithubは以下です。

https://einops.rocks/

https://github.com/arogozhnikov/einops

特徴

主な特徴は以下です。

• 直感的な記述でtensorを操作できる
• numpyに限らずpytorch, tensorflow, jaxなど様々なライブラリで保持しているtensorでも同じ記述で操作できる
• 記述の中で各軸の内容を記載できるので、コメントが無くても可読性の高いコードになりやすい

githubのREADME冒頭にある動画が出来ることのイメージが湧きやすいので、そちらも参照してください。

また、einopsの名前は、Einstein-Inspired Notation for operations の略で、アインシュタインの縮約記法を参考に実現されているようです。　　
※ アインシュタインの縮約記法が気になる方はこちらを参考にしてください。

einops入門

前提

Python 3.10, einops==0.7.0 で動作確認しています。
また公式チュートリアル1をベースとしています。

入門

扱うデータ

(6, 96, 96, 3) のnumpy tensorデータimsを扱います。
ims[0], ims[1]などで(96, 96, 3)のカラー画像にアクセスできます。

基本の操作1 軸の入れ替え

numpyのtensor

例えば画像を反転するような操作は、einopsでは以下のように記載できます。
h, w, c などを使って記載することで実装の中で各軸の内容を明記することができるので可読性が高くなりやすいようです。

from einpos import rearrange, reduce, repeat
ims0_rot90 = rearrange(ims[0], 'h w c -> w h c')

ims[0]	ims0_rot90

これをnumpyで記載すると以下のようになります。
軸の順番を指定することで実現していますが、各軸が何を意味するかは自明ではなく、適宜コメント等で補足する必要があります。

ims[0].transpose(1, 0, 2)

pytorchのtensor

pytorchのtensorの場合でも、einopsを使えばnumpyのtensorの場合と同様の記載で操作できます。

ims0_torch = torch.tensor(ims[0])
rearrange(ims0_torch, 'h w c -> w h c')

一方、pytorchで記載してみると以下のようになります。
numpyではtransposeメソッドでしたが、pytorchではpermuteメソッドです。

ims0_torch = torch.tensor(ims[0])
torch.permute(ims0_torch, (1, 0, 2))

基本の操作2 tensorの合成

imsを構成する6種類のカラー画像を高さ方向に結合する操作を以下のように記載できます。

ims_composed_h = rearrange(ims, 'b h w c -> (b h) w c')
ims_composed_w = rearrange(ims, 'b h w c -> h (b w) c')

ims_composed_h	ims_composed_w

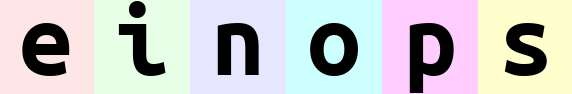これをnumpyで記載すると以下のようになります。(concatenateメソッド)

ims_composed_h = np.concatenate([im for im in ims], 0)
ims_composed_w = np.concatenate([im for im in ims], 1)

またpytorchで記載すると以下のようになります。(catメソッド)

ims_torch = torch.tensor(ims)
ims_composed_h = torch.cat([im for im in ims_torch], 0)
ims_composed_w = torch.cat([im for im in ims_torch], 1)

理解の確認として、以下のように記載した場合どうなるか分かりますか。

ims_composed_w = rearrange(ims, 'b h w c -> h (w b) c')

答え

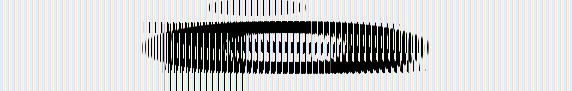
感覚的な理解としては、
(b w)の順序で記載したときが bコ（ここでは6コ）、サイズwのtensorが並ぶのに対し、
(w b)の順序で記載するとwコ、サイズbのtensorが並ぶことになります。

基本の操作3 tensorの分解

tensorの合成における次元の変化

分解に入るまえに、さきほどの合成したときに各次元の大きさがどのように変化しているかみておきます。
比較的分かりやすいかと思いますが、合成された次元の大きさは元の大きさを乗算した結果になっています。(6*96 = 576)

print(ims.shape) # (6, 96, 96, 3)
print(rearrange(ims, 'b h w c -> h (b w) c').shape)  # (96, 576, 3)

tensorの分解

合成の逆の操作だと考えれば各次元の大きさがどのようになるかは明らかだと思います。

print(rearrange(ims, '(b1 b2) h w c -> b1 b2 h w c', b1=2).shape) # (2, 3, 96, 96, 3)

合成と分解の組み合わせ

その1

縦2横3に並べる操作は、以下のように記載できます。

rearrange(ims, '(b1 b2) h w c -> (b1 h) (b2 w) c', b1=2)

以下のように記載した場合どうなるでしょうか。

rearrange(ims, '(b1 b2) h w c -> (b2 h) (b1 w) c', b1=3)

答え

感覚的な理解としては、
(b1 b2), b1=3 とした場合、3コ、サイズ2のtensorが並ぶ形になるので、各要素を"einops"とすると、"ei", "no", "ps"のようにグループ分けされます。
これを(b2 h) (b1 w)で並べるので、高さ方向は2コ、サイズhのtensorが並んでいて、それらはそれぞれ"ei", "no", "ps"からなります。

また、以下のように記載した場合どうなるでしょうか。

rearrange(ims, '(b1 b2) h w c -> (h b2) (b1 w) c', b1=3)

答え

感覚的な理解としては、
(b1 b2), b1=3 とした場合、3コ、サイズ2のtensorが並ぶ形になるので、各要素を"einops"とすると、"ei", "no", "ps"のようにグループ分けされます。
これを(h b2) (b1 w)で並べるので、高さ方向はhコ、サイズ2のtensorが並んでいて、それらはそれぞれ"ei", "no", "ps"からなります。

その2

各画像の幅を半分に高さを2倍にする操作は以下のように記載します。
このとき、あくまでもrearrangeなので使われている各ピクセルは元のimsの要素であり、順番が入れ替わっただけなことに注意が必要です。

rearrange(ims, 'b h (w w2) c -> (h w2) (b w) c', w2=2)

最後に、以下のように記載した場合どうなるでしょうか。

rearrange(ims, 'b h (w w2) c -> (w2 h) (b w) c', w2=2)

答え

感覚的な理解としては、
00, 01, 02, 03, …
10, 11, 12, 13, …
を(w w2), w2=2 によって
00-01, 02-03, …
10-11, 12-13, …
にグループ分けします。(wコ、サイズ2のtensorが並ぶイメージです）
これを、(h w2)で高さ方向に並べる場合は、hコ、サイズ2のtensorが並ぶことになるので、
00, 02, …
01, 03, …
10, 12, …
11, 13, …
となり拡大したような画像になります。
一方で、(w2 h)で高さ方向に並べると、2コ、サイズwのtensorが並ぶことになるので、
00, 02, …
10, 12, …
…
01, 03, …
11, 13, …
のようになるため、上下に複製したかのような結果になります。

まとめ

ここまで読んでいただきありがとうございます。
チュートリアル1の途中までではあるものの、einopsを使うメリットを体感できた気がしています。

すべてを明記はしていませんが、今回扱ったrearrangeメソッドでnumpyのtransopose, reshape, stack, concatenate, squeeze/unsqueeze, expand_dimsに相当する処理が扱えます。

rearrange以外にも基本的なメソッドとしてreduce, repeatもあるので、チュートリアルの続きで勉強しようと思います。そちらも別記事にするかもしれません。