ヒストグラム内の最大長方形を求めるアルゴリズム

ヒストグラム内の最大長方形を求めるアルゴリズム
プログラム内では、ヒストグラムを整数のリストで表します。

[8, 10, 4, 6, 8, 6, 2, 2]

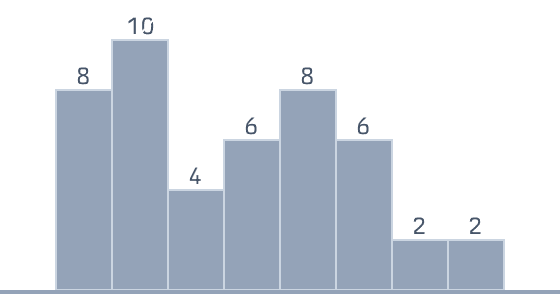
素直な求め方

それぞれのビンにおいて、そのビン高さを基準に左右に高さを調べていきます。
基準以上の高さを持つビンが左右に何個あるかで横幅を導き、面積を求めます。

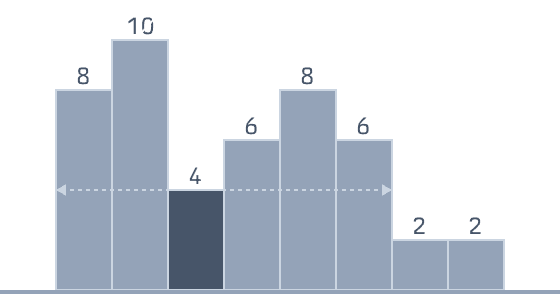
def largestRectangleArea(hist):
    max_area = 0
    for index, height in enumerate(hist):
        left, right = index, index
        # 左側の境界を見つける
        while left > 0 and hist[left - 1] >= height:
            left -= 1
        # 右側の境界を見つける
        while right < len(hist) - 1 and hist[right + 1] >= height:
            right += 1

        width = right - left + 1
        max_area = max(max_area, width * height)

    return max_area

効率的な求め方

いずれかのビンの高さが、最大の長方形の高さと一致します。
同様に、いずれかのビンの辺が、最大の長方形の辺と一致します。

ビンを順番に見ていくとします。
今見ているビンの左辺の位置を基準に、左側にどれだけ領域を伸ばして長方形を作れるかを考えます。

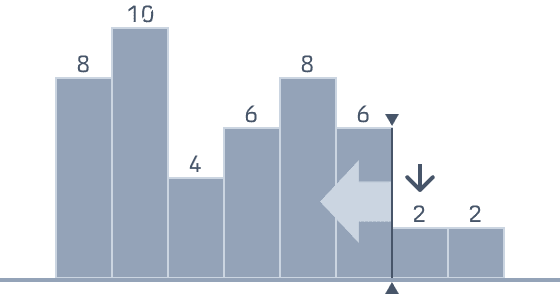
左側にいくら伸ばせるかは、低いビンの位置によって決まります。
今基準としている位置の高さより、低いビンの右辺の位置まで伸ばすことができます。

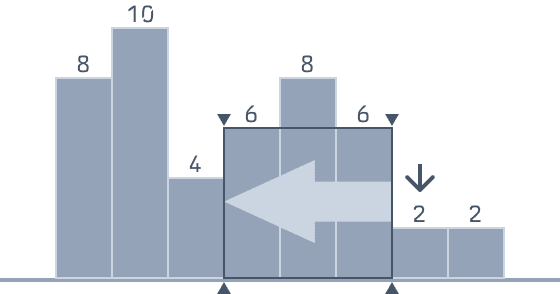
ここで、左側にあるすべてのビンの高さを調べると「素直な求め方」と変わりないので、動的計画法を用います。

動的計画法を用いる

動的計画法とは、計算済みの結果を保存しておき、再利用することで計算量を削減する手法です。

最初にビンを順番に見ていく際、左側にどれだけ伸ばせるかが分かる情報を保存しておきます。
左側にいくら伸ばせるかを知るには、低いビンの位置が必要です。
そのため、次のアルゴリズムに従ってビンの位置をスタックに保存しながら、最大の長方形を求めます。

アルゴリズム

1. ヒストグラムを左から順番に見ていく
2. 今見ているビンが、スタックの最後のビンよりも高い、もしくはスタックが空の場合
   • スタックにビンを追加
3. 今見ているビンが、スタックの最後のビンよりも低い場合
   • スタックの最後のビンを取り出す
     • 取り出したビンを高さを、長方形の高さとする
       • スタックに残っている最後のビンの右辺が、長方形の左辺
       • 見ているビンの左辺の位置が、長方形の右辺
     • 面積を計算して、大きければ最大面積を更新する
   • スタックの最後のビンが今のビンよりも低くなるまで繰り返す

上記のアルゴリズムに従うことで、スタックの中身はこのようになります。

• 昇順になっている
• ヒストグラム左側にあるビンから順番にスタックされている
• 取り出す際は、ヒストグラムの右側にあるビンから順番に取り出される

昇順にスタックされていることがキーです。

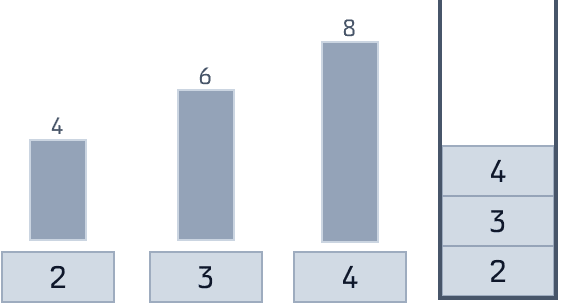
いづれかのスタックされているビンに注目したとき、その前にスタックされたビンの方が必ず低くなります。
そのため、注目しているビンから左側にいくら伸ばせるかは、その前にスタックされているビンの位置で求めることができます。

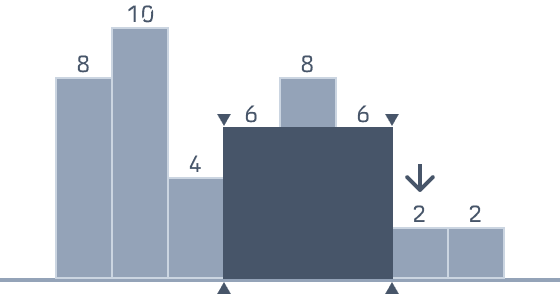
長方形の大きさを求めるタイミングは、スタックの最後のビンより低いビンが来たときです。
低いビンの左辺の位置が、長方形の右辺の位置となります。

それでは以下がPythonでの実装になります。

def largestRectangleArea(hist):
    target = [0] + hist + [0]
    stack = []
    max_area = 0

    for i, height in enumerate(target):
        while stack and target[stack[-1]] > height:
            h = target[stack.pop()]
            w = i - stack[-1] - 1
            max_area = max(max_area, h * w)
        stack.append(i)

    return max_area

気づいている方もいると思いますが、説明したアルゴリズムに素直にヒストグラムを渡すと、両端を計算してくれません。
そのため、両端に高さ0のダミーのビンを追加しています。

これで、ヒストグラム内の最大長方形を求めることができます。