Linuxのメモリ割り当てアルゴリズム Buddy Memory Allocation編

はじめに

世界中で広く使われているLinuxがどのようなメモリ割り当てアルゴリズムを使って物理メモリを管理しているのか、その仕組みには以前から興味がありました。
そこで、Linuxでメモリ割り当てアルゴリズムとして使用されている、Buddy Memory AllocationとSlab Allocationを自作しているOSに実装したのですが、日本語の記事や情報があまりなく実装するのに結構時間がかかってしまいました。（両者とも日本語版Wikipediaにすら載っていませんでした）なので、日本語の情報が少ないのならばこの機会に残しておこうと思い、この記事を書くことにしました。
本記事では、Buddy Memory Allocationに焦点を当て、その仕組みを紹介していきたいと思います。

前提

メモリ管理とは

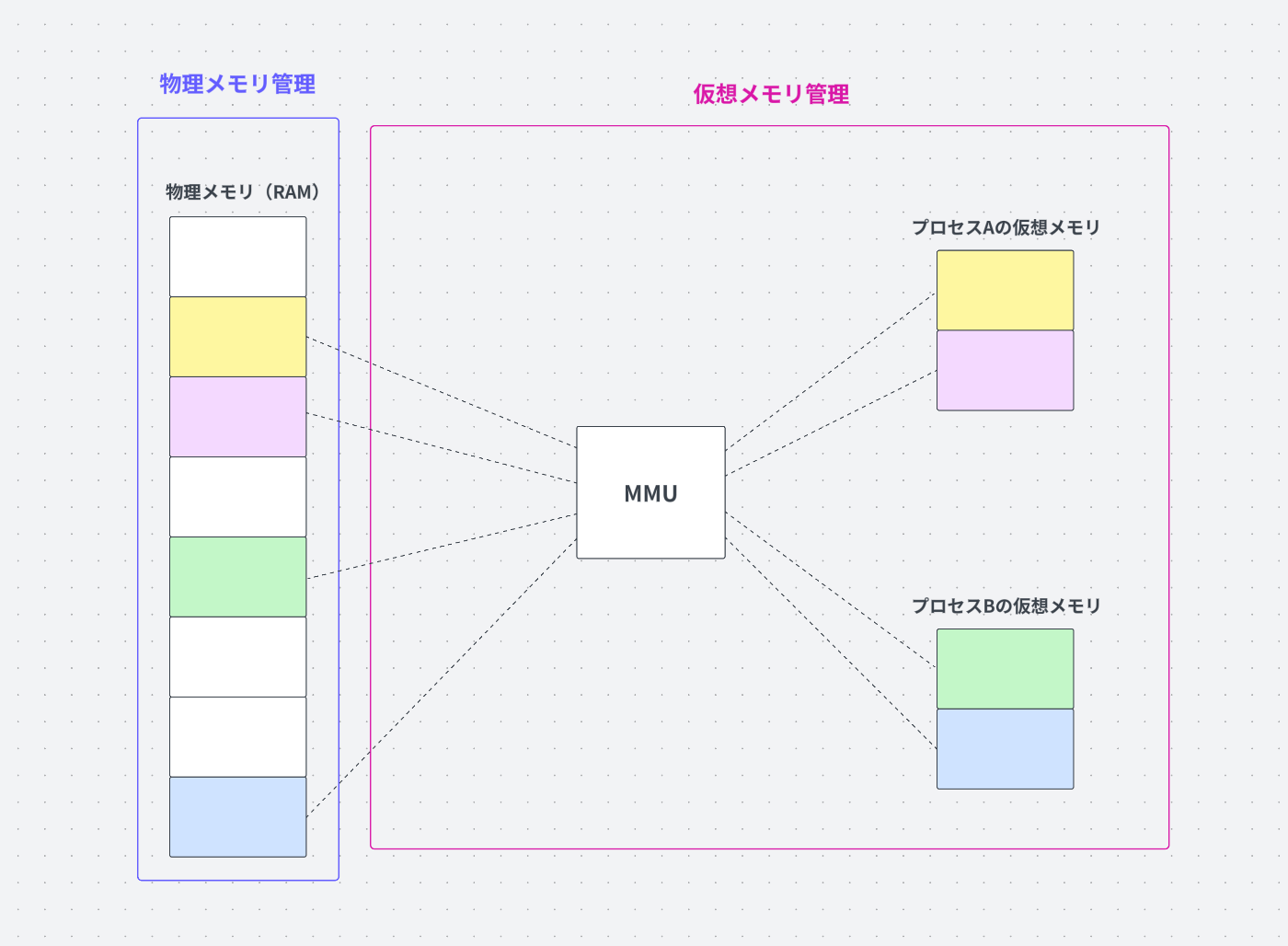
物理メモリ管理と仮想メモリ管理
OSのメモリ管理には、主に「物理メモリ管理」と「仮想メモリ管理」の二つの種類が存在します。
物理メモリ管理は、PCに搭載されているRAM（メインメモリ）の管理を意味し、必要な時に必要な量のメモリがプロセスに割り当てられるようにメモリを確保、解放することを指します。

仮想メモリ管理は、物理メモリの容量を超えるメモリ要求に対応し、各プロセスに独立したメモリ空間を提供することを目的としています。
主題から逸れるので詳しく紹介はしませんが、この仕組みによって、各プロセスに独立した仮想アドレス空間が提供され、プログラムは物理メモリの実際の配置を意識せずに済みます。

今回紹介するアルゴリズムは物理メモリを管理するためのものです。

Linuxのメモリ割り当てアルゴリズムの簡略図

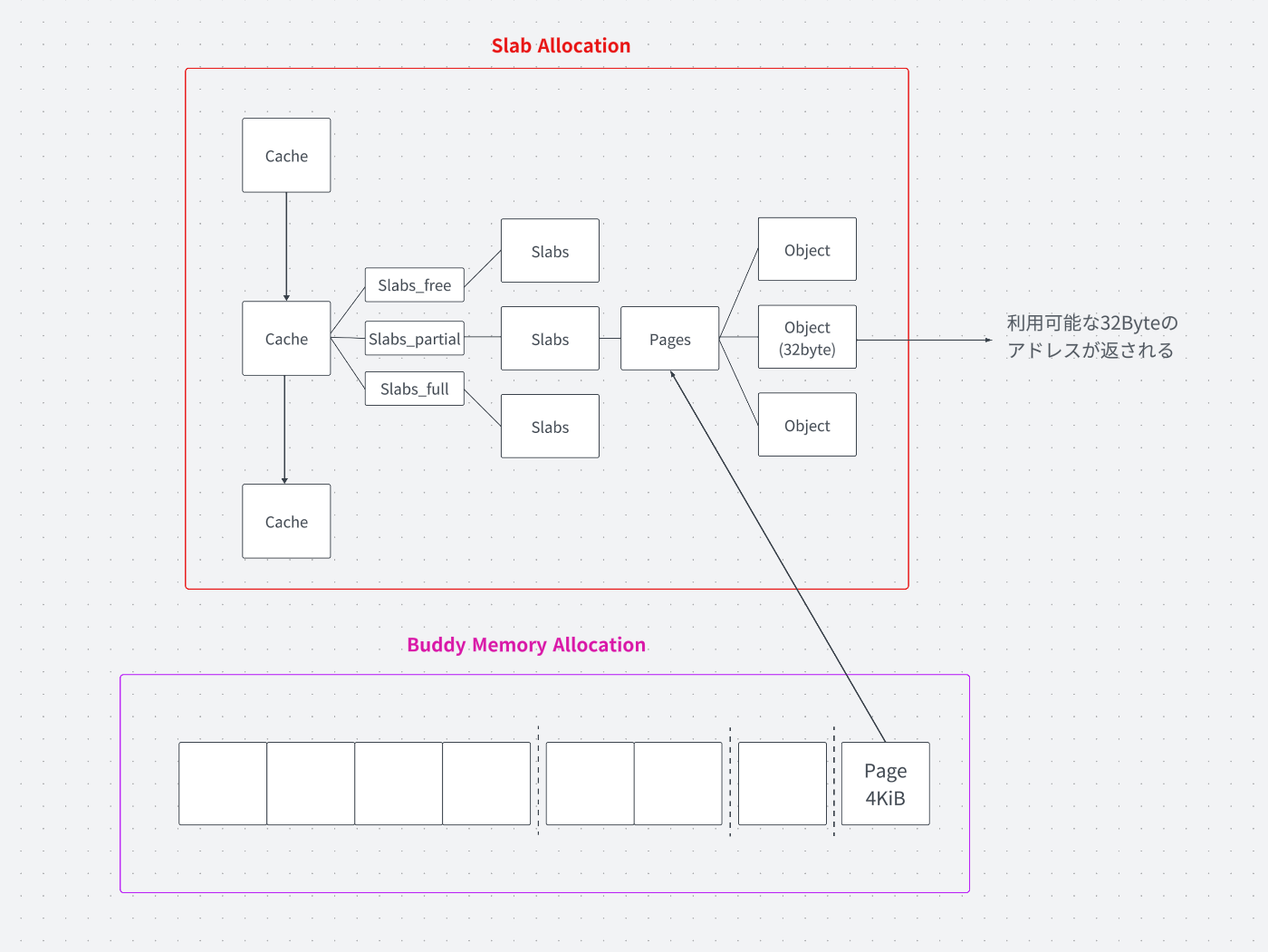
32byteのメモリを割り当てる様子
Linuxでは、メモリ割り当てにBuddy Memory AllocationとSlab Allocationの２つの主要なアルゴリズムが使用されています。これらのアルゴリズムは異なる役割を担っていますが、組み合わせることによって効率的なメモリ管理を実現しています。

このシリーズでは、２つの記事を通して上図の全体像を理解することを目指します。

本記事では、Zoneなどの概念は割愛し、主に割り当てアルゴリズムに焦点を当てています。

Buddy Memory Allocation

歴史

Buddy Memory Allocationは、1963年にHarry Markowitz氏によって考案されたアルゴリズムです。執筆時点では2023年なので、60年前に発見されたアルゴリズムとなります。60年前となると初めて東京オリンピックが開催された頃なので、歴史のあるアルゴリズムだなと思います。（大体のアルゴリズムは歴史がありますが...）

そんな60年前に考案されたアルゴリズムが、現在もLinuxのメモリ割り当てアルゴリズムとして利用されています。特に技術トレンドの移り変わりが早いソフトウェア業界ですが、アルゴリズムのような基本的な概念は、急激に変化することは少なく、変わったとしてもその知識は陳腐化することなく他の分野やアルゴリズムに応用できることが多いので、めんどくさがりの自分にとっては、性に合う分野だなと感じています。

概要

Buddy Memory Allocationは、外部フラグメンテーションを最小限に抑えるために考え出されたメモリ割り当てアルゴリズムです。
外部フラグメンテーションとは、メモリの空き容量は十分あるのにも関わらず、連続している空き領域が少なく、小さな空き領域が点在してしまっているためにメモリを割り当てられない状況のことを指します。

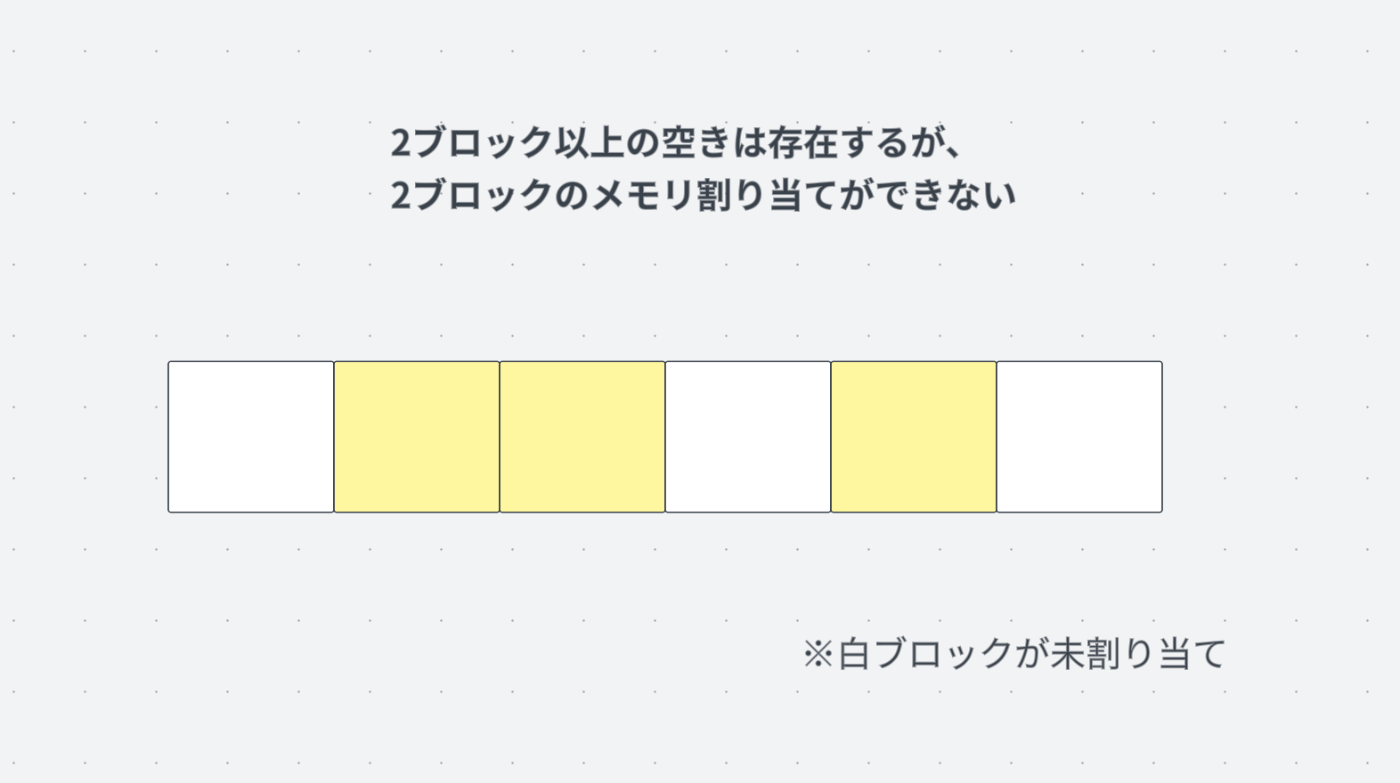
外部フラグメンテーションの発生の様子

これは、3ブロックの空きがあるのにも関わらず、２ブロックの割り当てが行えない様子を示しています。メモリ割り当ては、連続したメモリ領域を確保する必要があるので、2ブロックの連続した空きがない上図では割り当てが行えないのです。この状況こそが外部フラグメンテーションです。

このアルゴリズムではメモリの割り当てと解放をメモリブロックという単位で行います。
メモリブロックは2の冪乗のサイズである必要があり、Linuxでは4KiB(2^12バイト)と定義されています。4KiBというサイズは、Linuxのページング機構で使われる最小のページサイズに相当し、これによって物理メモリと仮想メモリの間でのマッピングを効率的に行うことができます。

外部フラグメンテーションの発生を最小限に抑えるために、どのようにメモリブロックの割り当てと解放を行うかを紹介していきます。

なお、本記事において1メモリブロックのサイズは4KiBとします。

メモリの割り当て

メモリの割り当て要求が発生すると、要求されたサイズを超える最小の2の冪乗数のブロックが割り当てられます。

10KiBのメモリ要求をしている様子

例えば、10KiBのサイズのメモリ要求があった場合、16KiB（2^2 * 4KiB）のブロックが割り当てられます。一見、12KiB(ブロックが3個)で十分かのように思えますが、要求されたサイズを超える最小の2の冪乗数を満たしている16KiBが選ばれます。なお、この時の指数(2^nのn)をorderと呼び、この例では、order-2のブロックが割り当てられたことになります。
2の冪乗数のブロックを割り当てる理由については、次章で詳しく説明します。

次にメモリが要求が発生した際に、内部でどのようにブロックを確保するかを見ていきます。

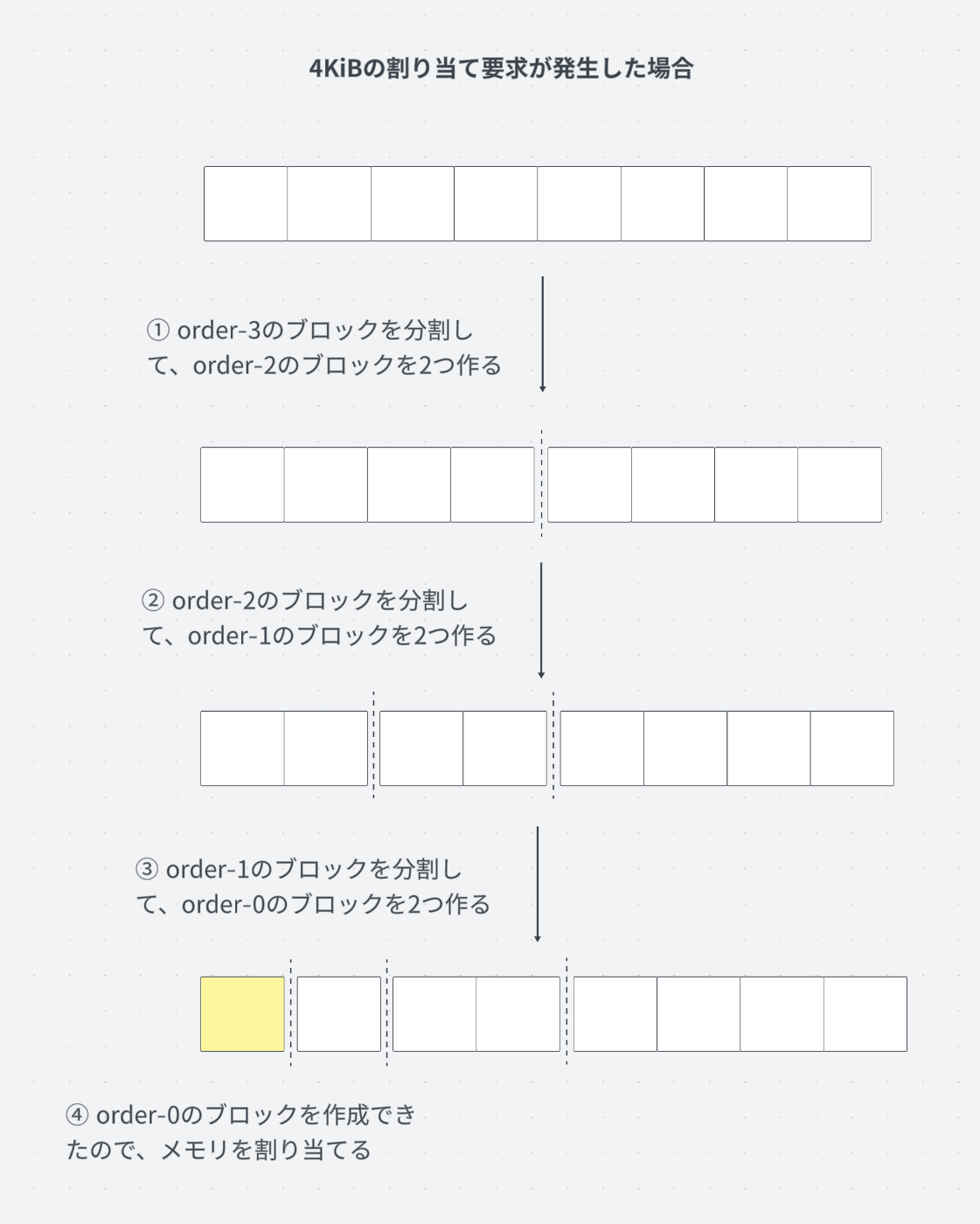
4KiBのメモリ割り当ての様子

この例は、4KiBのメモリ割り当てプロセスを示しています。
4KiBの要求なので、order-0のブロックを割り当てれば良いのですが、図ではorder-3のブロックしか存在していません。このような場合、Buddy Memory Allocationでは、利用可能なorder-nのブロックの分割してorder-(n-1)のブロックを2つ作成します。適切なサイズのブロック（ここではorder-0）が現れるまで再起的にこのプロセスを行います。

①では、order-3のブロックを分割してorder-2のブロックを2個作成しています。このようにあるブロックを分割したときに作られる2個のブロック同士はバディと呼ばれます。1個のブロックに対するバディは一つしか存在しません。このバディはメモリが解放される際に重要な役割を果たします。

②,③のステップで更に分割を行うと、必要なorder-0のブロックが現れるので、このブロックに対してメモリが割り当てられます。

更に8KiBのメモリ割り当て要求が来た場合、order-0のブロックを作る過程でorder-1のブロックが既に作成されているので、このブロックをそのまま割り当てることができます。

メモリの解放

次にメモリの解放のプロセスについて見ていきます。

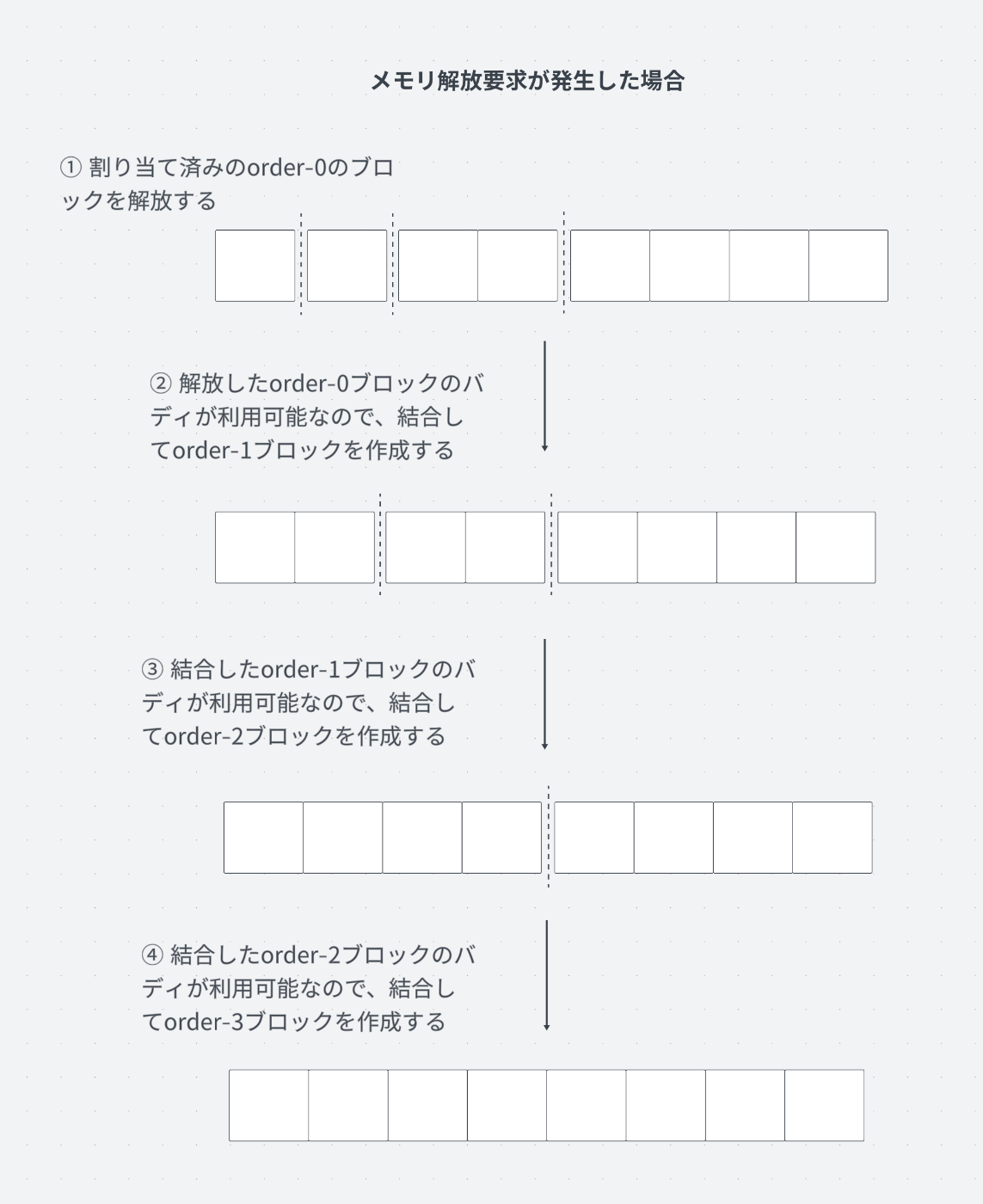
4KiBのメモリ解放を行う様子

この例では、先ほど割り当てた4KiBのメモリを解放するプロセスを示しています。
メモリの解放を行った後、解放したブロックのバディに当たるorder-0のブロックを確認します。このブロックが利用可能な状態であれば、バディ同士を結合してorder-1のブロックを作成します。
この結合のプロセスも、再起的に行われます。

②,③,④のステップでそれぞれ結合が行われ、最終的にorder-3のブロックが一つ作成され4KiBを割り当てる前の状態に戻りました。

このような管理方法がどのような利点を生み出すのかを考えていきます。

どのような利点があるのか

特徴的な割り当てと解放のプロセスによって、以下のような利点が生まれます。

外部フラグメンテーションの削減

ビットマップ方式のような連続的なメモリ割り当て方式で問題になる、外部フラグメンテーションの発生を減らすことができます。比較するために、ビットマップ方式とBuddy Memory Allocationを使用して割り当てと解放を行う例を示します。

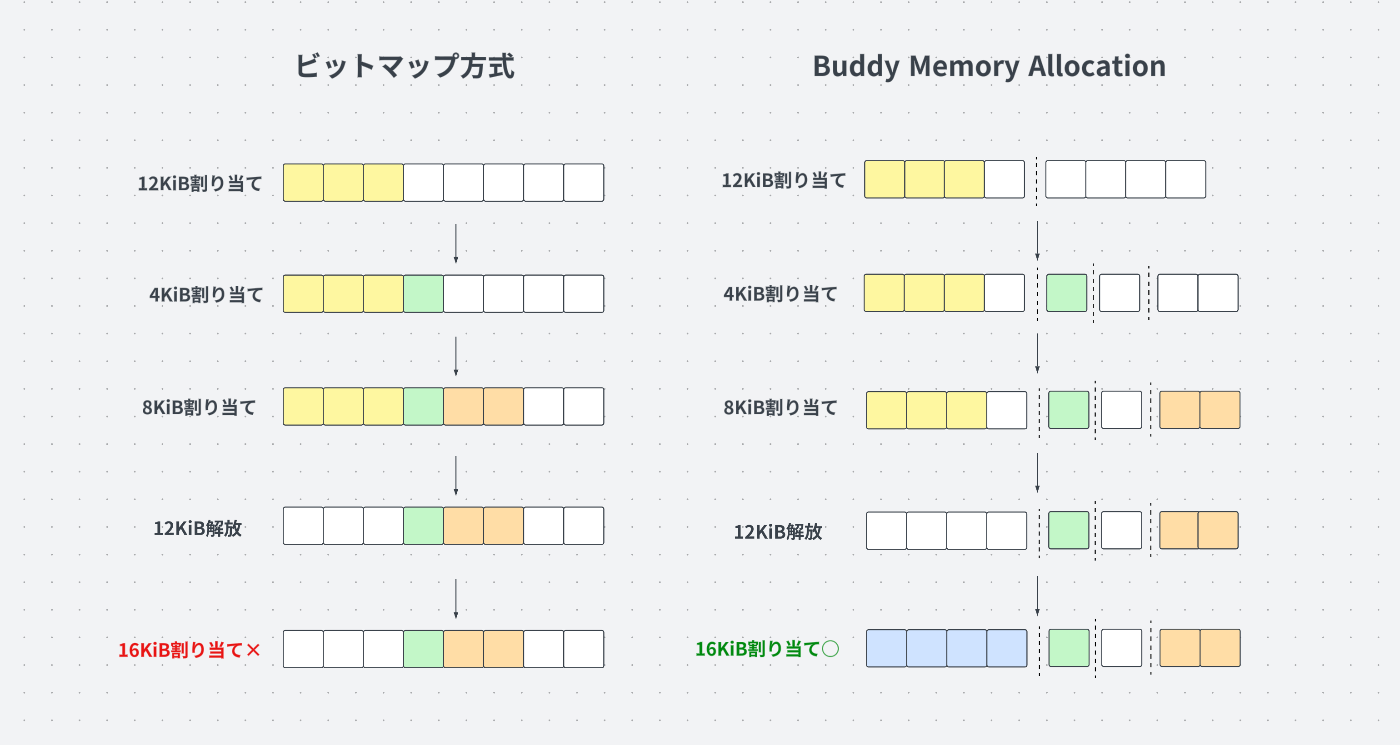
ビットマップ方式とBuddy Memory Allocationの比較

両者とも、割り当てと解放を同じ順序で行っていますが、ビットマップ方式では16KiB割り当ての際に外部フラグメンテーションが発生します。一方で、Buddy Memory Allocationでは外部フラグメンテーションが発生することなく16KiBのメモリを割り当てられています。

このように外部フラグメンテーションを削減することができるのには、以下の要因が考えられます。

要求されたサイズよりも大きなサイズを割り当てる可能性がある

Buddy Memory Allocationでは、要求されたサイズよりも大きなブロックのサイズを割り当てる可能性があります。上図の場合、12KiB割り当ての際に16KiB(order-2)のメモリブロックを割り当てているので、そのメモリ領域が解放された後に、より大きなメモリ割り当て要求にも柔軟に対応することができ、解放されたメモリ領域が他のメモリ要求に再利用されやすくなるというメリットがあります。

均一なブロックサイズを割り当てる

従来の連続的な割り当て方式では、異なるサイズのメモリ割り当てと解放が繰り返され、時間と共に様々なサイズの未使用領域が生じます。これが外部フラグメンテーションの原因となります。

しかしBuddy Memory Allocationを用いる場合、メモリブロックは常に2の冪乗の均一なサイズで割り当てられます。これにより、解放されたメモリブロックも2の冪乗のサイズであることを保証し、未使用のメモリが効率的に整理され、再利用されやすくなります。

動的に結合、分割を繰り返す

Buddy Memory Allocationでは、使用後のメモリが解放されると、未割り当てのバディと結合して大きなブロックを形成します。なので、長期間にわたって大量の小さな未使用ブロックが蓄積する可能性が低くなります。

高速な割り当てと解放

このアルゴリズムは、割り当てと解放を高速に行うことができます。
従来の連続的なメモリ割り当て方式では、都度空いているメモリを線形に探す必要があるのに対し、Buddy Memory Allocationでは利用可能なブロックの状態とサイズを事前に定義し、要求されたサイズに適したサイズのブロックを迅速に見つけることができるためです。

しかし、Buddy Memory Allocationは従来の連続的なメモリ割り当て方式とは異なり、要求されたサイズを超える最小の2の冪乗数のブロックを計算し、分割や統合の際にはバディのアドレスを特定する必要があります。
ですが、2の冪乗単位でブロックを割り当てるという制約のおかげで、これらの追加操作によるオーバーヘッドを最小限に抑えることができます。それぞれ詳しく見ていきます。

要求されたサイズに最適なorderの計算

最適なorderの計算は、割り当てや解放のたびに発生するので計算コストは重要になります。
2の冪乗単位でのブロック割り当ての利点を理解するために、3の冪乗単位と2の冪乗単位でのブロック割り当てのコード例を比較します。

// 3の冪乗単位の場合
int buddy_system::calculate_order(size_t size)
{
	const size_t num_pages = (size + PAGE_SIZE - 1) / PAGE_SIZE;
	
	int order = 0;
	while (std::pow(3, order) < num_pages) {
		++order;
	}

	if (order > MAX_ORDER) {
		return -1;
	}

	return order;
}

int bit_width(int x)
{
	if (x == 0) {
		return 0;
	}

	return CHAR_BIT * sizeof(unsigned int) - __builtin_clz(x);
}

int bit_width_ceil(int x)
{
	if ((x & (x - 1)) == 0) {
		return bit_width(x) - 1;
	}

	return bit_width(x);
}

// 2の冪乗単位の場合
int buddy_system::calculate_order(size_t size)
{
	const size_t num_pages = (size + PAGE_SIZE - 1) / PAGE_SIZE;
	
	const int order = bit_width_ceil(num_pages);

	if (order > MAX_ORDER) {
		return -1;
	}

	return order;
}

3の冪乗の場合、pow関数を用いたループ処理を行いますが、powは内部に浮動小数点の計算を含むため、整数計算よりもコストが高くなりがちです。

一方、2の冪乗の場合は、bit_width_ceilという関数を使用するだけでorderを求めることができます。この関数は与えられた数値のビット幅を返します。
与えられた数値を超える最小の2の冪乗の指数を知りたければ、その数値の2進数の幅（桁数）で求めることができます。
例えば、10を超える最小の2の冪乗の指数を求める場合、10は二進数で1010と表現され、その幅は4bitです。2^4は16であり、これは10を超える最小の2の冪乗となります。
これは、二進数の桁数が直接的に2の冪乗の指数と関連していることに基づいています。具体的には、与えられた数値が n ビットで表現できる場合、その数を超える最小の2の冪乗は 2^n となります。

このように、2の冪乗の場合は指数をより高速に求めることができます。

バディのアドレスの計算

バディのアドレス計算はブロックの分割や結合を行う際に求める必要があります。
これは、ブロックのアドレスxとそのサイズの指数kを用いて、バディのアドレスを次のように求めることができます。

$$buddy_k(x) = \begin{cases} x + 2^k & \text{if } x \mod 2^{k+1} = 0 \\x - 2^k & \text{if } x \mod 2^{k+1} = 2^k \end{cases}$$

アドレスxが、2^(k+1)（分割前のブロックサイズ）で割り切れる時、分割前のブロックサイズ境界でアラインされているということになります。
つまり、xがバディのアドレスよりも前に位置していることになるので、xに2^k（現在のブロックサイズ）を足せばバディのアドレスを求めることができます。
反対に、xを2^(k+1)で割った時の余剰が2^kであればバディのアドレスよりも後に位置していることになるので、xから2^kを引けばバディのアドレスを求めることができます。

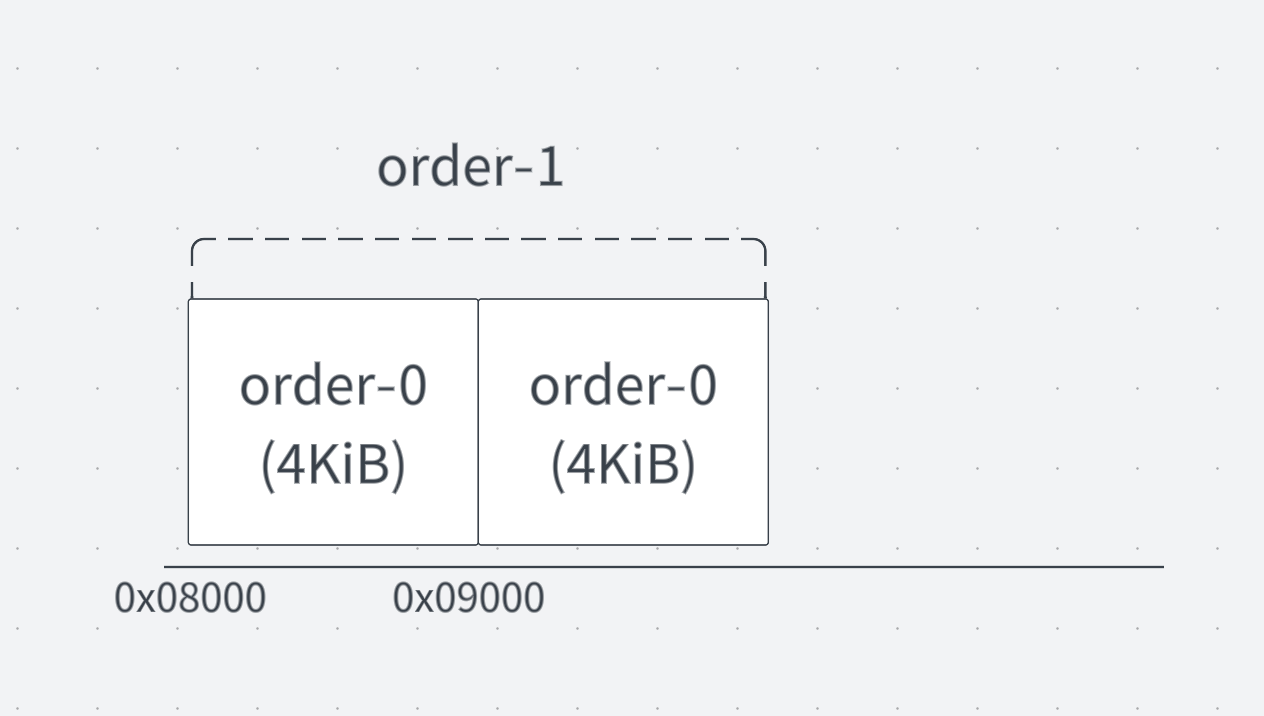
0x08000にブロックが配置されている
例えば、アドレスが0x08000のブロックのバディアドレスは、0x08000を8KiB (0x2000) で割った余剰が0のため、0x08000にブロックサイズを足して0x09000がバディのアドレスであることが求まります。逆に、0x09000のアドレスを0x2000で割った場合の余剰は0x1000(2^0)なので、ブロックサイズを引いて0x08000と求まります。

それぞれのアドレスを二進数に変換すると、以下のようになります。
0x08000 -> 1000000000000000
0x09000 -> 1001000000000000

つまり、バディのアドレス計算はアドレスの特定のビット（ブロックサイズ）を反転させる操作に相当します。これはXOR演算を用いて次のように求めることができます。

$$buddy_k(x) = x \oplus 2^k$$

ビット演算はハードウェアレベルで効率的に実行されるため、より高速に計算することができます。
このように、2の冪乗単位でブロックを割り当てることで、バディのアドレスの計算も効率的に行えるわけです。当たり前ですが、二進コンピューターと2のべきはやはり相性が良いですね。

問題点

Buddy Memory Allocationの利点を紹介してきましたが、もちろん問題点も存在します。4KiBのメモリブロックを最小単位としてメモリ割り当てを行いますが、例えば1KiBのメモリ割り当て要求が発生した場合でも、4KiBを確保して割り当てます。これによって3KiBのメモリが無駄になってしまいます。このような現象を内部フラグメンテーションと呼びます。

Linuxでは、この内部フラグメンテーションの発生を防ぐためにBuddy Memory AllocationとSlab Allocationを組み合わせて使用しています。これによってBuddy Memory Allocationで発生する内部フラグメンテーションの発生を最小限に抑え、より効率的なメモリ管理を実現します。

この辺りの話は、後編で詳しく解説しますのでご期待ください。

終わりに

Linuxのメモリ割り当てアルゴリズムである、Buddy Memory Allocationがどのようアルゴリズムなのかについて書きましたが、やっぱりアルゴリズムは面白いですね。
また、広く普及されている物がなぜ広く普及されているかを調べるのも良い勉強になるなと思いました。

参考

• Donald E.Knuth, The Art of Computer Programming Volume 1 Fundamental Algorithms Third Edition 日本語版, 2015
• https://www.kernel.org/doc/gorman/html/understand/understand009.html
• https://en.wikipedia.org/wiki/Buddy_memory_allocation