📚

50代になってから始めた数学の学び直しを振り返り、独習ノートを晒します。

2023/11/04に公開6件

math

1. はじめに

1.1 概要

50代になってから数学の学び直しを始めて、大学教養課程レベルの線形代数、微分積分、確率統計をいったん終えました。この記事はその振り返りです。

1.2 独習に使用したノートを晒します。

独習用の書籍に取り組むときに使ったノートを、後でどこからでもPCで見返せるようにしておくためにPDFにしてGoogle Driveに上げています。参考までにご覧下さい。
以下の表は、使用した書籍および各書籍について使用したノートの冊数、ノートをPDF化したものへのリンクを一覧にしたものです。上から順に取り組みました。(※各リンク先のPDFはファイルサイズが平均約20MB、最大約30MBですので、表示されるまで若干時間を要します。)

順番	独習に使用した書籍	冊数	PDF
1	線形代数イントロダクション	10	1#1　1#2　1#3　1#4　1#5　1#6　1#7　1#8　1#9　1#10
2	数研「大学教養微分積分」	19	2#1　2#2　2#3　2#4　2#5　2#6　2#7　2#8　2#9　2#10　2#11　2#12　2#13　2#14　2#15　2#16　2#17　2#18　2#19
3	マセマキャンパス・ゼミ「常微分方程式」	5	3#1　3#2　3#3　3#4　3#5
4	共立出版　数学ワンポイント双書「一様収束」	4	4#1　4#2　4#3　4#4
5	東海大学出版会「オイラーの贈物」	4	5#1　5#2　5#3　5#4
6	マセマキャンパス・ゼミ「確率統計」	4	6#1　6#2　6#3　6#4
7	東京大学出版会「統計学入門」	7	7#1　7#2　7#3　7#4　7#5　7#6　7#7

PDFを見返すと独習を始めた頃の線形代数のノートはほとんど殴り書きで、単に計算用紙としてノートを使っています。微分積分に入ると少しはましになってきますが、頭に入れたい概念の定義や定理の証明を何度も書き直したりしています。また独習ですから間違った理解を正しいと思い込んだまま証明を書いて、分かったつもりになっている箇所も少なからずありそうです。とまれ上記の表に挙げた各書籍に曲がりなりにも取り組んだことを示す、書証のつもりでノートを晒しました。

余談ですが、使用したノートは、PLUS の品番 NO-204GS (A4 G罫 5mm方眼 40枚) という方眼ノートです。また筆記用具は当初シャープペンシルを使っていましたが、「オイラーの贈物」からは万年筆に替えました。プラチナ#3776センチュリーUEF(超極細字)を使っています。

1.3 私について

本記事の作者であり学び直しをした本人である私は、以下の属性を持つ者です。

現在50代半ばの男性
日本国籍、母国語は日本語で、日本の学校で教育を受けた。
プログラミングは18歳から始めた。
現在はフリーランスで、ここ5年くらいは以下のような感じで現役プログラマーを続行中
- JavascriptやTypescriptのReactによるフロントエンド開発を主としてお請けし、
- Pythonだったらバックエンドも兼任したりもしつつ、
- 直近ではデータ分析チームにも所属し、主にNumPyやPandasなどを使って前処理を担当

1.4 この記事の目的

当方と同様に中高年になってから、あるいは社会人になってから数学を学び直したいと思っている、あるいは目下まさに学び直しの途上である方々の参考にして頂ければ幸いです。

2. 学び直しのきっかけ、方針など

2.1 数学を学び直そうと思ったきっかけ

高校生のときまで数学は得意な科目でした。とはいえ、この得意というのは受験勉強としての数学を上手くこなせていたのを得意がっていただけかもしれません。
社会人になり職業プログラマーになってからは業務システムの設計、開発をしばらくやり、その後フロントエンジニアが主業務となってきた中で、仕事の場では（大学レベルの）数学の能力を特段求められるという状況は、以下の3. まで殆どありませんでした。
2019年の秋、データ分析サービスを事業会社に提供する某企業さんから「データ分析した結果を今のところはJupyter Notebookで客先に見せているのだけれど、グラフだったりチャートだったりを、もっと効果的に視覚に訴えるようにUIデザイナーが設計したデザインの画面で見せられるWEBを作りたい」という案件にフロントエンジニアとして参画しました。
その業務は、正規分布の確率密度のグラフを描いたり、プロットされた点群の中に回帰直線を描いたりなどの、いわゆるデータビジュアライゼーションをUIデザイナーさんが設計し、それを元に私がReactでプロトタイプを作るという滑り出しでスタートしました。
その業務を進める中で、フロントエンド開発者の私にはデータ分析に使う数学の知識はマストなスキル要件ではありませんでしたが、事あるごとに「正規分布の確率密度ってどんな関数だっけ?（そもそも確率密度って何だっけ？)」とか、「回帰係数ってどうやって計算するんだっけ?」といったように、大学の教養課程レベルのことを忘れていることを自覚せざるを得ない状況があり、「自分の数学レベル、もしかしてかなりハズいのでは…」と冷や汗をかきました。それで「もう一度ちゃんと数学を勉強し直したいな」と思い始めたのでした。
そこで実際に本格的な独習に入る前に、まずはお試しという心づもりで、その年の11月からビッグデータ系の某講座を受講しました。それは「Python＋数学講座」というもので、次のステップである「機械学習講座」の受講に必要とされるPythonと数学について、最低限の知識と実践を習得するためのものでした。
この講座は週に1回で、全10回の講義がありました。その前半5回がPythonの基礎、後半5回が数学というコースでした。前半の最終回にはPythonについての修了試験、後半の最終回には数学の修了試験がありましたが、数学の修了試験で一問間違えてしまいました。間違えたのは確率統計の問題で、真陽性や偽陽性をちゃんと理解しているかが問われる問題でした。満点を取れなかったのが悔しくて、いよいよちゃんと勉強し直そうと思ったのでした。（世の中の状況としては、この全10回の講座が終わりに近づく頃、コロナ禍がいよいよ本格化して、どの会社でも勤務がリモートに移行し始めました。）

2.2 学び直しの方針

上述したとおり、きっかけとしてはフロントエンジニアの立場でデータ分析系のお仕事を支援させて頂いたことではあるのですが、学び直しをするにあたっては

今、巷で流行っているものの概要を把握するために必要最低限の数学をサクっと身につける、といった姿勢で取り組むのはやめよう

と決めました。学び直しをするなら、理工系の学部生向けに書かれた教科書を使って腰を据えて何にでも応用できるように基礎をしっかりやり、また独習する途上で興味の赴くまま寄り道にそれることも良しとする。これを基本方針としました。

2.3 実際に学び直しを始めた日

独習に使う書籍の一冊目「ストラング線形代数イントロダクション」を購入して取り組み始めたのは、本記事を執筆している現時点から約三年半前の2020年の4月からです。

2.4 どのような順で独習を進めたか

まずは線形代数から始めて、次に微分積分、そして確率統計の順に独習を進めました。

2.5 勉強のやり方とペース

   独習のやり方としては、各書籍を読み基本概念の定義や定理の証明を書き写したり、自分の言葉に替えて書き直したりして頭に定着させ、練習問題を解くといった極めてオーソドックスな方法です。
   分からないところを飛ばして先に進むといったことを出来るだけせずに、大事なことが書いてあると思ったら立ち止まり、ネットで深掘りして調べたり繰り返し書いてみたりといった愚直なやり方をしてきたので、ペースとしてはかなりゆっくり目です。
   また、学び直しを始めてから途切れなく数学の独習をし続けたわけではありません。たとえば確率統計の勉強をする際に、まず「マセマ確率統計」を終えてから、次の「統計学入門」に着手するまでの間、三ヵ月ほどは数学の独習をお休みして別のことをしていました。

3. 使用した書籍の振り返り

独習に使用した書籍

独習に使用した書籍は下記のとおりです。上から順に取り組みました。

線形代数

近代科学社「世界標準MIT教科書ストラング：線形代数イントロダクション」

微分積分

数研講座シリーズ「大学教養微分積分」
マセマ出版社キャンパス・ゼミ「常微分方程式」(改訂8)
共立出版　数学ワンポイント双書1 「一様収束」
東海大学出版会「オイラーの贈物」

確率統計

マセマ出版社キャンパス・ゼミ「確率統計」(改訂6)
東京大学出版会「統計学入門」(基礎統計学Ⅰ)

副読本・参考サイト

また、以下の書籍やWEBサイトも参考にしました。

数研出版チャート式シリーズ「大学教養微分積分」
近代科学社「スッキリわかる確率統計」
増訂解析概論
統計WEB

以下は、上記に挙げた各書籍についての振り返りや寸評です。

3.1 近代科学社「世界標準MIT教科書ストラング：線形代数イントロダクション」

版元の紹介ページ | Amazon

この本を選んだ経緯

数学の学び直しをしようと思ってから最初に取り組んだ本です。この本の目次は Amazon の「サンプルを読む」から確認できます。
理系学部の初年度に習う線形代数の独習本や参考書として良さそうな本を調べると、いくつも候補が得られます。それらの中からこの本を選ぶときに以下の手順を踏みました。
1. 候補になる書籍のAmazonのレビューを読んで自分に合いそうなものの候補を3, 4冊ほどに絞り込む。
2. 候補にあげた書籍の在庫がある書店に行き、実物にざっと目を通し「これでいこうかな」と思えたものに絞る。
3. 最後は値段で決めました。この本の価格は税別8,000円とかなりいいお値段ですが、数学の学び直しを始める第一冊目だったので、自分に発破を掛ける意味でもこれを選びました。

前半と後半の2パート構成

本書に取り組む際には大きく前半と後半の２つに分けて、まずは前半を終わらせるのをマイルストーンにするとよいかと思います。第1章からどこまでが前半かというと、まず序文のⅵページ目に以下の一文があります。

本書を2つの講義コースに分けるのなら、基礎コースの最後を特異値分解とし、また、続くコースでは特異値分解から始めることが多い。
特異値分解は本書第6章の最後の節6.7で出てきます。また本書の裏表紙にも以下のように書かれています。

多くの大学で（そして、今では高校でも）この教科書が採用されています。7〜10章の内容は、線形代数を使うより高いレベルにある学生に向けたものです。
上記をふまえて、第1章から6章までを前半とし第7章から最後までを後半とします。あるいは序文ⅳページ目に

第7章までの基礎コースの各節の終わりには挑戦問題がある。

　と書かれているので、第7章までを前半とするのでもよいでしょう。

本書の中核的な概念

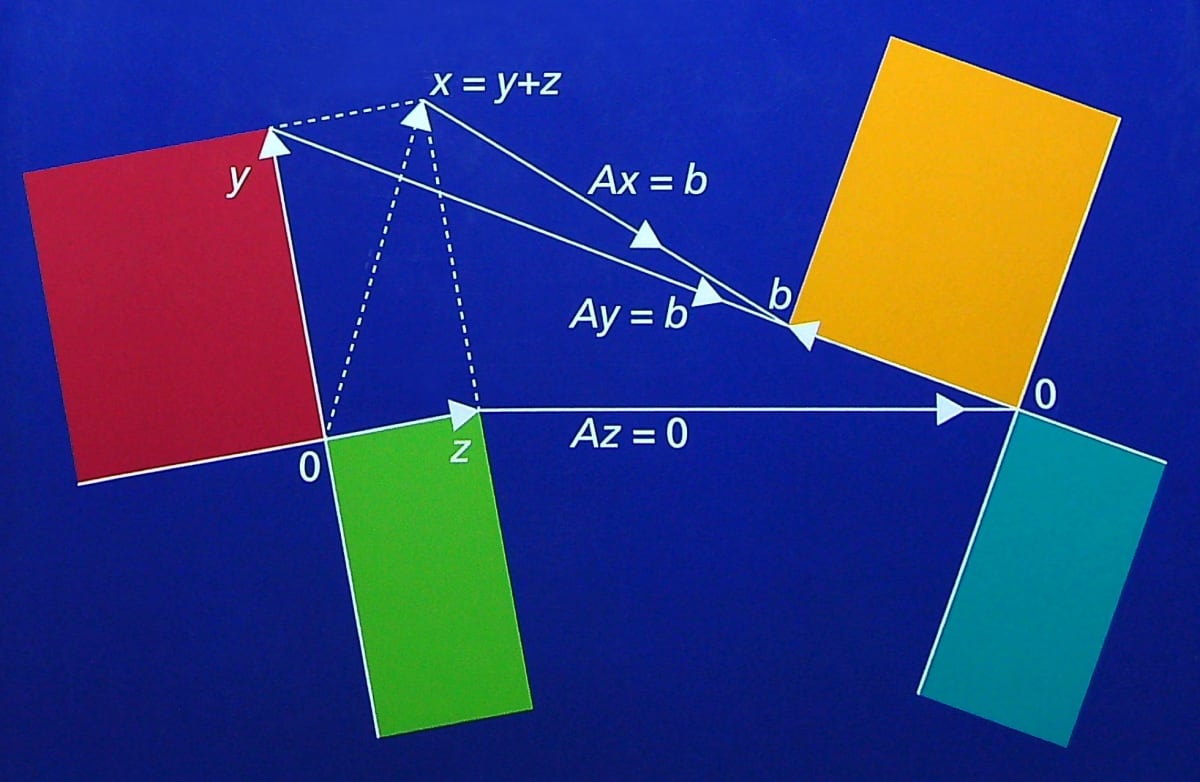
本書の前半の中でひとつの到達点となるのは、表紙にある下記の図です。

４つの基本部分空間

色のついた４つの四角形は本書の中核的な概念である４つの基本部分空間を表しています。これら４つの基本部分空間については以下の2つの節で説明されています。
- 3.6節「４つの部分空間の次元」
- 4.1節「４つの部分空間の直交性」

独習の進捗

独習の進捗ですが、以下のような状態で前半の第6章までを終わらせて、いったんこの本からは離れました。
- 第2章までは、説明文を読むだけではなく練習問題も解いていった。
- 第3章からは方針を変えて、基礎概念や定理などの理解にとどめ練習問題はやらずに進め、第6章までを読了した。
- 後半の第7章以降は未着手
本書は練習問題が良問揃いで、問題を解くために頭を使いノートの上に文字や式を書くのが楽しいので、ついつい深掘りしてしまいます。そうすると前半を終えるだけでもかなりの時間がかかってしまうと見積もって、第3章からは練習問題を解くのを保留にしました。
上記のとおり、第3章から第6章は練習問題をやってないのと後半(第7章以降)はまったくの手つかずで線形代数はひとまず終わりにして、微分積分に取りかかりました。このままこの本を放置してしまうのは未着手部分が多くてもったいないという心残りがあり、これらに取り組むのは優先順位の高い残タスクです。

こういう人にお勧め

この本はこういう人に適していると思う、という私見を述べます。理工系の学部生の一、二年生でこういう人はいませんか? (特に物理だったり電気だったりの、数学を道具として使う学科に進もうという学生の方）
- 学校指定の線形代数の教科書で勉強していて一応理解はできている(つもりではある）のだけれど、いまひとつ無味乾燥というのか面白みを感じない。面白みを感じないので頭に入ってこない

というあなたにこの本は良い刺激になるかもしれません。

上記にあてはまる人は、この本のまずは第1章と第2章(の出来れば全て。または少なくとも2.3節「行列を使った消去」まで）でよいので読み挑戦問題も含めて練習問題をやってみた後に、学校の教科書に戻って該当部分の説明を読むと「活きたイメージ」が見えてくるようになり、学校の教科書とこの本を行き来すれば線形代数が自分の武器になっていく手応えを感じられるのではと思います。(ただし手を動かして練習問題を解いていかないと、このような手応えはおぼつかないでしょう。)
プログラマーが本書を読んでいくと、「この手順をコードに書いてみたい」というアルゴリズムに出会うと思います。小生は 4.4節の「直交基底とグラム-シュミット法」を読んだあとコードを書きたくなって、QR分解をTypeScriptで書いてみるという趣旨の投稿を書いたりしました。

ストラング先生の語りかけ

ときどきこんな風にストラング先生が読者に語りかけます。

ぜひ最後まで取り組もう。本物の数学を行っているのだ。

（同著 3.6節「4つの部分空間の次元」 P.195 より引用）

ストラング先生の肉声で講義を聴きたくなったら、こういった動画で講義を視聴できます。(もちろん英語ですが)

先述の状態で「線形代数イントロダクション」からいったん離れて、次に微分積分に取り組みました。最も時間をかけた一冊は

数研講座シリーズ「大学教養微分積分」

です。この本を終えたあと、微積(解析)関連の各論で興味を持ったトピックが出てきたので、それらについての下記の3冊を上から順に取り組みました。

マセマ出版社キャンパス・ゼミ「常微分方程式」(改訂8)
共立出版　数学ワンポイント双書「一様収束」
東海大学出版会「オイラーの贈物」

以下、これらについて振り返ります。

3.2 数研講座シリーズ「大学教養　微分積分」

版元の紹介ページ | Amazon

微分積分の基本書として、この本を選んだ理由は下記の2点により独習に適していると考えたからです。
- レイアウトが高校の教科書と同じような体裁で馴染みやすい。
- 本書の練習問題と章末問題の解答が、別冊の「チャート式シリーズ　大学教養　微分積分」に掲載されており、一問につきだいたい1ページ、詳しい解答だと2ページ割かれているので、答え合わせに事欠かない。

振り返り

この本はかなりガチンコでやったという実感があります。使ったノートは19冊になりました。時間も約一年かかりました。
この本をしっかりやったことで、以下のような効果がありました。
1. この本を始める前は、この本を終えたら次に確率統計に取りかかろうと思っていましたが、この本を終えた時点で興味の惹かれる各論が出てきて寄り道をしたくなり、微分方程式、一様収束、オイラーの公式についての書籍を読みました。
  - 先述の 2.2 学び直しの方針に書いたように、「寄り道もまた良き」という考え方で今回の学び直しをしてきました。
2. 確率統計の独習のときに活かされました。
  - 確率統計に着手してからの一冊目、「マセマキャンパス・ゼミ　確率統計」に取り組んでいたときに、同著P.33「モーメント母関数をマスターしよう！」のところで
    
    微分積分の知識が不足している人は「微分積分キャンパス・ゼミ」(マセマ)で勉強しておくことを勧めるよ。確率・統計の学習に微分積分の知識は必要不可欠だからだ。

とありましたので、本書で微積をきっちりやっておいてよかった
と思いました。

本書の第7章「積分(多変数)」の「広義の重積分とその応用」の節で、ガウス積分

\int_{-\infty}^{\infty} e^{-x^2} dx

      の結果が $\sqrt{\pi}$ になることを導出するための諸概念の準備とそれらを使った導出手順、および
      この結果から標準正規分布および正規分布の確率密度関数が得られることを学びました。
         数学を学び直すきっかけのひとつであった「正規分布の確率分布がどんな関数だったか
      正確に覚えていない」という大問題が解消されて、ほっとひと息つけたのでした。

本書に出てくる定理で証明が省略されているものがあったので、増訂解析概論にあたって、当該定理の証明を参照しました。

3.3 マセマ出版社キャンパス・ゼミ「常微分方程式」(改訂8)

版元の紹介ページ | Amazon (※本記事の作成時点での最新版は改訂10)

3.2 数研講座シリーズ「大学教養　微分積分」の最後の章が「第9章微分方程式」だったのですが、割かれている紙面が約20ページほどだったので、もう少し詳しく知りたいと思ってこの本に取り組みました。

3.4 共立出版数学ワンポイント双書 1 「一様収束」

版元の紹介ページ | Amazon

先の3.2 数研講座シリーズ「大学教養　微分積分」の第8章は「級数」なのですが、この章の中で「整級数で与えられる関数の連続性」についての定理があります（同著P.304 定理2-3）。これを証明するときの第一段階として、所与の整級数の部分和で与えられる多項式関数を項とする関数列がある条件を満たすことを証明します。この条件というのが一様収束性でした。また一様収束はしないが各点では収束する場合もあり、この両者の違いが大きいということも知りました。
復習も兼ねて詳述すると、区間 $I$ 上で定義されたある関数列 $\{f_n\}$ が(a)各点収束する、あるいは (b) 一様収束する条件は(「大学教養　微分積分」P.309によれば、)それぞれ以下
- (a) $\forall a \in I, \forall \epsilon >0, \exists N \in \mathbf{N}\hspace{1mm} such\hspace{1mm}that\hspace{1mm}\forall n\in\mathbf{N}\hspace{1mm}(n\geqq N\Rightarrow |f(a) - f_n(a)| < \epsilon)$
- (b) $\forall \epsilon >0, \exists N \in \mathbf{N}\hspace{1mm} such\hspace{1mm}that\hspace{1mm}\forall a \in I, \forall n\in\mathbf{N}\hspace{1mm}(n\geqq N\Rightarrow |f(a) - f_n(a)| < \epsilon)$

であり、両者は $\forall a \in I$ の位置が異なるだけですが、その意味するところの違いが大きく、
一様収束という概念（の意味するところの強さ）に興味を持ちました。

そこで一様収束に論点を集中させた本書を入手して読みました。この本は以下の3つの問題A,B,Cの提起から始まります。

(以下、同著P.3〜4から引用)

問題A
「区間 $I$ で定義された関数 $f_n(x)$ からなる関数列 $\{f_n(x)\}$ は関数 $f(x)$ に収束するとする。各関数 $f_n(x)$ が連続ならば、極限関数 $f(x)$ も連続であるか?」

問題B
「閉区間 $[a,b]$ で定義された関数 $f_n(x)$ からなる関数列 $\{f_n(x)\}$ は関数 $f(x)$ に収束するものとする。各関数 $f_n(x)$ と極限関数 $f(x)$ が連続ならば、定積分 $\int_{a}^{b} f_n(x) dx$ からなる数列 $\{\int_{a}^{b} f_n(x) dx\}$ は定積分 $\int_{a}^{b} f(x)dx$ に収束するか? いいかえると関係式

\lim_{n \to \infty} \int_{a}^{b} f_n(x) dx = \int_{a}^{b} f(x) dx = \int_{a}^{b} \lim_{n \to \infty} f_n(x) dx

が成り立つか?」

問題C
「区間 $I$ で定義された関数 $f_n(x)$ からなる関数列 $\{f_n(x)\}$ は関数 $f(x)$ に収束するとする。各関数 $f_n(x)$ が微分可能ならば、極限関数 $f(x)$ も微分可能で、導関数 $f^{\prime}_n(x)$ からなる関数列 $\{f^{\prime}_n(x)\}$ は導関数 $f^{\prime}(x)$ に収束するか? いいかえると関係式

\lim_{n \to \infty} f^{\prime}_n(x) = f^{\prime}(x) = \big\{ \lim_{n \to \infty} f_n(x) \big\}^{\prime}

が成り立つか?」

(引用ここまで)

次に上記の問題A,B,Cに対して反例が示された後、「一様収束」が定義され、上記A,B,Cの各問題に所与の関数列の収束が単なる(各点)収束ではなく一様収束を満たすという前提を付加することで、各問題を定理に進化させていくという議論が展開されます。素人な言い方ですが「数学してる感」を味わえました。
本書にはルベーグ積分について少しだけ触れている箇所があり、今後のどこかでルベーグ積分を学びたいというモチベーションも得られました。

3.5 東海大学出版会新装版「オイラーの贈物 ─ 人類の至宝 $e^{iπ}=−1$ を学ぶ」

版元の紹介ページ | Amazon

(※私の手元にあるものの版元は「東海大学出版部」となっていますが、今現在は「東海教育研究所」が版元となっているようです。)

数学の学び直しを始めるよりもずっと(一年以上)前に購入したものの読み始めるタイミングがなく積ん読になっていましたが、先述の数研講座シリーズ「大学教養　微分積分」を読了したのを機に「今こそ読もう」と思って取り組み始めました。
オイラーの公式自体を導くところは $\cos θ$ と $\sin θ$ および $e^{iθ}$ を級数展開することで導出していますが、そこに至るまでの基本事項の積み上げにこの本の価値があります。基礎事項の確認で「大学教養　微分積分」を読み返すこともたびたびあり、よい復習になりました。
この本の最後のほうでフーリエ級数が出てきましたので、プログラムを書いて画面で確かめたいと思い、三角関数の様々な和を作って波形をSVGで描画して、無限に足し合わせていくとある波形に収束していく様を確認するというお遊びをReactで作ったりしました。

上記までで、線形代数と微分積分を完了とし、次に確率統計に着手しました。取り組んだのは下記の2冊です。

マセマ出版社「確率統計キャンパス・ゼミ」改訂6
東京大学出版会「統計学入門」（基礎統計学Ⅰ）

また「統計学入門」を読み進めていく中で下記の書籍やWEBサイトを随時参考にしました。

近代科学社「スッキリわかる確率統計」
統計WEB
数学の景色
高校数学の美しい物語
- ヴァンデルモンドの畳み込みの証明を探していたときに助かりました。
PDF: 負の二項分布 (緑川章一青森大学名誉教授)
- 「統計学入門」6.4節に出てくる「負の二項分布」の「負の」とはどういう意味合いなのかモヤモヤしていたときに見つけてハラオチした資料です。

以下、上記に上げた書籍について振り返ります。

3.6 マセマ出版社「確率統計キャンパス・ゼミ」改訂6

(※この記事を作成している時点での最新版は改訂8)

版元の紹介ページ | Amazon

統計学を独習する際に、どのような本を選べばよいか？を調べると、東京大学出版会「統計学入門」（基礎統計学Ⅰ）が定番として挙げられていることが多いですが、一冊目から「統計学入門」から始めるのはハードルが高そうと思われたので、「統計学入門」を読む前の準備としてまずはマセマの本書に取り組みました。
確率統計の一冊目としてこれを選んだ理由は、微分積分の勉強中に「マセマ常微分方程式」を読んで、文体（筆者の語り口調）が頭に入ってきやすかったことです。
線形代数と微分積分の準備に時間をかけたことが活きて、マクローリン展開やベータ関数、正規分布の確率密度関数などを使うところで数学的な導出手順ではつまづくことがなかったので、その分、期待値や分散、共分散、さらには最尤推定量、検定といったように次々と出てくる確率統計の用語を把握、理解することに集中できました。

3.7 東京大学出版会「統計学入門」（基礎統計学Ⅰ）

版元の紹介ページ | Amazon

「確率統計キャンパス・ゼミ」を終えた後、定番の本書「統計学入門」に取り組みました。
掲載されている各種調査のデータが古いのは否めませんが、以下の2点のバランスがよかったです。
- 文系、理系共通の教科書であることに違わず、確率統計を勉強した先に（社会調査だったり、医学だったりの現場で）統計を駆使した実務があることを感じさせる説明が多くみられる。
  - より詳しく統計を駆使する現場で必要になる知識を求めるのであれば、同じシリーズの「Ⅱ 人文・社会科学の統計学」や「Ⅲ 自然科学の統計学」に進めばよいというシリーズ構成もうまく出来ていると思いました。
- それでいて、「第8章大数の法則と中心極限定理」までの数学的な基礎を固める章はきっちりと必要十分に書かれていました。証明が省略されているところもありますが、これは「証明を追いたいなら自分で調べてね」というメッセージであると解釈しました。
各章の練習問題で何らかの値を算出するものについては、まずは電卓と巻末の数表を使って算出し、その後Pythonのscipy.statsなどを使って検算し、手計算で出した値と比較して確かめるといったこともやりました。
良書であることは間違いないのですが、時間をかけての一度の通読だけでは頭に定着したとは言い難く、放っておくと忘れてしまいそうなので、今後も機会を作って読み返したいです。

3.8 近代科学社「スッキリわかる確率統計」

版元の紹介ページ | Amazon

東京大学出版会「統計学入門」を読み進める中で証明が省略されている箇所があり、そこを知りたいときにこの本には証明が載っているということがあったので副読本として手元に置き、随時参考にしました。

4. 今後について

次に何に取り組むかはまだ決めていませんが、避けたいのは、数学自体を嫌いになったり飽きたりしてしまうような課題や計画、目標、勉強の仕方をうっかり自分に課してしまって、無用なプレッシャーを感じて燃え尽き症候群になってしまうことです。
業務で求められるスキル習得に時間を割かないといけない期間もあるのでうまくバランスをとりながら、今後もボチボチやっていこうと思っています。お読み頂き、ありがとうございました。