⏲️

RWKVを論文と実装から読み解く

2023/06/06に公開

RWKVとは

昨今GPTをはじめとしたtransformerベースの大規模言語モデルが流行しています．transformerの重要な要素であるSelf-Attentionは，長距離の依存関係を学習するできるというメリットがある一方で，シーケンス内のすべての要素と他のすべての要素との依存関係を計算するために，計算量とメモリ使用量がシーケンス長の二乗（つまり、トークンの数の二乗）に比例してしまうという問題があります．

一方でRNNベースのモデルは，メモリと計算要件の面で線形にスケールしますが、並列化と拡張性の制限からtransformerと同等の性能を達成することが困難です．

そこで，transformerの効率的な並列学習と，RNNの効率的な推論の両方を兼ね備えたモデルとしてRWKV（Receptance Weighted Key Value）という新たなモデルアーキテクチャーが提案されました．

このモデルは，数百億のパラメータまでスケールする初の非Transformerアーキテクチャでありながら，同じサイズのTransformerと同等の性能を発揮することが論文内で示されています．

現在，GPTをはじめとしたtransformerベースのモデルよりも高速に推論可能なモデルとして注目されているRWKVの詳細を本記事で解説していきます．

RWKVの概観

まずは，RWKVのアーキテクチャーを眺めてみます．左がtransformerで右がRWKVです．

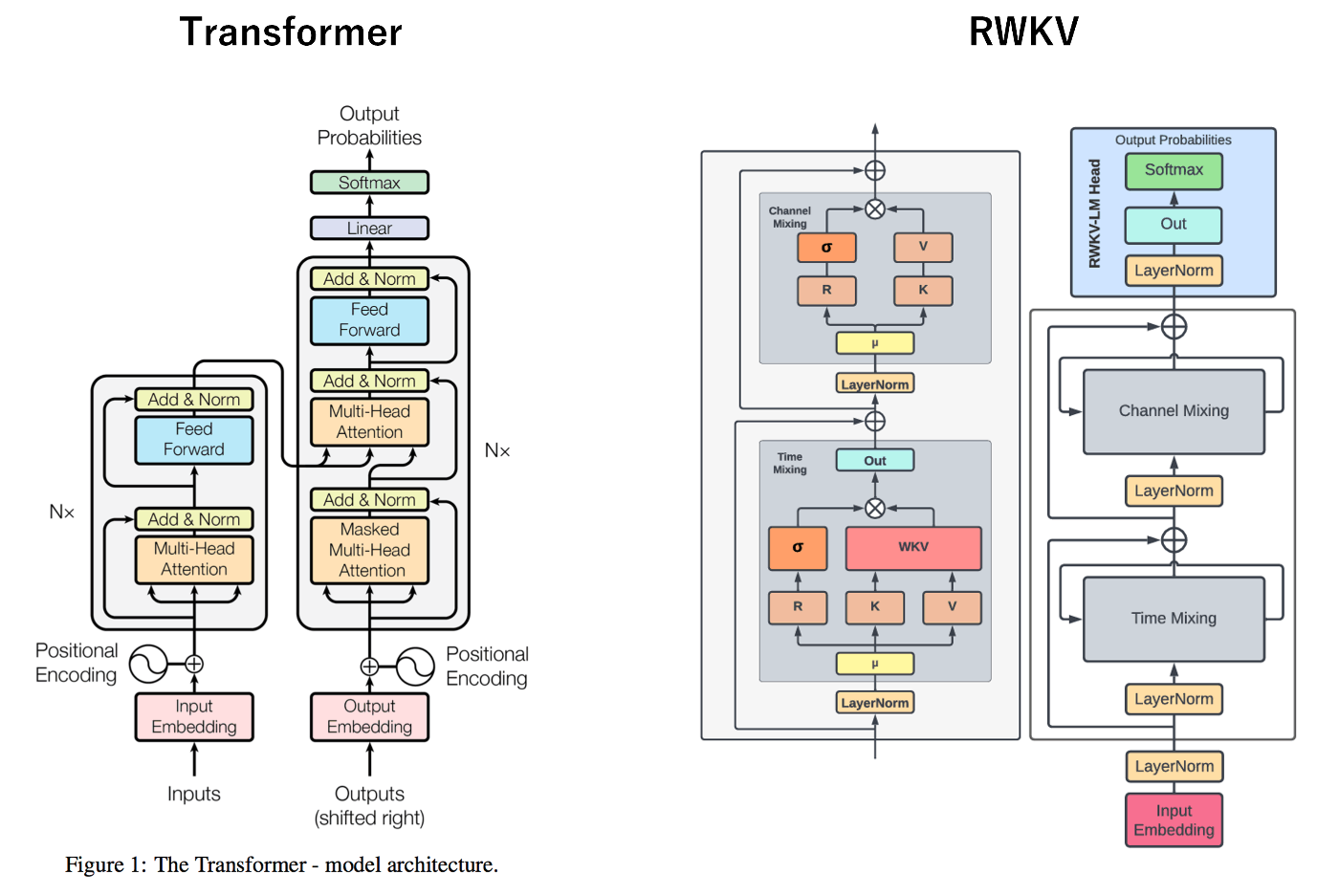
上図より，RWKVの特徴として，Time-mixing blockと，Channel-mixing blockがあることが分かります．RWKVは，transformerと違ってencoder-decoderモデルではない点は大きく違いますが，モデルの概観は似ていることもわかります．しかし，このTime-mixing blockの中身はmultihead attentionとは異なっており，その違いを理解することがRWKVの理解につながります．

RWKVの詳細：Time-mixingとChannel-mixing

RWKVは2つの主要なブロック，すなわちTime-mixing blockとChannel-mixing blockから構成されています．また，RWKVは，Time-mixingブロックとChannel-mixingブロックで使用される4つの主要なモデル要素から名前を取っています．

R：過去の情報の受容度を表現するReceptanceベクトル。
W：位置の重み減衰ベクトル。訓練可能なモデルパラメータ。
K：一般的な注意機構におけるK（Key）に類似のベクトル。
V：一般的な注意機構におけるV（Value）に類似のベクトル。

これらの解説に入る前に，まず一般的なtransformerと，先行研究であるAn Attention Free Transformerというモデルから紹介します．

先行研究: TransformerとAn Attention Free Transformer (AFT）

一般的なSelf-Attentionメカニズムは以下の数式で表されます．

\text{Attention}(Q, K, V) = \text{softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right)V,

ここで，Q，K，Vはクエリ（Query），キー（Key），値（Value）を示し， $d_k$ はキーの次元数， $N$ はシーケンスの長さ（つまりトークンの数）， $d_v$ は値の次元数を示しています。ちなみに，self-attentionではすべてのQueryベクトルとKeyベクトルの間で内積を計算しており，この操作が計算量がn^2になる主な要因です．

話は変わりますが，2021年にZhaiらによってAn Attention Free Transformer (AFT）が提案されました．この研究では，従来のTransformerモデルとは異なり，Self-Attentionメカニズムを使用せずに，代わりに全結合層（Fully Connected layer）を使用することを提案しています．これにより，計算コストを大幅に削減しながら，Transformerと同等またはそれ以上のパフォーマンスを達成することが可能となることを示しました．このAFTは以下の数式で表されます．

\text{Attn}^+(W, K, V)_t = \frac{\sum_{i=1}^t e^{wt,i + k_i} v_i}{\sum_{i=1}^t e^{wt,i + k_i}}

ここで， ${\omega_{t,i}} \in R^{T×T}$ は，学習されたペアワイズの位置バイアスを表しています．

RWKVは，上記のAFTに大きく影響を受けており，RWKVでは $\omega_{t,i}$ をチャネルごとの時間減衰ベクトルとして定義します．

\omega_{t,i} = - (t - i)\omega,

Time-mixing block

では，time-mixing blockの中身を見ていきましょう．まず3つの登場人物， $r_t, k_t, v_t$ から見ていきます．これらは以下の式で表されます．

r_t = W_r \cdot (\mu_r x_t + (1 - \mu_r) x_{t-1}), \\ k_t = W_k \cdot (\mu_k x_t + (1 - \mu_k) x_{t-1}), \\ v_t = W_v \cdot (\mu_v x_t + (1 - \mu_v) x_{t-1}), \\

上式は，時刻tにおけるReceptanceベクトルと，key, valueをそれぞれ表しています．また $µ_r$ は，時刻tにおける更新の割合を制御するパラメータで，0と1の間の値を取ります． $µ_r$ が大きいほど新しい入力 $x_t$ の影響が強く， $µ_r$ が小さいほど過去の状態 $x_{t-1}$ の影響が強くなります．
ちなみに，このとき新しい入力と過去の状態との間で線形補間を行うことで、再帰的な更新を行うことを可能にしています．

続いて，これらを使った演算の詳細を以下に示します．

w k_v t = \frac{\sum_{i=1}^{t-1} e^{-(t-1-i) w + k_i} v_i + e^{u + k_t} v_t}{\sum_{i=1}^{t-1} e^{-(t-1-i) w + k_i} + e^{u + k_t}}, \\ o_t = W_o \cdot (\sigma(r_t) \odot w k_v t). \\

こちらの式は，An Attention Free Transformer (AFT）と類似していることがわかります． $wkv_t$ は， $Attn(Q, K, V)$ と同じ役割を果たしまていますが，Q，K，Vの各要素がスカラーであるため二次のコストが発生しないところがミソです．

直感的には，時間tが増加するにつれてベクトル $o_t$ は長い履歴に依存するようになります．また，ターゲットポジションtに対して，RWKVは位置間隔[1, t]での加重平均を実行し，その後レセプタンスσ(r)と乗算します．したがって，インタラクションは与えられたタイムステップ内で乗算され，異なるタイムステップで合計されます．

これは、標準的なトランスフォーマーモデルが全てのトークンペア間でアテンションを計算するのに対し，AFTは過去の時間ステップ全てにわたる加算の形でアテンションを計算するという違いがあります．これにより，計算とメモリの効率性が向上していると考えられます．

ここで，RWKVの実装の一部を見てみます．実装はこちらのリポジトリから引用しています．

Time-mixing blockの実装

class RWKV_TimeMix(nn.Module):
    def __init__(self, config, layer_id):
        super().__init__()
	# configを省略
        # time_decayの初期化を省略

        self.time_shift = nn.ZeroPad2d((0, 0, 1, -1))
        with torch.no_grad():  # init to "shift half of the channels"
            ww = torch.ones(1, 1, config.n_embd)
            for i in range(config.n_embd // 2):
                ww[0, 0, i] = 0
        self.time_mix = nn.Parameter(ww)

        self.key = nn.Linear(config.n_embd, attn_sz, bias=False)
        self.value = nn.Linear(config.n_embd, attn_sz, bias=False)
        self.receptance = nn.Linear(config.n_embd, attn_sz, bias=False)

        self.output = nn.Linear(attn_sz, config.n_embd, bias=False)

        self.key.scale_init = 0
        self.receptance.scale_init = 0
        self.output.scale_init = 0

    def forward(self, x):
        B, T, C = x.size()
        x = x * self.time_mix + self.time_shift(x) * (1 - self.time_mix)
        k = self.key(x).transpose(-1, -2)
        v = self.value(x).transpose(-1, -2)
        r = self.receptance(x)

        # RWKV_K_CLAMP can be removed if the CUDA kernel substracts the correct k_max for each k (I will do this later)
        k = torch.clamp(k, max=RWKV_K_CLAMP)
        k = torch.exp(k)
        kv = k * v

        self.time_w = torch.cat(
            [torch.exp(self.time_decay) * self.time_curve, self.time_first], dim=-1)
        w = torch.exp(self.time_w)

        wkv = TimeX.apply(w, kv, B, C, T, 0)
        # RWKV_K_EPS can be removed if the CUDA kernel sets 0/0 = 0 (I will do this later)
        wk = TimeX.apply(w, k, B, C, T, RWKV_K_EPS)

        rwkv = torch.sigmoid(r) * (wkv / wk).transpose(-1, -2)
        rwkv = self.output(rwkv)
        return rwkv

時刻tにおける入力の更新割合 $µ_r$ はself.time_mixで表されています．また時刻 $t-1$ の入力xは，nn.ZeroPad2dを用いて表されています．これらを用いて入力xは，x = x * self.time_mix + self.time_shift(x) * (1 - self.time_mix)と実装され，過去の情報（時間的にシフトした部分）と現在の情報（シフトしていない部分）を適切な比率で混合した値へと変換されています．

Channel-mixing block

続いてchannel-mixing blockを見ていきます．こちらは以下の式で表されます．

r_t = W_r \cdot (\mu_r x_t + (1 - \mu_r) x_{t-1}), \\ k_t = W_k \cdot (\mu_k x_t + (1 - \mu_k) x_{t-1}), \\ o_t = \sigma(r_t) \odot (W_v·max(k_t,0)^2),

こちらはTime-mixing blockと比較するとシンプルです．Time-mixing blockが，異なる時間ステップのトークン間の相互作用を管理していたのに対し，Channel-mixing blockは，同じ時間ステップ内の異なるチャンネル（または特徴）間の相互作用を管理しています．Channel-mixing blockに関しては，よく使われる全結合層や畳み込み層といったものと同じ働きをしています．
ちなみに， $\sigma$ はsquared ReLUを使用し，直観的には「忘却ゲート」の役割を果たしています．

Channel-mixing blockの実装をいかに添付しています．こちらの実装は，Time-mixing blockが理解できれば容易に理解できると思います．

Channel-mixing blockの実装

class RWKV_ChannelMix(nn.Module):
    def __init__(self, config, layer_id):
        super().__init__()
        self.layer_id = layer_id

        self.time_shift = nn.ZeroPad2d((0, 0, 1, -1))

        with torch.no_grad():  # init to "shift half of the channels"
            x = torch.ones(1, 1, config.n_embd)
            for i in range(config.n_embd // 2):
                x[0, 0, i] = 0
        self.time_mix = nn.Parameter(x)

        hidden_sz = 4 * config.n_embd
        self.key = nn.Linear(config.n_embd, hidden_sz, bias=False)
        self.receptance = nn.Linear(config.n_embd, config.n_embd, bias=False)
        self.value = nn.Linear(hidden_sz, config.n_embd, bias=False)

        self.value.scale_init = 0
        self.receptance.scale_init = 0

    def forward(self, x):
        x = x * self.time_mix + self.time_shift(x) * (1 - self.time_mix)

        k = self.key(x)
        k = torch.square(torch.relu(k))
        kv = self.value(k)

        rkv = torch.sigmoid(self.receptance(x)) * kv
        return rkv

RWKVの特徴

RWKVの特徴として，学習時は「time-parallel mode (時間パラレルモード)」が使用され，推論時（デコード時）は「time-sequential mode (時間シーケンシャルモード)」が使用されます．

時間パラレルモード

時間パラレルモードは，そのままの意味で，時刻に関連する演算を並列して行うことです．これは，Time-mixing blockで紹介した新しい入力と過去の状態との間で線形補間を行う処理によって実現が可能となっています．これにより，各タイムステップの計算が他のタイムステップの計算から独立に行えるようになりました．
以上から，RNNでは実現できなかった並列処理がRWKVでは可能となっています．

時間シーケンシャルモード

学習時とは異なり，推論時にはRNNのような順次的なデコーディングを行います．このときRWKVはRNNのような構造を活用して動作し，これを時間シーケンシャルモードと呼んでいます．具体的には，各ステップの出力が次のステップの入力として用いられRWKVは出力トークンを一度に1つずつ生成します．つまり，あるトークンの生成は前のすべてのトークンの生成が完了した後に行われます．
これにより，RWKVはシーケンスの長さに関係なく一定の速度とメモリフットプリントを維持し，長いシーケンスを効率的に処理することができるようになります．
一方で，アテンションメカニズムを使用した場合はシーケンスの長さに比例してキャッシュの使用量が増加，シーケンスが長くなるにつれてメモリフットプリントと時間が増加します．
以上から，Transfromerでは実現できなかった効率的なデコーディングがRWKVでは可能となっています．

RWKVの評価

ようやく評価の話まで来ました．RWKVの論文では以下の質問に対して答えるための評価をしています．

RQ1: 同じパラメータ数とトレーニングトークン数を持つ二次元transformerアーキテクチャと比較して，RWKVは競争力があるか？
RQ2: パラメータ数を増やすと，RWKVは二次元transformerアーキテクチャとの競争力を維持するか？
RQ3: RWKVのパラメータ数を増やすと，より良い言語モデリングの損失が得られるか？特に，一般に公開されている二次元transformerが効率的に処理できないコンテキスト長でRWKVモデルを訓練する場合はどうなるか？

まず，RQ1とRQ2に対しては，以下の図を参照してください．これより，既存のtransformerモデルに対して非常に競争力があることが分かります．さらに，RWKVはPIQA，OBQA，ARC-E，COPAの4つのタスクでPythiaとGPT-Neoを上回っています．

ゼロショット性能の比較

また，以下の図より，コンテキストの長さを増やすとPileデータセットを使用したテストで損失が低くなることが示されており，RWKVが長いコンテキスト情報を効果的に利用できることが示されました．

context lengthの増加と損失の関係

RWKVを使う

RWKVの実装は以下のリポジトリで公開されています．

また，記事中のpython実装は上記リポジトリの以下のファイルを参照しました．

さらに，RWKVはhugging faceにも登録されているため手軽に試すことができます．

RWKVで推論する記事もいくつか上がっているため参考になると思います．
https://note.com/npaka/n/n97d8e48c8b80

まとめ

今回の記事では，RWKVの論文を解説しました．LLMを実利用する上では推論速度が一つの課題となっています．RWKVはLLMでありながらも効率的なデコード手法によって，Transformerモデルと比較して高速に推論することができます．LLMの実利用に向けて，RWKVはますます注目されていく技術だと思っています．今後の発展に期待したいと思います．

参考文献

記事の中の図に関しては，論文から引用しています．
https://arxiv.org/abs/2305.13048
https://arxiv.org/abs/2105.14103