本記事の目的
数理最適化の枠組みを用いて「告白してきた相手を受け入れるか拒否するか」の合理的な意思決定について分析します。完全にネタ記事なので、エンタメだと思ってお楽しみいただければと思います。ちなみにここで取り扱う理論モデルは経済学で応用されているサーチ理論の枠組みをそのまま利用したものとなります。この記事を通じて、経済学の思想を感じていただけたり、多少数学の勉強になれば大変嬉しいなぁと、著者は思っています。
数学的な展開に興味のない人は、前提条件だけ読んでいただいたら結論まで読み飛ばしていただいて構いません。
前提条件(物語の設定)
鈴木(もちろん架空の人物です)さんは恋人探し中です。とはいっても鈴木さんは自分から告白するということはないです。鈴木さんがすることは自分に対して告白してきた相手を受け入れるか受け入れないか、というたった一つの意思決定を行うことだけなのですから。
鈴木さんは自分の元に、自分に恋人がいない限り毎週 \alpha \in (0,1) の確率で告白してくれる相手が現れること、さらには最大でも週に告白してくる相手は一人であることが分かっています。また、鈴木さんの元にはいろいろな魅力を持った人々が告白してきます。鈴木さんにとって告白してきた相手の魅力度を \theta と置くことにしましょう。もし魅力度 \theta の人と付き合っている場合、鈴木さんは \theta の幸福度を毎週感じることになります。一方で、誰とも付き合っていない場合は b の幸福度を得られると仮定しましょう。
また鈴木さんは今までの経験から、自らの元に告白してくる人たちの魅力度の分布について完全に理解しています(恐ろしい経験量ですね。)。ここではその下限を \underline{\theta}、上限を \bar{\theta} と表し、その確率密度関数を f(\theta)、対応する累積型分布関数を F(\theta) と置くことにしましょう。さらに、この分布が常に不変であると仮定します。また、パラメータの条件として \underline{\theta} < b < \bar{\theta} を仮定します。この仮定は「鈴木さんにとって付き合っていないほうがまだ幸せな相手」が世の中に存在することを意味しています。
さらに、せっかく付き合ったとしても分かれてしまう確率があります。鈴木さんが別れてしまう確率はどんな相手と付き合っていたとしても毎週 s \in (0,1) の確率であり、そのことを鈴木さんは経験上理解していることとします。
また残念なことに、鈴木さんには寿命があります。ここでは単純化のため、毎週 \delta \in (0,1) の確率で鈴木さんは寿命を迎えてしまうことを仮定し、さらにはそのことを鈴木さんが熟知していることを仮定しましょう。
念のため、ここまでに登場したパラメータをまとめておきます。
パラメータの一覧
-
\alpha \in (0,1)
-
\theta \in [\underline{\theta}, \bar{\theta}]
- 鈴木さんにとっての相手の総合的な魅力度。
- 魅力度は確率変数であり、確率密度関数が f(\theta), 累積型分布関数は F(\theta) で表現される。
-
b \in (\underline{\theta}, \bar{\theta})
- 誰とも付き合っていない場合に得られる幸福感の大きさ。
-
s \in (0,1)
-
\delta \in (0,1)
つまり鈴木さんは「どんな魅力度をもった相手がいつ自分の元に告白してくるか」、「付き合っている相手と別れてしまう可能性」、 「自分が寿命を迎えてしまう確率」といった不確実性の中で暮らしていることとなります。そんな中鈴木さんは、自身の生涯における幸福度の期待値(以下期待生涯幸福度)を最大にするように意思決定を行います。つまり、鈴木さんの目的関数は以下のように表現できます。
\begin{aligned}
H_0 &= \max{\sum_{t=0}^{\infty}(1-\delta)^t\mathbb{E}[x_t]} \\
\mathrm{where}\ x_t &= \left\{
\begin{array}{ll}
\theta & \tiny{魅力度\ \theta\ の相手と付き合っている場合} \\
b & \tiny{誰とも付き合っていない場合}
\end{array}
\right.
\end{aligned}
分析(物語の本編)
最適な意思決定ルールを求める
さて先ほどまでの設定に基づいて、この鈴木さんの意思決定を分析していきましょう。
第 t 週に鈴木さんが生きているし、その時の期待生涯幸福度の最大値を V_{t} とします。この V_t の大きさは、「その時付き合っている恋人がいるかどうか」「付き合っている恋人の魅力度は何か」によって変わってしまいます。 そこで第 t 週時点で恋人がいない場合の幸福度の最大値を V_t(b), 魅力度 \theta の恋人と付き合っている場合の幸福度の最大値を V_t(\theta) と置くことにします。このとき、 V_t(b), V_t(\theta) はベルマン方程式を用いて再帰的に以下のように表現することができます:
\begin{aligned}
V_t(\theta) &= \theta + (1-\delta) \bigl[ s V_{t+1}(b) + (1 - s) V_{t+1}(\theta) \bigr] \\
V_t(b) &= b + (1 - \delta)\biggl[ \alpha \int_{\underline{\theta}}^{\bar{\theta}} \max\bigl\{V_{t+1}(\theta), V_{t+1}(b)\bigr\} f(\theta) d \theta + (1-\alpha)V_{t+1}(b) \biggr] \\
\end{aligned}
max オペレータの部分がまさに「告白してきた相手を受け入れるかどうか」を決定する意思決定の部分となっています。鈴木さんは魅力度 \theta の相手を受け入れることにより V(\theta) に移行することができ、拒否することにより V(b) の状況にとどまることができます。このどちらを選択する方が将来的に見て高い期待幸福度を得られるのか。それを見極めて意思決定をしていることになるのです。
このモデルでは時間 t それ自体に依存する変数が一つも存在しないため, 時間の添字をとって以下のように記述しなおすことができます。
\begin{aligned}
V(d) = b + (1 - \delta)\biggl[ \alpha \int_{\underline{\theta}}^{\bar{\theta}} \max\bigl\{V(\theta), V(b)\bigr\} f(\theta) d \theta + (1-\alpha)V(b) \biggr] \tag{1}
\end{aligned}
\begin{aligned}
V(\theta) &= \theta + (1-\delta) \bigl[ s V(b) + (1 - s) V(\theta) \bigr] \tag{2}
\end{aligned}
それぞれの式を変形することで以下を得ます。
\begin{aligned}
\delta V(b) = b + (1-\delta) \alpha \int_{\underline{\theta}}^{\bar{\theta}}\max\bigl\{ V(\theta) - V(b), 0 \bigr\}f(\theta)d\theta \tag{1-2}
\end{aligned}
\begin{aligned}
\delta V(\theta) = \theta - (1-\delta)s\bigl[ V(\theta) - V(b) \bigr] \tag{2-2}
\end{aligned}
ここで、b \in (\underline{\theta},\bar{\theta}) の仮定および V'(\theta)>0 であることから、ある \theta = \theta^* \in (\underline{\theta}, \bar{\theta}) が存在して, V( \theta ^* ) = V(b) となります。つまり「告白してきた相手を受け入れて付き合う状態に移行する価値」と、「受け入れず次の告白相手を待つ状態の価値」が同じになるような \theta^*」が存在することになります。この事実と V'(\theta)>0 の事実より以下のことが明らかになります。
さてここまで明らかになれば残された論点はその \theta^* を具体的に求めることです。 (1-2) を変形することで以下を得ます:
\begin{aligned}
\delta V(b) &= b + (1-\delta) \alpha \int_{\underline{\theta}}^{\bar{\theta}}\max\bigl\{ V(\theta) - V(b), 0 \bigr\}f(\theta)d\theta \\
&= b + (1-\delta) \alpha \biggl[ \int_{\underline{\theta}}^{\theta^*}0f(\theta)d\theta + \int_{\theta^*}^{\bar{\theta}} \bigl[ V(\theta) - V(b) \bigr] f(\theta)d\theta\biggr] \\
&= b + (1-\delta) \alpha \biggl[ \int_{\theta^*}^{\bar{\theta}} \bigl[ V(\theta) - V(b) \bigr] f(\theta)d\theta\biggr] \tag{1-3}
\end{aligned}
ここで (2-2) より
\begin{aligned}
&[\delta + (1-\delta)s]V(\theta) = \theta + (1-\delta)s V(b) \\
\Leftrightarrow\ & V(\theta) = \frac{\theta + (1-\delta)s V(b)}{\delta + (1-\delta)s}
\end{aligned}
この式の両辺から V(b) を引くと以下を得ることができます。
\begin{align}
V(\theta) - V(b) = \frac{\theta - \delta V(d)}{\delta + (1-\delta)s} \tag{2-3}
\end{align}
また (2-2) および V(\theta ^* ) = V(b) より \theta ^* = \delta V(\theta ^* ) = \delta V(b) が成立することが分かります。そのため (1-3) および (2-3) を以下のように変形できます。
\begin{aligned}
\theta^* &= b + (1-\delta) \alpha \biggl[ \int_{\theta^*}^{\bar{\theta}} \bigl[ V(\theta) - V(b) \bigr] f(\theta)d\theta\biggr] \tag{1-4}
\end{aligned}
\begin{aligned}
V(\theta) - V(b) &= \frac{\theta - \theta^*}{\delta + (1-\delta)s} \tag{2-4}
\end{aligned}
さらに (2-4) を (1-4) に代入して
\begin{align}
\theta^ * = b + \frac{(1-\delta)\alpha}{\delta + (1-\delta)s}\int_{\theta^* }^{\bar{\theta}}(\theta - \theta^*)f(\theta)d\theta \tag{E1}
\end{align}
ここで部分積分法を用いると以下の計算が成立することが分かります。
\begin{aligned}
\int_{\theta^* }^{\bar{\theta}}(\theta - \theta^*)f(\theta)d\theta &= \int_{\theta^* }^{\bar{\theta}}(\theta - \theta^*)F'(\theta)d\theta \\
&= \biggl[ (\theta - \theta ^* ) F(\theta) \biggr]_{\theta ^* }^{\bar{\theta}} - \int_{\theta^* }^{\bar{\theta}}F(\theta)d\theta \\
&= (\bar{\theta} - \theta^* ) \times 1 - \int_{\theta^* }^{\bar{\theta}}F(\theta)d\theta \\
&= \int_{\theta^* }^{\bar{\theta}}\bigl[ 1 - F(\theta) \bigr]d\theta
\end{aligned}
この結果を (E1) に適用すると以下を得ます。
\begin{align}
\theta^ * &= b + \frac{(1-\delta)\alpha}{\delta + (1-\delta)s}\int_{\theta^* }^{\bar{\theta}}\bigl[ 1 - F(\theta) \bigr]d\theta \\
&\equiv G(\theta^*) \tag{E2}
\end{align}
したがって鈴木さんの \theta^*、すなわち「告白を受け入れるかどうかのギリギリのライン」は G(\cdot) の不動点として求められることが分かります(表現が分かりづらい場合は「方程式の解として求められる」と読み替えて頂いてもここでは問題ございません)。したがって, G(\cdot) の関数型を以下で分析します。
\begin{aligned}
G(\underline{\theta}) &= b + \underbrace{\frac{(1-\delta)\alpha}{\delta + (1-\delta)s}\int_{\underline{\theta} }^{\bar{\theta}}\bigl[ 1 - F(\theta) \bigr]d\theta}_{>0} > b \\
\lim_{\theta^* \rightarrow \bar{\theta}}G( \theta^* ) &= b + \frac{(1-\delta)\alpha}{\delta + (1-\delta)s} \underbrace{\lim_{\theta^* \rightarrow \bar{\theta}}\int_{ \theta^* }^{\bar{\theta}}\bigl[ 1 - F(\theta) \bigr]d\theta}_{ \rightarrow 0 } = b \\
G'(\theta^* ) &= -\frac{(1-\delta)\alpha}{\delta + (1-\delta)s}[1-F(\theta^* )] <0 \ \ \mathrm{if}\ \ \theta^* \in (\underline{\theta},\bar{\theta}) \\
G''(\theta^* ) &= \frac{(1-\delta)\alpha}{\delta + (1-\delta)s}f(\theta^*) >0 \ \ \mathrm{if}\ \ \theta^* \in (\underline{\theta},\bar{\theta})
\end{aligned}
すなわちざっくり表現すると、\theta = \underline{\theta} の時点で b より大きい値を持つ、右肩下がりの関数であることが分かります。したがって (E2) : \theta^* = G(\theta^*) は図示すると以下のようになります。
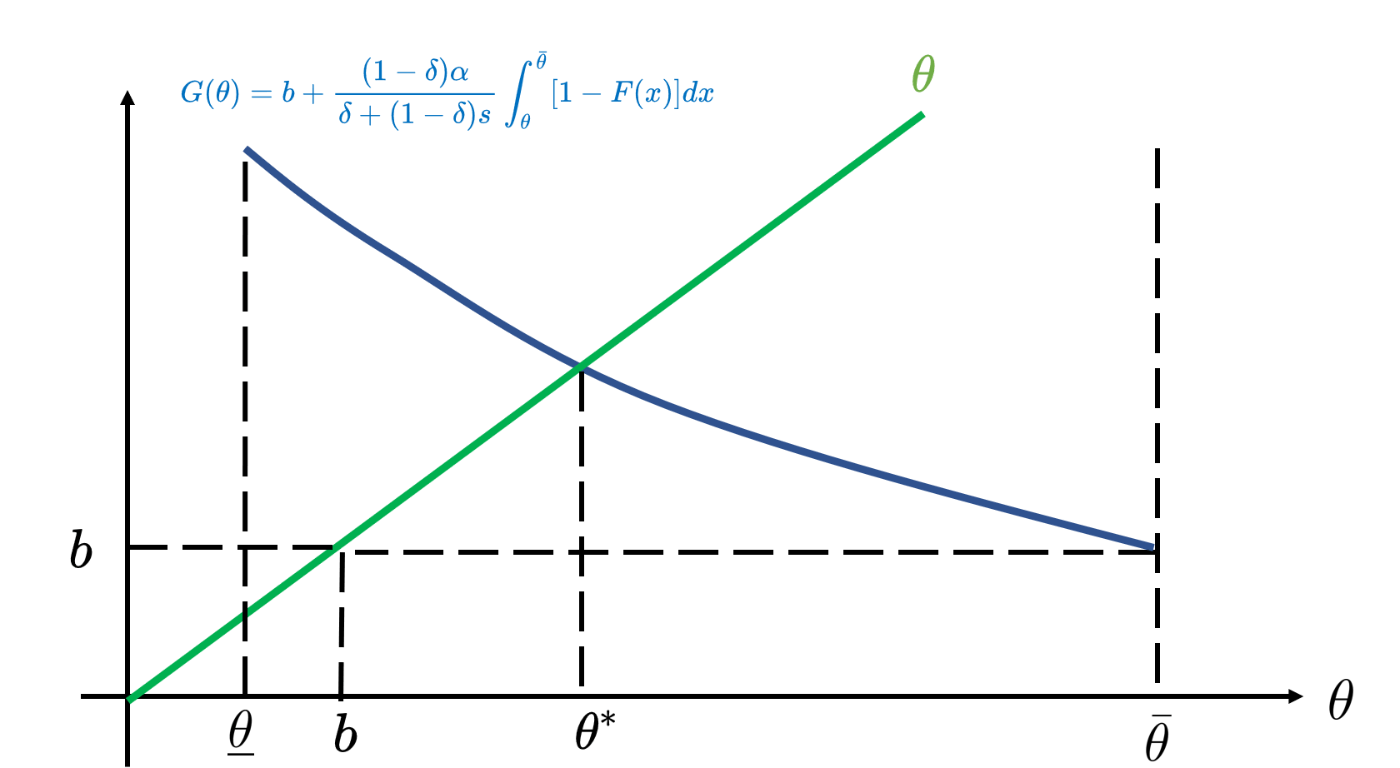
したがって鈴木さんの告白を受け入れるかどうかのギリギリのラインである \theta^* は方程式(元々は最適化問題)の解として一意に定まることが分かります。
パラメータの変化の影響を見る(比較静学分析)
さてここまで解いて合理的な鈴木さんの意思決定を方程式の解として表現することがせっかくできたのですから、色々とパラメータの変更が意思決定に与える影響を分析してみましょう。方程式の解を決める上で重要なのは G(\theta) の形状となる訳ですが、各パラメータの変動と G(\theta) の計上の間には以下の関係性が成立していることを容易に確かめることができます。
-
b が上昇すれば G(\theta) は上シフトします。
-
\delta が上昇すれば G(\theta) は下シフトします。
-
s が上昇すれば G(\theta) は下シフトします。
-
\alpha が上昇すれば G(\theta) は上シフトします。
また、図より G(\theta) が上に(下に)シフトすれば交点が右に(左に)にずれることが分かりますね。したがって「告白を受け入れるかどうかのギリギリのライン」は高く(低く)なります。この事実は以下のように解釈することができます。
-
b が高い場合、すなわち恋人がいなくても平気な場合は理想が高くなります。 別に告白してきた相手を受けれずともそれほど不満なわけでもなく、楽しむことができるため忍耐強く魅力度の高い相手との巡り合わせを待つことができるためです。
-
\delta が高い場合、すなわち将来よりも現在のことを重視する傾向が強い場合は理想が低くなります。 すごく理想的な方に告白されることを願って目の前の相手を振るよりも、現在幸福になることが相対的に優先されるためです.
-
s が高い場合、すなわち付き合っても別れる確率が高い場合は理想が低くなります。どうせすぐに別れてしまうのであれば、すごくいい人と付き合っても幸福度を得られる期間が短いためです。
-
\alpha が高い場合、 すなわちモテる場合は理想が高くなります。 目の前の相手を振ったとしても次に相手が現れるまでにそれほど期間を要しないため、良い相手に巡り合える確率が高いためです。
解析解の導出とシミュレーションの実施
今までは一般的な確率密度関数の形状を前提に議論してきましたが、よりイメージをわきやすくするために、分布の形状を 「下限0、上限1の一様分布」 に絞ってみましょう。この時、F(x) = x となるため、関数 G(\theta) の計上は以下のようになります。
G(\theta)= b + \frac{(1-\delta)\alpha}{\delta + (1-\delta)s}\int_{\theta^* }^{\bar{\theta}}\bigl[ 1 - x \bigr]dx
ここで元々の方程式である \theta = G(\theta) を解くと以下の解が得られます。
\begin{aligned}
\theta^* &= 1 + A^{-1} - \sqrt{A^{-1}[A^{-1} + 2(1-b)]} \\
\mathrm{where}\ \ A&\equiv \frac{(1-\delta)\alpha}{\delta + (1-\delta)s}
\end{aligned}
導出の過程が気になる方のために導出を以下ブロックにまとめておきました。これで解を求めることができましたので、パラメータにそれっぽい値を入れて計算結果を求めてみると楽しいです!実験に使えるソースコードをこちらに共有します。
方程式の解の導出過程
\begin{aligned}
\theta^* &= b + \underbrace{\frac{(1-\delta)\alpha}{\delta + (1-\delta)s}}_{A} \int_{\theta}^{1}(1-x)dx \\
&= b+ A*\biggl[x-\frac{x^2}{2}\biggr]_{\theta}^{1} \\
& = b + A*\biggl[ 1 \times (1-\frac{1}{2}) -\theta(1-\frac{\theta}{2}) \biggr] \\
\theta + A * \theta (1-\frac{\theta}{2}) &= b + A* 1/2 \\
\theta\biggl( 1 + A - \frac{A}{2}\theta \biggr) &= b + \frac{A}{2} \\
-\frac{A}{2}\theta^2 + (1+A)\theta - \biggl( b + \frac{A}{2}\biggr) &= 0 \\
\underbrace{\theta^2 - 2\frac{1+A}{A}\theta + \frac{2b + A}{A}}_{\tiny{A^{-1}\ を用いて変形}} &= 0 \\
\theta^2 - 2(1+A^{-1}) + 2bA^{-1}+1 &= 0\\
\theta^* &= 1+A^{-1} \pm \sqrt{(1+A^{-1})^2 - 2bA^{-1} -1} \\
& = 1 + A^{-1} \pm \sqrt{1+2A^{-1}+(A^{-1})^2 - 2bA^{-1} -1} \\
& = 1 + A^{-1} \underbrace{\pm \sqrt{A^{-1}(A^{-1}+2-2b)}}_{\tiny{\theta^*<1\ の条件より}} \\
& = 1 + A^{-1} - \sqrt{A^{-1}[A^{-1} + 2(1-b)]}
\end{aligned}
結論(物語のメッセージ)
この物語の主人公である、鈴木さんの「告白してきた相手を受け入れるかどうかの意思決定」は以下のルールに従います。
また、そのカットオフライン(理想の高さ)である \theta^* は鈴木さん自身のパラメータに依存して決まります。また、各パラメータと理想の高さには以下のような関係があり、その理由は以下です。
-
b が高い場合、すなわち恋人がいなくても平気な場合は理想が高くなります。 別に告白してきた相手を受けれずともそれほど不満なわけでもなく、楽しむことができるため忍耐強く魅力度の高い相手との巡り合わせを待つことができるためです。
-
\delta が高い場合、すなわち将来よりも現在のことを重視する傾向が強い場合は理想が低くなります。 すごく理想的な方に告白されることを願って目の前の相手を振るよりも、現在幸福になることが相対的に優先されるためです.
-
s が高い場合、すなわち付き合っても別れる確率が高い場合は理想が低くなります。どうせすぐに別れてしまうのであれば、すごくいい人と付き合っても幸福度を得られる期間が短いためです。
-
\alpha が高い場合、 すなわちモテる場合は理想が高くなります。 目の前の相手を振ったとしても次に相手が現れるまでにそれほど期間を要しないため、良い相手に巡り合える確率が高いためです。
また、魅力度の分布が下限0、上限1の一様分布に従うとしたときの理想の高さを求めるソースコードも用意しました。気になる方はこちらをご参照ください(上で提示したソースコードと同じです)。
最後まで見ていただき有難うございました!面白かったら「いいね」をいただけますと励みになります!
続編を書きました。ご関心あれば是非こちらもご覧下さい。
https://zenn.dev/joanofarc/articles/3c4465a4a118eb

Discussion