Zenn
Jij Tech BlogPublicationへの投稿
🐥

JijModeling-Transpiler-QuantumでQuantum Alternating Operator Ansatz

Kapiyva
2023/11/29に公開
Python
量子計算
jijmodeling
tech

JijModeling-Transpiler-Quantum(JTQ)は、数理最適化問題をqiskitやquri_partsのイジングハミルトニアンやQAOA[1]のansatzなどへ変換するためのライブラリーです。QAOAのような典型的なencodingの他に、Quantum Random Access Optimziation(QRAO)[2]なども一部サポートしています。

この記事では、Graph Coloring ProblemをQuantum Approximate Optimization AlgorithmとQuantum Alternating Operator Ansatz[3]を用いて解きながら、機能の説明をしたいと思います。

インストール

今回はqiskitを使ってシミュレーションを行なっていきたいと思います。
なので、次のようにJTQをpip installします。

pip install "jijmodeling-transpiler-quantum[qiskit]" --pre

インストールできたら、その他諸々の必要なライブラリーをimportしておきます。

from __future__ import annotations

import jijmodeling as jm
import jijmodeling_transpiler.core as jtc
import jijmodeling_transpiler_quantum.qiskit as jt_qk

from qiskit.primitives import Estimator, Sampler
from qiskit.algorithms.minimum_eigensolvers import QAOA
from qiskit.algorithms.optimizers import COBYLA
from qiskit import QuantumCircuit
import networkx as nx

import numpy as np
import matplotlib.pyplot as plt

数理モデルの実装

まずは、JijModelingでgraph coloring problemの数理モデルをを用いて実装していきます。

def graph_coloring_problem() -> jm.Problem:
    # define variables
    V = jm.Placeholder("V")
    E = jm.Placeholder("E", ndim=2)
    N = jm.Placeholder("N")
    x = jm.BinaryVar("x", shape=(V, N))
    n = jm.Element("i", belong_to=(0, N))
    v = jm.Element("v", belong_to=(0, V))
    e = jm.Element("e", belong_to=E)
    # set problem
    problem = jm.Problem("Graph Coloring")
    # set one-hot constraint that each vertex has only one color

    problem += jm.Constraint("one-color", x[v, :].sum() == 1, forall=v)
    # set objective function: minimize edges whose vertices connected by edges are the same color
    problem += jm.sum([n, e], x[e[0], n] * x[e[1], n])
    return problem

problem = graph_coloring_problem()
problem
\begin{array}{cccc}\text{Problem:} & \text{Graph Coloring} & & \\& & \min \quad \displaystyle \sum_{i = 0}^{N - 1} \sum_{e \in E} x_{e_{0}, i} \cdot x_{e_{1}, i} & \\\text{{s.t.}} & & & \\ & \text{one-color} & \displaystyle \sum_{\ast_{1} = 0}^{N - 1} x_{v, \ast_{1}} = 1 & \forall v \in \left\{0,\ldots,V - 1\right\} \\\text{{where}} & & & \\& x & 2\text{-dim binary variable}\\\end{array}

次に、問題のインスタンスを作成します。

G = nx.Graph()
G.add_nodes_from([0, 1, 2, 3, 4])
G.add_edges_from([(0, 1), (1, 2), (1, 3), (2, 3), (3, 4), (2, 4)])
nx.draw(G)

png

inst_E = [list(edge) for edge in G.edges]
color_num = 3
num_nodes = G.number_of_nodes()
instance_data = {"V": num_nodes, "N": color_num, "E": inst_E}
num_qubits = num_nodes * color_num

Quantum Approximate Optimazation Algorithm (QAOA)

ラフなQAOAの説明

Quantum Approximate Optimazation Algorithm (QAOA)は変分量子回路を用いた量子最適化アルゴリズムの一つです。詳細な説明は論文[1:1]を読んでいただくとして、ここでは大まかな概要だけを説明します。
QAOAでは、Ising Hamiltonian H_p= \sum_{ij}J_{ij}Z_iZ_jとX-mixer Hamiltonian H_m=\sum_iX_iを次のように作用させていくことで、変分量子回路を作ります。
初期状態を \ket{\psi_0}とすると,

\ket{\psi(\beta,\gamma)} = e^{-i\beta_pH_M}e^{-i\gamma_pH_P}\cdots e^{-i\beta_1H_M}e^{-i\gamma_1H_P}\ket{\psi_0}

と書くことができます。ここで\beta_k,\gamma_kは最適化すべきパラメータで、e^{-i\beta_kH_M}e^{-i\gamma_kH_P}という演算をp回繰り返すので、全部で2p個のパラメータが存在します。通常のQAOAでは、パラメータの総数はQubit数に依存せず、繰り返し回数のみに依存します。

\beta_k,\gamma_kの最適化は、次の1,2のステップを繰り返すことで行われます。

  1. H_Pの期待値\bra{\psi(\beta,\gamma)}H_P\ket{\psi(\beta,\gamma)}を量子デバイス上で計算する。
  2. 期待値が小さくなるようにパラメータを古典計算機で更新する。

この量子計算機上での期待値計算と古典計算機上でのパラメータの最適化を繰り返すことで、最小エネルギー\langle H_P \rangleとそれに対応する終状態を得ます。QAOAを数理最適化アルゴリズムとしてとらえると、この最小エネルギーが最小目的関数値に対応し、終状態が最適解になります。

JTQを用いたQAOAの実装

さて、Graph Coloring ProblemをQAOAで解いてみましょう。
QAOAを実行するためには、数理モデルをイジングハミルトニアンに落として、変分量子回路とハミルトニアンを量子計算用のライブラリで作ってとやらないといけないですが、
JTQを用いて簡単にイジングハミルトニアンを作成することができます。

まずは、JijModeling-Transpilerを用いて、JijModelingの数理モデルとインスタンスデータからCompiledInstanceを作成します。

compiled_instance = jtc.compile_model(problem, instance_data)

次に、JTQのtranspile_to_qaoa_ansatzを用いて、QAOAAnsatzBuilderを作成します。
このBuilderはどのように、イジングハミルトニアンを作るかの情報を受け取ります。ここでは、規格化は行わないようにし、制約条件はPenalty法で目的関数に加えるように設定しています[4]。

qaoa_builder = jt_qk.qaoa.transpile_to_qaoa_ansatz(compiled_instance,normalize=False,relax_method=jtc.pubo.RelaxationMethod.SquaredPenalty)

得られたBuilderのget_hamiltonianを用いることで、ハミルトニアンを作成することができます。
Penalty法における制約条件の重み係数multipliersを設定することができます。ここでは、とりあえず1としておきます。

hamiltonian, _ = qaoa_builder.get_hamiltonian(multipliers={"one-color": 1})

さて、ハミルトニアンができたので、実際にqiskitを使ってQAOAを実行してみましょう。
ここでは、qiskitのminimum_eigensolversにあるQAOAを用いてQAOAを実行してみたいと思います。

sampler = Sampler()
optimizer = COBYLA()
qaoa = QAOA(sampler, optimizer, reps=1)

compute_minimum_eigenvalueメソッドを用いることで、終状態のサンプリングまで行うことができます。

result = qaoa.compute_minimum_eigenvalue(hamiltonian)

result.eigenstateにはサンプリング結果が入っています。ここで、結果を見やすくするために、decode_from_quasi_distメソッドを用いて、結果をjm.SampleSetに変換します。
これを行うことで、解の形を数理モデルで定式化した形に自動で変換し、制約条件の破れや目的関数値なども計算してくれます。

sampleset = qaoa_builder.decode_from_quasi_dist(result.eigenstate)

最後にSamplingして得られた結果をプロットしてみます。

def plot_graph_coloring(graph: nx.Graph, sampleset: jm.SampleSet):
    # extract feasible solution
    feasibles = sampleset.feasible()
    if feasibles.evaluation.objective.size == 0:
        print("No feasible solution found ...")
    else:
        objectives = np.array(feasibles.evaluation.objective)
        lowest_index = np.argmin(objectives)

        # get indices of x = 1
        indices, _, _ = feasibles.record.solution["x"][lowest_index]
        # get vertices and colors
        sorted_vertices, sorted_colors = zip(
            *sorted(zip(*indices), key=lambda x: x[1])
        )
        # initialize vertex color list
        node_colors = [-1] * len(sorted_vertices)
        # set color list for visualization
        colorlist = ["gold", "violet", "limegreen", "darkorange"]
        # set vertex color list
        for i, j in zip(sorted_vertices, sorted_colors):
            node_colors[i] = colorlist[j]
        # make figure
        nx.draw_networkx(graph, node_color=node_colors, with_labels=True)
        plt.show()

plot_graph_coloring(G, sampleset)

png

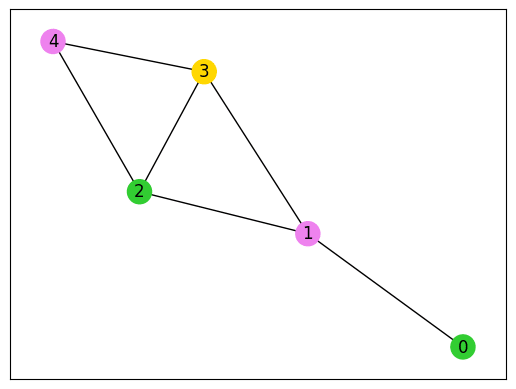
確かに、うまく色塗りができていることがわかりました。

Quantum Alternating Operator Ansatz

次に、Quantum Alternating Operator Ansatzを用いて、Graph Coloring Problemを解いてみます。
Quantum Alternating Operator Ansatzは、QAOAのmixer HamiltonianをX-mixerから問題に合わせたmixerに変更することで常に制約条件を満たした解のみを探索するように修正したものです。
詳細な話は元の論文[3:1]に渡すとして、ここではJTQでどのように実装するかをみてみます。

Graph Coloring problemの場合には、

\sum_k x_{v,k} = 1\quad \forall v

というonehot制約があります。
Graph Coloring problemに対するQuantum Alternating Operator Ansatzではonehot制約を満たすように、X-mixerからXY-mixerにしてしまいます。
ここでは、JTQを用いてこれを実装してみましょう。

まず、制約条件を抜いた数理モデルを用意します。

def graph_coloring_problem_wo_onehot() -> jm.Problem:
    # define variables
    V = jm.Placeholder("V")
    E = jm.Placeholder("E", ndim=2)
    N = jm.Placeholder("N")
    x = jm.BinaryVar("x", shape=(V, N))
    n = jm.Element("i", belong_to=(0, N))
    v = jm.Element("v", belong_to=(0, V))
    e = jm.Element("e", belong_to=E)
    # set problem
    problem = jm.Problem("Graph Coloring without Onehot")
    # set one-hot constraint that each vertex has only one color
    problem += jm.sum([n, e], x[e[0], n] * x[e[1], n])
    return problem

problem = graph_coloring_problem_wo_onehot()
problem
\begin{array}{cccc}\text{Problem:} & \text{Graph Coloring without Onehot} & & \\& & \min \quad \displaystyle \sum_{i = 0}^{N - 1} \sum_{e \in E} x_{e_{0}, i} \cdot x_{e_{1}, i} & \\\text{{where}} & & & \\& x & 2\text{-dim binary variable}\\\end{array}

先ほどと同様にハミルトニアンを作成します。

compiled_instance = jtc.compile_model(problem, instance_data)
qaoa_builder = jt_qk.qaoa.transpile_to_qaoa_ansatz(compiled_instance)
ising_operator, _ = qaoa_builder.get_hamiltonian()

次に、XY-mixerを作っていきます。XY-mixerは

XY_{ij} = \frac{1}{2}\left(X_iX_j + Y_iY_j \right)

と書くことができます。
これはbit i,jにある1と0を入れ替える演算子です。なので、onehot制約を満たすビット列100を別のonehot制約を満たすビット列010に変換することができます。

ここで、onehot制約がかかっているのは色に関する部分だけなので、数理モデルの表現でいえばx_{v0}とx_{v1}の間のビットを変換する必要があります。
一方で、通常これらの変数をqubitに埋め込むため、アルゴリズムを組み際にはどのビットがどの変数に対応しているかを覚えておき、適切に扱う必要があります。
JTQでは、変数の対応関係はCompiledInstanceの中のvar_mapに入っています。

var_map['variable_name'][indices]

という形で数理モデルの変数がどのqubitに対応したのかを確認することができます。
これを使って、XY-mixerを作ってみましょう。

ここで欲しいのはx_{v,k}とx_{v,k+1}の変換なので、compiled_instance.var_map.var_map["x"][(i,k)]のようにアクセスすることで対応するqubitのインデックスを得ることができます。

from qiskit.circuit import Parameter

def create_xy_mixer(beta:Parameter,num_nodes:int,num_color:int, compiled_instance: jtc.CompiledInstance):
    n = num_color*num_nodes
    qc = QuantumCircuit(n)
    var_map = compiled_instance.var_map.var_map["x"]
    #even
    for i in range(num_nodes):
        for k in range(0,num_color-1,2):
            qc.rxx(beta,var_map[(i,k)],var_map[(i,k+1)])
            qc.ryy(beta,var_map[(i,k)],var_map[(i,k+1)])
            
    #odd
    for i in range(num_nodes):
        for k in range(1,num_color-1,2):
            qc.rxx(beta,var_map[(i,k)],var_map[(i,k+1)])
            qc.ryy(beta,var_map[(i,k)],var_map[(i,k+1)])
            
    # ini-last
    if num_color % 2 == 1:
        for i in range(num_nodes):
            qc.rxx(beta,var_map[(i,0)],var_map[(i,num_color-1)])
            qc.ryy(beta,var_map[(i,0)],var_map[(i,num_color-1)])
    return qc

制約条件を守ような操作を行うので、初期状態も制約条件を満たすような状態からスタートする必要があります。
制約条件を満たす状態の重ね合わせ状態を作ってもいいですが、ここでは簡単のために明かにonehot制約を満たすような解として、全てのノードを同じ色で塗るという初期状態からスタートすることにします。

def create_initial_state(compiled_instance: jtc.CompiledInstance, num_nodes: int,num_color:int):
    n = num_color*num_nodes
    qc = QuantumCircuit(n)
    var_map = compiled_instance.var_map.var_map["x"]
    for i in range(num_nodes):
        qc.x(var_map[(i, 0)])
    return qc

以上でAnsatzが作成できたので、このAnsatzを用いて、実際に回してみたいと思います。
QAOAには、初期状態やmixerを選択する機能があるのでそれを用いて実行します。

sampler = Sampler()
optimizer = COBYLA()
initial_state = create_initial_state(compiled_instance, num_nodes,num_color=color_num)
xy_mixer = create_xy_mixer(Parameter("beta"), num_nodes, color_num, compiled_instance)
qaoa = QAOA(sampler, optimizer, reps=1,initial_state=initial_state,mixer=xy_mixer)

通常のQAOAの場合と同じように、得られたパラメータを用いて状態をサンプリングし、結果をプロットしてみましょう。

result = qaoa.compute_minimum_eigenvalue(ising_operator)
sampleset = qaoa_builder.decode_from_quasi_dist(result.eigenstate)
plot_graph_coloring(G, sampleset)

png

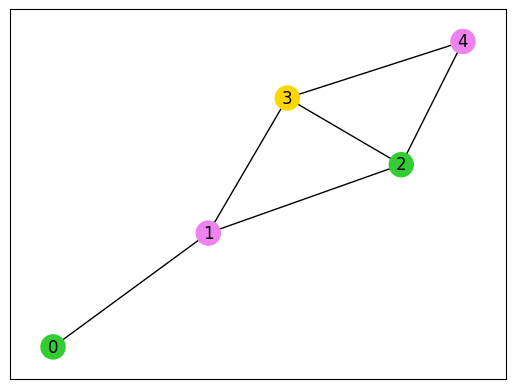
こちらの場合もうまく色分けできています。

まとめ

今回はJijModeling-Transpiler-Quantumを使って、QAOAとQuantum Alternating Operator Ansatzをやってみました。
JTQの中には、QRAOやminimal encodingといったQAOAに比べて少ない量子ビット数で問題をエンコードして最適化を行う手法もサポートしているので、今度はその辺りの機能についても説明してみたいです。
特に、QRAOはqiskitにも入っていない(3,2)-QRACとかもサポートしているので、(3,1)-QRACとかの比較とかも面白いかもしれないですね。

最後に

＼Rustエンジニア・数理最適化エンジニア募集中！／
株式会社Jijでは、数学や物理学のバックグラウンドを活かし、量子計算と数理最適化のフロンティアで活躍するRustエンジニア、数理最適化エンジニアを募集しています！
詳細は下記のリンクからご覧ください。皆さんのご応募をお待ちしております！
Rustエンジニア: https://open.talentio.com/r/1/c/j-ij.com/pages/51062
数理最適化エンジニア: https://open.talentio.com/r/1/c/j-ij.com/pages/75132

株式会社Jijではインターンを募集しています！
OpenJijやJijZeptの開発、アルゴリズム実装、企業課題のモデリング等、多彩なプロジェクトに触れる・挑戦する機会があります！

脚注

  1. A Quantum Approximate Optimization Algorithm ↩︎ ↩︎

  2. Approximate Solutions of Combinatorial Problems via Quantum Relaxations ↩︎

  3. From the Quantum Approximate Optimization Algorithm to a Quantum Alternating Operator Ansatz ↩︎ ↩︎

  4. JTQでは、Augmented Lagrangian methodもサポートしています。 ↩︎

GitHubで編集を提案
Jij Tech Blog
Jij Tech BlogPublication

Discussion