整数変数に対するSimulated Annealingについて②

この記事はJij Inc. Advent Calendar 2024の25日目の記事です。

概要

この記事は整数変数に対するSimulated Annealingについて①の続きです。
前回は二次制約無し多値最適化問題を念頭に擬似焼きなまし法(Simulated Annealing: SA)のアルゴリズムの概略を示しました。この記事では実際にアルゴリズムを実装して、最後にテスト計算を行ってみます。

遷移確率の計算について

この章では状態の遷移確率を効率的に計算する方法を説明します。SAの実装でおそらく一番大変なのがこの部分だと思われます^[1]。
この記事では状態の更新方法として、メトロポリス法、熱浴法、諏訪藤堂法を対象としています。これらの遷移確率は、状態の更新によるエネルギー差分$\Delta E$と温度$T$のみで定まります。したがって、エネルギー差分は事前に計算しておき、状態の更新があった場合^[2]にエネルギー差分も同時に更新する方法をとれば、遷移確率の計算は高速に行うことができそうです。
最後に遷移確率をエネルギー差分を使って書き直しておきましょう。簡単のため、現在の状態を$\bm{z}_{\lambda}$、候補状態を$\bm{z}_{\mu}$と表記します。また、現在の状態を含んだ候補状態の数を$n$とします。$\mu=1,2,\ldots,\lambda,\ldots,n$ということです。さらに、現在の状態と候補状態とのエネルギー差分を$\Delta E_{\mu}=E(\bm{z}_{\mu}) - E(\bm{z}_{\lambda})$と書きます。

メトロポリス法

まず、$\bm{z}_{\lambda}$除いた$n-1$個の候補状態からランダムに一つ選びます。それを$\bm{z}_{\mu}$とすれば、

$$p= \begin{cases} \exp(-\Delta E_{\mu}/T) & \text{if } \Delta E_{\mu} > 0, \\ 1 & \text{if } \Delta E_{\mu} \leq 0. \end{cases}$$

となります。

熱浴法

この式の分母分子を現在の状態のエネルギーで割ると以下を得ます。

$$p_{\mu}= \frac{\exp(-\Delta E_{\mu}/T)}{\sum^{n}_{\mu=1}\exp(-\Delta E_{\mu}/T)}$$

諏訪藤堂法

この式において、重み$w_{\mu}$をエネルギー差分を使った以下の式置き換えるだけです。

$$w_{\mu}=\exp(-\Delta E_{\mu}/T)$$

エネルギー差分の計算

まず初めに、初期状態が与えられた場合のエネルギー差分をどのように計算するか見ておきましょう。対象としている目的関数は以下のようなものでした。

$$E(\bm{z})=\sum_{i, j}J_{i,j}z_{i}z_{j} + \sum_{i} h_i z_{i},\quad L_i \leq z_{i} \leq U_i,\\ z_i\in\{L_i,L_i - 1,\ldots,U_i\}$$

ここで、目的関数の二次の項には$i=j$となる$J_{i,i}z^{2}_i$のような項もあることに注意してください。0または1を取るバイナリ変数$x$を考えている場合はこのような項は$x^2=x$となり一次の項になりますが、整数変数ではそうはなりません。
ある変数$z_m$を$z_m + a$に更新した場合、その前後でのエネルギー差分はどのように表現できるかを考えてみます。まずすぐに分かることとして、更新する変数$z_m$を含まない項はエネルギー差分には寄与しません。関係あるのは$z_m$を含む項です。そこで、変数$z_m$を含む項を抜き出すと以下のようになります。

$$F_m = \sum_{\substack{i\in S_m \\ i \neq m}} J_{i,m} z_i z_m + J_{m, m}z_m^2 + h_m z_m$$

ここで、$S_m$は変数$z_m$と相互作用で結ばれている変数のインデックスの集合です。$z_m$を$z_m + a$に更新すると$F_m$は以下のようになります^[3]。

$$F'_m = \sum_{\substack{i\in S_m \\ i \neq m}} J_{i,m} z_i (z_m + a) + J_{m, m}(z_m + a)^2 + h_m (z_m + a)$$

というわけで、変数の更新前後でのエネルギー差分$\Delta E = F'_m - F_m$は

$$\Delta E = a\left[\sum_{\substack{i\in S_m \\ i \neq m}} J_{i,m}z_i + h_m\right] + aJ_{m,m}(2z_m + a)$$

となります。この式にしたがって、エネルギー差分が計算できます。実装上は$\sum_{\substack{i\in S_m \\ i \neq m}} J_{i,m}z_i + h_m$という量をリストで保持しておくことにします。変数の値の差分$a$は実際に候補状態を生成して更新を試みる際に確定しますが、この量は$a$に依存していないため便利です。また、$aJ_{m,m}(2z_m + a)$という項は$a$に依存しており、$O(1)$で計算できるためリストで保持してもあまり利点がありません。

エネルギー差分の更新

さて、

$$\text{dE\_list[m]}=\sum_{\substack{i\in S_m \\ i \neq m}} J_{i,m}z_i + h_m$$

という、ある変数$z_m$の更新の際のエネルギー差分の一部の量を保持することにしたわけですが、実際に変数が更新されたら$\text{dE\_list[m]}$も更新しないといけません。これについて考えてみましょう。今、$z_{n}$が$z_{n} + b$に更新されたとします。このとき$z_{n}$を項として含む$\text{dE\_list[m]}$に関して更新が必要になります。$\text{dE\_list[m]}$は変数$z_m$と相互作用で結ばれている変数を項として含みますから、結局、更新対象は$z_{n}$と相互作用で結ばれている変数にかかわる$\text{dE\_list[m]}$ということになります。それは集合$S_{n}$に含まれるインデックスで指定される変数です。よって、初期化も含めると、以下のような擬似コードでかけることが分かります^[4]。

# dE_listの初期化
dE_list = [0]*N
for i in range(N):
    dE = h[i]
    for j in S[i]:
        dE += J[i, j]*z[j]
    dE_list[i] = dE


# 変数z_nがz_n + bに更新された場合のdE_listの更新
for i in S[n]:
    dE_list[i] += J[i,n]*b

書くまでもないかもしれませんが、この$\text{dE\_list}$を用いて変数$z_m$を$z_m + a$に更新した場合のエネルギー差分は以下のような関数で計算できます。

# mは更新を試みる変数のインデックス。ここではz_m。
# new_valueは更新後の変数の値。ここではz_m + a。
def get_dE(m, new_value):
    a = new_value - z[m]
    return a*(dE_list[m] + J[m, m]*(2*z[m] + a))

実装にあたって

これまで説明したことを用いて、実際に整数変数で構成された最適化問題に対するSAをpythonで実装してみました。ソースコードはここにあります。興味のある方や、実装に迷った際は参考にしてみてください^[5]。なお、注意点として、高速に動作するように意識して実装は行っていません。numpyをなどを利用して書き換えたり、その他の高速な数値計算に向いた言語^[6]で書き換えることで大幅に高速化すると思われます。
ここでは、実装にあたってエネルギー差分の更新以外で引っかかりそうなところや注意すべきところを列挙します。

初期温度と終温度

SAを行うにあたっては初期温度$T_{\text{max}}$と終温度$T_{\text{min}}$を決める必要があります。今回の実装では、変数$\bm{z}$の初期値に対応するエネルギー差分から決めました。具体的には
エネルギー差分の絶対値が最大のものを$\Delta E_{\text{max}}$、ゼロでない絶対値最小のものを$\Delta E_{\text{min}}$とすると、

$$T_{\text{min}}=\Delta E_{\text{max}}/\log(4),\\ T_{\text{max}}=\Delta E_{\text{min}}/\log(100)$$

となるように決めています。実装はここにあります。これはどういう「気持ち」かというと、$\Delta E_{\text{max}}$は大雑把には最も大きなエネルギー差分なので、そのような状態への遷移がアニーリングの初期段階ではだいたい25％くらい起きて欲しいなと思って$T_{\text{max}}$を決めています。一方で$\Delta E_{\text{min}}$は大雑把にはエネルギー差分が最も小さい変化と考えられるので、アニーリングの最後の方ではそのような状態への遷移がだいたい1％くらい起きても良いと考えて$T_{\text{min}}$を決めています。しかし、これはかなり適当に決めているので最適な値とは程遠いと考えられます^[7]。

オーバーフロー対策

熱浴法と諏訪藤堂法の遷移確率の計算では$\exp(-\Delta E/T)$を計算する必要がありますが、このとき$\Delta E$が負で大きいと$\exp(-\Delta E/T)$の計算でオーバーフローが起きてしまいます。これを避けるために実際の計算では最も小さい$\Delta E$の値を引いてあります。実際の実装における該当部分は熱浴法はここ、諏訪藤堂法はここになります。

諏訪藤堂法の遷移確率の計算の高速化

例えばこちらの論文によると、諏訪藤堂法の遷移確率の計算においてはWalker's alias method^[8]を用いることで遷移確率の計算を$O(1)$でできるようです。現在の実装では変数$z_m$が取りうる値が$n$個あるとすると、$O(n)$かかる実装になっています^[9]。

テスト計算

テスト計算と簡単なベンチマークを兼ねて、変数間にランダムな相互作用がある目的関数に対して、ここで実装したSAのアルゴリズムを適用してみました。
考えた目的関数としては以下のような単純なものになります。

$$E(\bm {z}) = \sum_{i, j} J_{i, j} z_i z_j$$

整数変数の取りうる値は$z_i\in \{-3, +3\}$とし、$J_{i, j}$は-1以上+1以下の一様乱数により生成しました。すべてのテスト計算においては同じ計算を乱数のseedを変えて100回実施しており、それらの標準偏差をエラーバーとしてつけています。

全結合模型

全結合模型、すなわち相互作用$J_{i, j}$がすべての$i, j$ペアに対してゼロでない模型に対してSAを実行しました。実験したnotebookはこちらにあります。
まずは、横軸をsweep数^[10]、縦軸を目的関数値、すなわちエネルギーとしたグラフは以下のとおりです。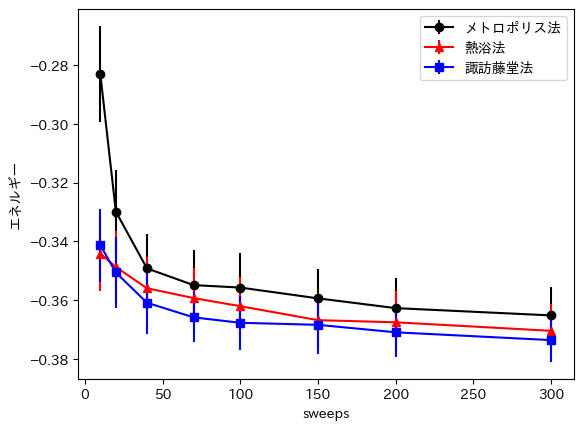

同じsweep数あたりで見ると、メトロポリス法より、熱浴法、諏訪藤堂法がより低いエネルギーに到達していることが分かります。エラーバーの範囲内ですが、わずかに諏訪藤堂法の方が熱浴法よりエネルギーが低い傾向も見て取れます^[11]。
次に横軸を計算時間にしたのが以下のグラフです。

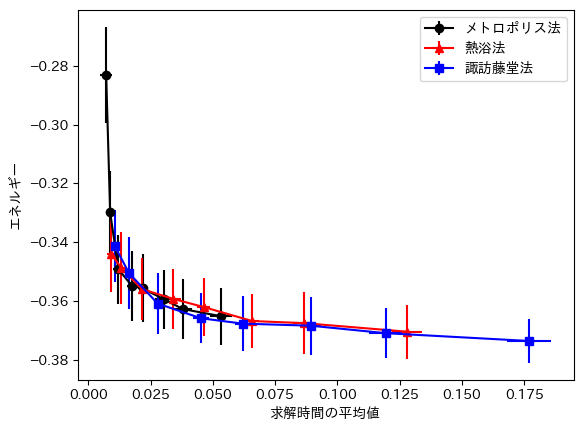
これを見ると、計算時間あたりでは、メトロポリス法、熱浴法、諏訪藤堂法いずれもほとんど同じエネルギー値となっています。現在の実装では熱浴法と諏訪藤堂法の遷移確率の計算に$O(n)$かかるため、$O(1)$で計算できるメトロポリス法に比べて不利です。おそらくこのことが原因で、sweepあたりではメトロポリス法に勝っていても時間あたりでは同程度になってしまうのでしょう。この部分は上でも触れた通り、アルゴリズムとしても、実装としても改善の余地があります。

疎結合模型

疎結合模型、すなわち相互作用$J_{i, j}$が特定の$i, j$ペアに対してゼロでなく、その他大部分の$i, j$ペアに対してはゼロという模型に対してSAを実行しました。実際にはおよそ10％の$J_{i, j}$がゼロでないような模型に対してテスト計算しています。実験したnotebookはこちらにあります。
まずは、横軸をsweep数^[10:1]、縦軸を目的関数値、すなわちエネルギーとしたグラフは以下のとおりです。

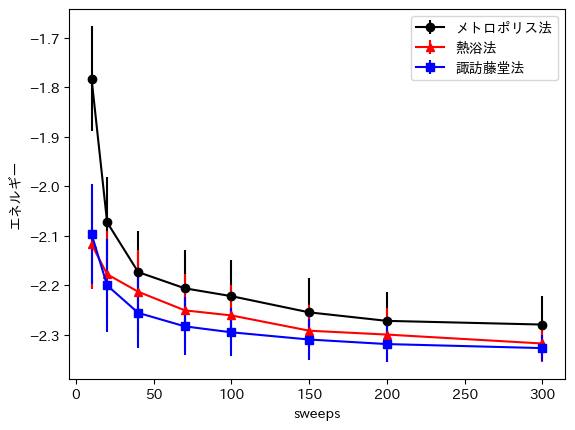
メトロポリス法より、熱浴法、諏訪藤堂法がより低いエネルギーに到達していますが、全結合模型の場合よりは差が小さいですね。
最後に横軸を計算時間にしたのが以下のグラフです。

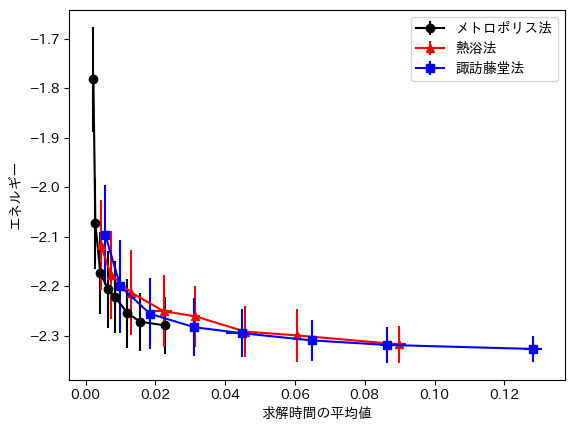
計算時間でみるとメトロポリス法が一番良いという結果になりました。もちろん解いているモデルによるところはありますが、やはり、諏訪藤堂法と熱浴法の遷移確率の計算については改善の余地がありそうです^[12]。

まとめ

今回と前回の記事では整数変数に対する疑似焼きなまし法を説明しました。また、実際に実装して簡単なテスト計算を行いました。当初考えていたほど熱浴法や諏訪藤堂法の性能が良くなかったので、ここはまだ改善の余地がありそうです。
次回のテーマとしては色々考えられますが、自分が現在興味を持っているのは、

• 遷移確率の計算にWalker's alias methodを導入して高速化する。
• 整数ナップサック問題のような、整数変数を含む最適化問題として多少なりとも意味のある問題を解く。
• 整数変数をバイナリエンコードしてQUBOにして解く場合との比較^[13]。
• 今回は整数変数の二次項までしか考慮していないが、これを高次の項を持つ目的関数を扱えるようにする^[14]。
• 実数変数を扱えるように拡張する^[15]。

あたりです。来年のアドベントカレンダーではここらへんの話題について書こうかなと思います。

募集してます！！！

Jijでは各ポジションを絶賛採用中です！
ご興味ございましたらカジュアル面談からでもぜひ！ご連絡お待ちしております。
数理最適化エンジニア（採用情報）
量子コンピューティングソフトウェアエンジニア（採用情報）
Rustエンジニア[アルゴリズムエンジニア]（採用情報）
研究チームPMO（採用情報）
オープンポジション等その他の採用情報はこちら

脚注

1. 前回の記事でも説明しましたが、ここで説明するような工夫をしない場合は動作が遅いですがSAの実装はとても簡単です。とはいえ、諏訪藤堂法は遷移確率の計算も多少大変ですが。。。

2. 当然ですが、状態の更新が行われなかった場合、エネルギー差分の更新をする必要はありません。何も変化していませんので。

3. 今は整数変数を考えているので$a$は当然整数ですが、以下の議論では$a$が実数でも成り立ちます。

4. pythonを意識した疑似コードですが、あくまで擬似コードなので、私が実際に実装したコードとは少し違います。でもデータの持ち方などが違うだけで、ロジックは同じです。

5. 一番大変なのがエネルギー差分の高速な計算だと言いましたが、ソルバーとして実装するためにはその他の細かいことを色々考える必要があり、こちらもそれなりに大変な作業です。

6. 筆者が知っているものとしてはFortran、C/C++、Rustあたりです。

7. そもそも、初期状態$\bm{z}$をランダムに決めているので、今の実装では乱数のseedを固定しない限り、初期温度と終温度が毎回変わるということになります。本来は相互作用だけから定まるはずなのでこれは少し変な感じがします。

8. こちらの解説が分かりやすいです。

9. 少なくとも二分探索を用いれば$O(\log(n))$にすることはできます。また、筆者はWalker's Alias Methodについて詳しく理解できていませんが、この手法はもしかしたら熱浴法にも使えるのかもしれません。

10. sweepについてはこちらに書いてあります。

11. 自分は専門家ではないですが、これは意外でした。諏訪藤堂法がもっと勝つと思っていたのですが、少なくともここで対象としているモデルではほとんど大差ないようです。一方で$S > 1/2$のイジング模型に対して、温度を固定して対応する物理量を計算する場合においては、諏訪藤堂法がメトロポリス法や熱浴法より収束が速いことは筆者も確認しています。今回は最適化アルゴリズムとしてのSAに諏訪藤堂法を用いてるので、ここらへんも関係するのかもしれません。

12. 終温度$T_{\text{min}}$が小さすぎるという可能性もあります。アニーリングの最後の方では、ほとんど最適解に近い状態が得られていると考えると、変数の更新はほとんど起きないと考えられます。もし$T_{\text{min}}$が小さすぎると、毎回遷移確率を計算して変数の更新を試みるけれど、更新は起きないということを繰り返すことになります。遷移確率の計算が$O(1)$でできるメトロポリス法に比べて、(今の実装では)$O(n)$かかる熱浴法と諏訪藤堂法はこの部分で計算量が明らかに違います。

13. 公開されている少なくないアニーリングソルバーが整数変数はバイナリエンコードしているので、実際上はここが最も興味あったりします。

14. 最適化問題としてそんなモデルが現れるのか疑問ですが、例えば$xy = z$のような非線形制約をペナルティ項として$(xy - z)^2$のように目的関数に埋め込むと４次の項が現れることになります。

15. メトロポリス法を用いるのであれば、候補状態をある連続な区間からランダムに選ぶように変更するだけで非常に簡単に実装できそうです。