jig.jp Engineers' BlogPublicationへの投稿
😎

「FFT一筆書きメーカー」というScratchプロジェクトを作ってみた話

jig.jp
に公開
FFT
Scratch
tech

はじめに

こんにちは！jig.jp Engineers' Blog Advent Calendar 2025の12月5日の記事を担当します たくと です！
今回は「FFT一筆書きメーカー」というScratchプロジェクトを作ってみた話を、ゆる〜く紹介します。

「FFT一筆書きメーカー」って何？って感じですよね。
ざっくり言うと「複数の単純な回転の組み合わせのアニメーションで、描いた一筆書きをなぞるように描き直すよ！」というやつです。

一番参考にしたサイトはモモヤマうさぎさんのブログです。
他には、AIへ聞いたり、Pythonを使ってデバッグしたり、YouTubeでマージソートの解説動画を見たりなどしながら作ってみました٩( 'ω' )و

↑ 今回作ったブロックたち

関連する内容

  • Scratch
    ブロックプログラミング言語だよ。
    MITが作っていて、8～16歳くらいが対象年齢として開発されているそうです。分かりやすくて誰でも楽しくプログラムが書けるのがとってもいいです( ˶'ᵕ'˶ )

Scratchの猫

  • オーダー表記
    N個のデータでどれくらい計算時間が増えるのかをざっくり表す記法です。オーダーや計算量と言われます。
    O(1)やO(N)、O(N^2)、O(N log(N))のようなものがあります。
    例えば、計算量O(N^2)ならNが5倍になったら計算にかかる時間は5^2=25倍になるって感じです。
    ただ、オーダー表記は厳密な速さではないので、同じO(N^2)の手法でも速度が違います。

  • 複素平面
    普通の(x, y)座標と少し違う表現方法で、例えば(12, 5)なら複素平面では12+5iみたいになります。

  • FFT
    時間のかかる離散フーリエ変換（O(N^2)）を高速（O(N log(N)）に行うための改良版の手法のことです。データ数はなんでもいいみたいですが、2^nの時が最も相性がいいし実装もシンプルになるみたいです。
    FFTには「周波数間引き型」と「時間間引き型」があって、途中の計算順とか並び替えタイミングが違います。
    今回は時間間引き型FFTでやりました！

  • バタフライ演算
    FFTで行われるメインの計算方法の名前です。見た目がちょっと複雑なので、🦋バタフライの名前がついてます。これ自体をFFTと呼ぶこともあります。

  • ビットリバース並び替え
    FFTで必要な並び替えです。ちょっと変わったシャッフルみたいなものです。バタフライ演算をしてFFTを行うと順番がぐちゃぐちゃな感じになるので、それを元に戻します。
    ビットリバースとある通り、2進数に変換した後にその順番を逆にした順番で並び替えるという方法です。

  • A, ω, φ（振幅/角速度/位相）に変換
    FFTで得られるのは複素数のリストなんですが、これでは扱いにくいです。そこで、振幅/角速度/位相にすることで扱いやすなります。リストの各要素がそれぞれ異なる回転を表しています。
    それぞれ、振幅と位相は|z|/Nとarg(z)で出すことができます。
    角速度は、リストの番号をkとすると、k番目の回転の角速度は(k<N/2)の間は2πk/N、それ以降は2π(N-k)/Nになります。（Scratchでは2πじゃなく360）

  • マージソート
    並んでいるものをきれいに大きさ順に並べ直す方法です。これも計算の速さは O(N log N)です！
    YouTubeのマージソート解説動画も役立ちました。
    単純なソートはO(N^2)のものがほとんどなのでFFTするよりも時間がかかってしまいます。笑
    それではせっかくのFFTの良さが台無しです。なので、今回は、データ数が2^nなので、マージソートを採用しました！

解説

今回作ったプロジェクトの主な処理の流れです。

  1. 入力のサイズ変更
    まずは入力サイズをスライダーで調整できます。書きたい一筆書きに合わせて調整してみてください。（7ぐらいがちょうどいいです）

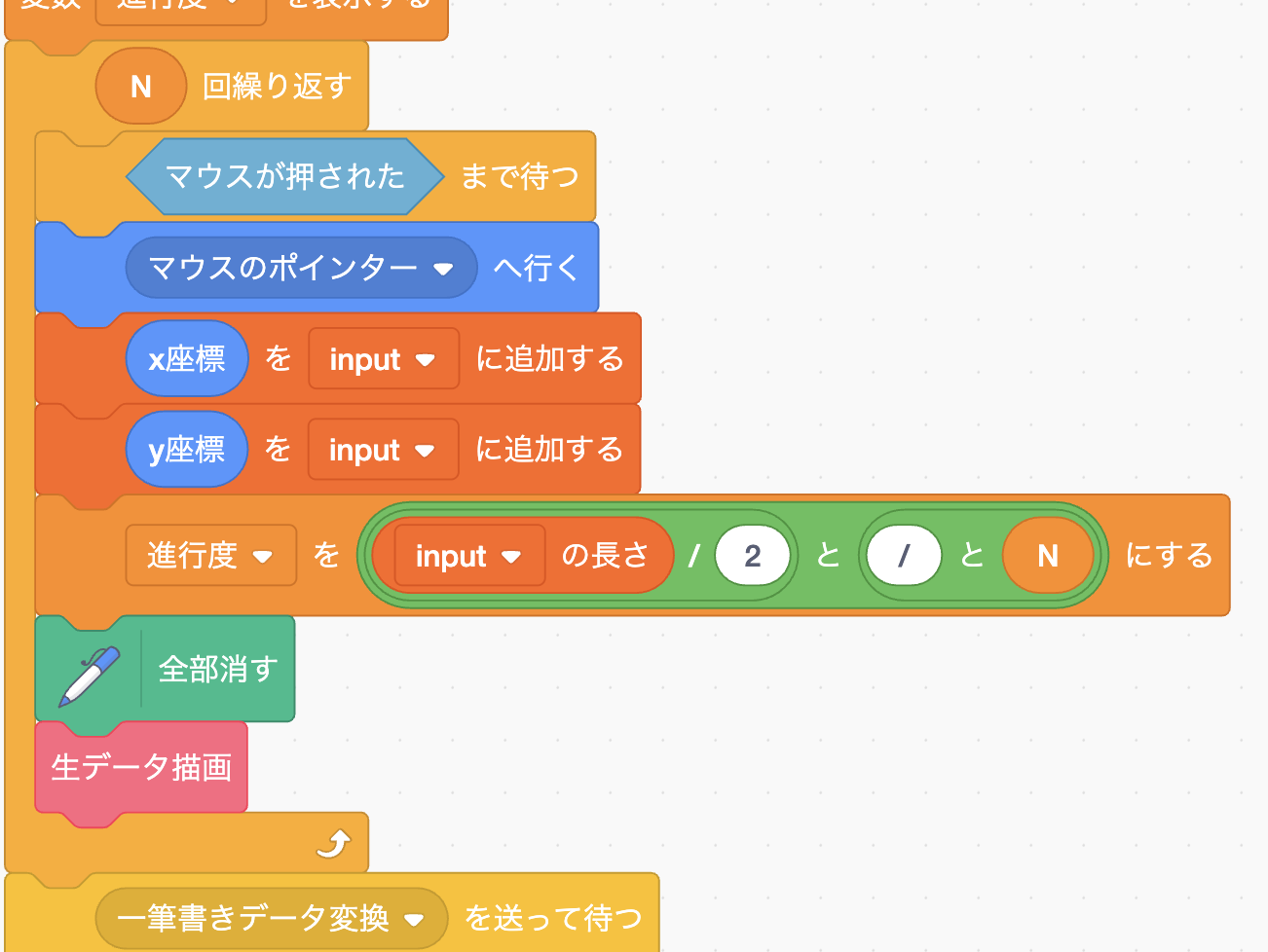
  2. 一筆書き入力
    画面をなぞると線が書けます。座標がFFTの入力データとして記録されます。
    進行度100%になるまでお絵描き！（100%で自動で次のステップに進みます）

  3. FFT（バタフライ演算）
    入力終わったらFFTでデータを分解します。でも、このままだと順番がおかしいので直す必要があります。

  4. ビットリバース並び替え
    FFTされたデータの並びをビットリバース順にして、直します。

  5. A, ω, φに変換
    それぞれの要素ごとで変換し、A, ω, φのリストを作ります。この段階で、もう一筆書きできる状態になっています。しかし、このままでは、振幅がバラバラで回転も途中から急に逆転するので、視覚的に微妙です。
    ここで、ポイント！
    Scratchは30fpsで時が流れるので、データをN個集めるのにN/30秒かかります。FFTでは角速度は360/Nが一番遅いやつなので、N秒で1周します。なので、角速度を30倍（つまり10800k/N）で計算しておくと元の速度と一致するようになります。

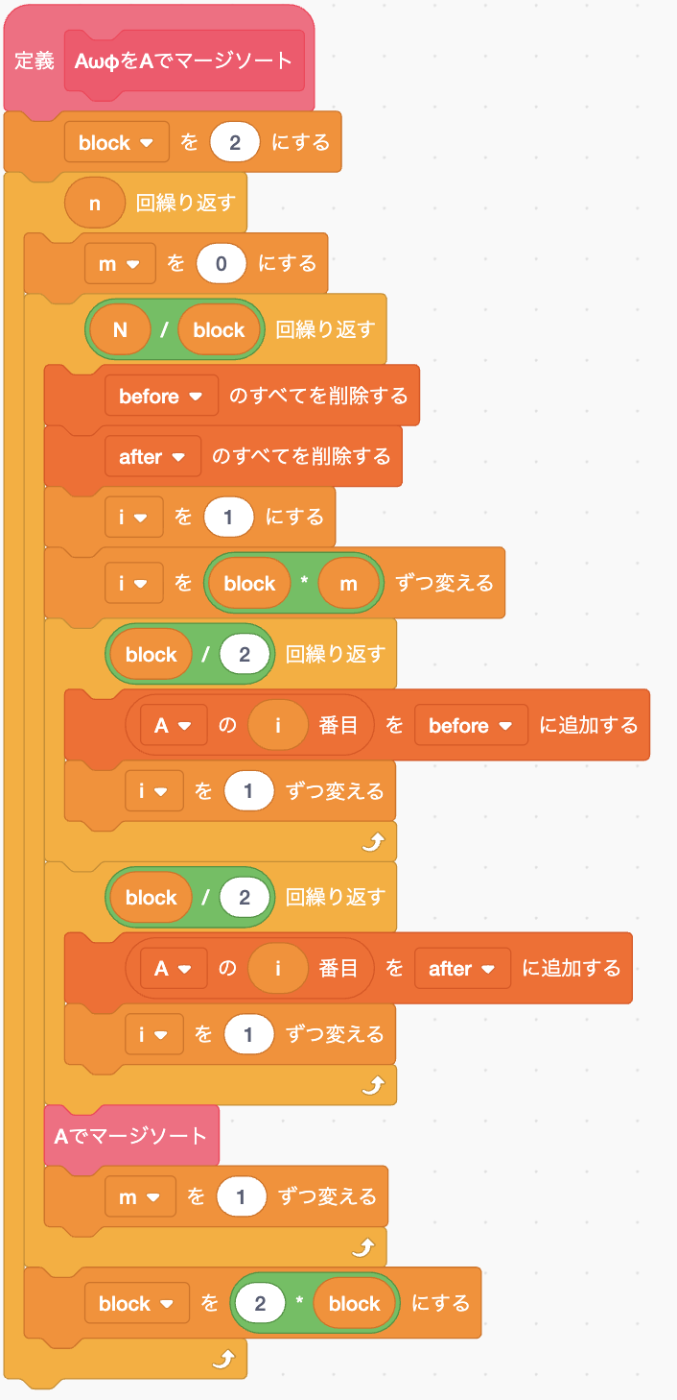
  6. Aの大きい順でソート
    変換したA, ω, φのリストをAの大きい順に並び替えます。振幅が大きいとその分大きく関与しているってことだからいい感じになります。

  7. 結果の描画アニメーション
    ソートされたA, ω, φをそのままScratchの「{90}度に向ける」ブロックと「{10}歩進む」ブロックでアニメーションで描画！描画を綺麗にしたかったのでちょっと長くなっちゃった
    Scratchでは90度が右＝時計回りが正なのが注意ポイント！

やってみた結果

一筆書きした形が振幅の大きい順でアニメーション表示されてよく見る感じのやつができました！

ScratchでFFTは前からやってみたかったので、できて嬉しいです。

FFTとマージソートのオーダーはどちらも O(N log N)なので、そこそこ大きくても軽いのもGoodですね！

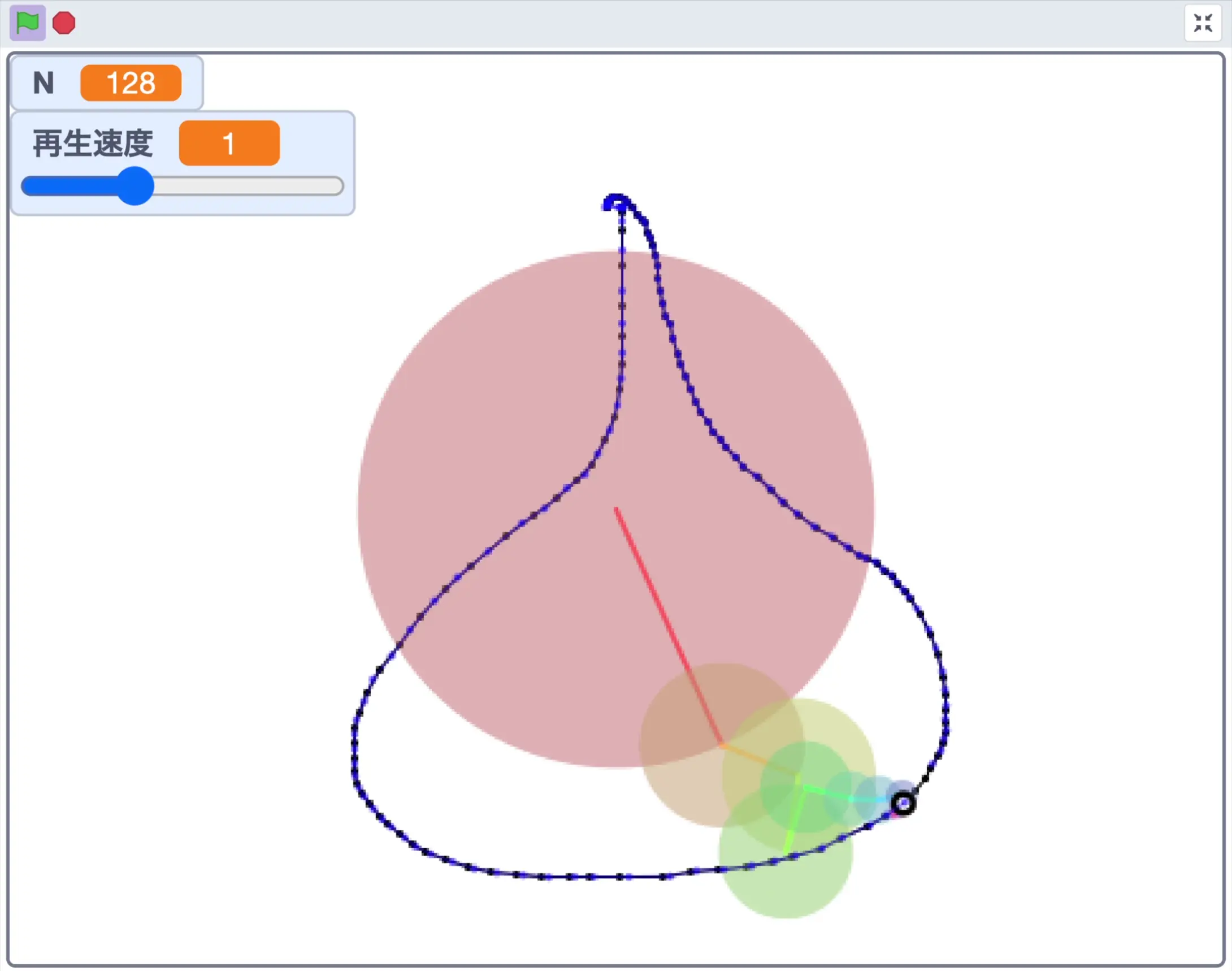
↑ 実際のアニメーションの様子

沼ったバグ

  • FFTのバタフライ演算で登場する W(N, i) という関数
    　これは、回転をN分割した内のi段階目の複素数を返す関数なんですが、回転の方向を反時計まわりで計算していて（本当は時計回り）全然見つけれませんでした！

  • Scratchの小数を指定したときの落とし穴
    　繰り返しブロックでは自動で四捨五入をしてくれるんですよ。でも、リストは切り下げだったというトラップ…！ 15.999999は15にされてしまいます....ここも罠でした（笑）

どちらも全然気づかなかったです。本当に気付けてよかった笑

まとめ

難しい理論はさておき、ScratchでFFTの面白さをきっちり感じられるプロジェクトになったと思います。
「一筆書きを円盤の組み合わせで再構成する」って、ちょっと魔法っぽくて楽しいです。

もし興味が湧いたら、FFT一筆書きメーカーを触ってみてください！

Scratchの未来はまだまだ明るいですね！

参考文献

jig.jp Engineers' Blog
jig.jp Engineers' BlogPublication

jig.jp のエンジニアたちがアプリ開発などの情報を発信するエンジニアブログです

Discussion