🏀

粒子フィルタをJulia言語で実装して状態空間モデルで遊ぶ

2021/11/23に公開

Julia

はじめに

この記事では『予測に活かす統計モデリングの基本』を読んで理解した~~つもりの~~一般的な粒子フィルタのロジックをJulia言語で実装しようとした成果を残すものです．
ついでに状態空間モデルを使って遊びました．

自分くらいのベイズ初心者に向けたつもりで書いてます．

粒子フィルタとは

粒子フィルタとは，以下のような確率的な状態空間モデルの潜在変数を推定するアルゴリズムの一種です．

\left\{ \, \begin{aligned} x_t &\sim p(x_t|x_{t-1}, \theta_{\mathrm{sys}}) \\ y_t &\sim p(y_t|x_t, \theta_{\mathrm{obs}}) \end{aligned} \right.

簡単に用語の説明をします．

潜在変数： $x_t$ のことです．観測データを裏で操る黒幕のような変数です．観測できないがモデルを仮定することで推測することが今回の目的です．
観測値： $y_t$ のことです．データとして得られるのはこの系列です．ここから裏の変数を予測したり，まだ得られていない先まで予測するのに使います．
$\theta_{\mathrm{sys}},\theta_{\mathrm{obs}}$ ：それぞれの確率モデルのハイパーパラメータ．今回はこれらは決め打ちで話を進めますがこれらをどう決めるかというモデル選択の話もあります．(以下では $\theta_{\mathrm{sys}},\theta_{\mathrm{obs}}$ は省略します．)

粒子フィルタの使える条件

粒子フィルタの使える条件は

$t\in \mathbb{Z}$
$p(x_t|x_{t-1})$ から $x_t$ が(簡単に)サンプリング可能
確率密度 $p(y_t|x_t)$ が(簡単に)計算可能

くらいのもので，適用範囲が異様なほどに広いです．
線形/非線形，連続/離散，・・・と幅広いモデルに対して使えそうです．

アルゴリズム

一般の粒子フィルタのアルゴリズムはとてもシンプルです．
1単位時間に3つのステップを踏むことを再帰的に行います．
なお，観測データ集合 $\{y_t\}_{t\in T\subset \mathbb{Z}}$ は所与のものとします．

Step0. 初期値の設定

初期時刻 $t=t_0$ と $N$ 個の潜在変数の初期値

\{x_{t_0}^{(n)}\}_{n \in [1,...,N]}

を定めます．粒子フィルタではこの潜在変数の集合の元を粒子と呼び，
粒子を更新していくことで潜在変数を推定していきます．

粒子の初期値は適当に1つずつ決めてもいいし，乱数で決めていってもいいし，
通常は全て同じ値で初期化することさえ問題ありません．
今回は全て同じ値で初期化することにします．

(今回はハイパーパラメータ $\theta_{\mathrm{sys}},\theta_{\mathrm{obs}}$ もこの段階で何らかの値に定めます．色んな値に変えて遊びましょう．)

Step1. 1期先予測

各粒子の1単位時間先の潜在変数をサンプリングします．

\forall n \,\,\,\, x_{t}^{(n)} \sim p\left(x_t^{(n)}|x^{(n)}_{t-1}\right)

このステップは各粒子ごとに独立なため，並列に実行することが可能です．

各粒子で同じ値のものがあったとしても，サンプリングが確率的に揺らぐようなモデルである限りは1期先の予測はバラバラな値に予測されます．
こういう事情から粒子が同じ値をもつことを許しても何の問題もないわけです．

Step2. 予測確率計算

所与の $y_t$ と先に得られた潜在変数の予測値 $x_t^{(n)}$ を観測モデルに代入することで予測確率を計算します．

\mu_t^{(n)} = p(y_t|x_t^{(n)})

各粒子の予測確率を計算したらこれらを正規化します．

\tilde{\mu}_t^{(n)} = \frac{\mu_t^{(n)}}{\sum_{n=1}^N\mu_t^{(n)}}

Step3. 粒子の更新

\forall n\,\,\,\,c_t^{(n)} \sim \mathrm{Categorical}(c_t^{(n)}|\tilde{\mu}_t)

x_t^{(n)} = c_t^{(n)\top} \begin{pmatrix} x_t^{(1)}\\ \vdots\\ x_t^{(N)}\\ \end{pmatrix}

$c_t^{(n)}\in\{0,1\}^N$ はある成分の値が1でそれ以外が0の値を持つ $N$ 次元のベクトルです．
$c_t^{(n)}$ はステップ2で計算した重み $\tilde{\mu}_t$ をパラメータとするカテゴリカル分布から生成します．
このステップによって実現確率の低い粒子は実現確率のより高い粒子に取って代わられる可能性が出てきます．極限的には最適な粒子が大多数を占めるようになっていく感じです．

$t\to t+1$ としてステップ1に戻ります．

Julia言語とは

https://julialang.org/

自分の理解では雑に書いてそこそこ早く動くスクリプト言語といった趣です．
個人的には組み込みで数理系のライブラリが充実しており可読性を損なわず短く書くことができるところが好きで推してます．

粒子フィルタの実装

using Random, Distributions
function ParticleFilter(data::AbstractArray{U, 1}, x₀::S, p, q, N::Integer) where {S, U}
    T = length(data)
    x = fill(x₀, N)
    X = fill(S[], T)
    for t in 1:T
        #Step 1: 1期先サンプリング
        X[t] = p.(x, t)
        #Step 2: 予測確率計算
        μ = q.(X[t], data[t], t)
        μ = μ / sum(μ) #Normalization
        #Step 3: 粒子の更新
        x = X[t][rand(Categorical(μ), N)]
    end
    return X
end

恐るべきことにライブラリのインポート宣言(using文)やコメント行を入れても16行しかない．．．
ブロードキャストで粒子の記述はとてもシンプルです．
また個人的には $\mu$ や $x_0$ のような記号を変数として使えるのも可読性の向上に寄与していて好きです．

Julia言語すごいなー．かっこいいなー．あこがれちゃうなー．

粒子フィルタの実装は終わってしまったので後はトイデータに対して具体的に状態空間モデルを作ってそのモデルを粒子フィルタで推定して遊んでいきます．

データ

データは『予測に活かす統計モデリングの基本』のサンプルデータを拝借しました．
プロットしてみると下図のような感じです．

モデル

書籍にも登場した非常にシンプルな線形状態空間モデルを採用します．

\left\{ \, \begin{aligned} x_t &\sim \mathrm{Normal}(x_{t-1}, \alpha^2\sigma^2) \\ y_t &\sim \mathrm{Normal}(x_t, \sigma^2) \end{aligned} \right.

このモデルを解釈すると，観測値 $y_t$ に対して真の値 $x_t$ があり我々はそれをノイズ付きで観測しているという状況で，真の値は今の期と次の期で値が大幅には変わりにくいという要請をしています． $x_t$ と $x_{t-1}$ が大幅に離れる確率は正規分布では急激に小さくなっていくからです．

一応この状態空間モデルが粒子フィルタで推定できるモデルかを確認すると

等間隔のデータなのでその間隔を1単位時間として定義すればよい！
正規分布からのサンプリングは簡単！
実現確率 $p$ は正規分布の確率密度から容易に計算することが可能！

p = \frac{1}{\sqrt{2\pi\sigma^2}}\exp{\left(-\frac{(y_t-x_t)^2}{2\sigma^2}\right)}

というわけで粒子フィルタによって潜在変数を推定することができそうです．

実装

モデルの実装と推定までのコードが以下です．

x₀ = data[1]
α = 0.1
σ = 0.5
num_particles = 100
p(x, t) = rand(Normal(x, α * σ))
q(x, y, t) = exp(-(y-x)^2/2σ^2)/√2π/σ
result = ParticleFilter(data[2:end], x₀, p, q, num_particles)
data_latent = [x₀; mean.(result)]

結果

推定された潜在変数をプロットしたものが下図になります．
推定値は粒子のアンサンブル平均を用いています．
小さな点は各時刻の粒子たちの値を表しています．

結果のプロット用コード

plot(data, label="observed data", title="Particle Filter (α=$α, σ=$σ, #particles=$num_particles)", xlabel="time", ylabel="value")
for n in 1:num_particles
    y = [r[n] for r in result]
    plot!([[]; y], label="",seriestype=:scatter, markersize=0.1)
end
plot!(data_latent, label="latent variable")

結果から，モデリングにおいて仮定したような滑らかな真の値が推定されているように見えます．
何となく合ってそうな空気感を醸しだしたところで次に欠損値のあるような観測値に対応できるように状態空間モデルを拡張しようと思います．
モデルを拡張することで精度を高めたり応用したりすることが可能=モデリング作業が無駄になりにくいのがベイズモデリングの強みの一つなので，まさに好例と思います．

応用：欠損値のあるデータ

データが完全な形でいつも得られるとは限りません．
例えばデータを計測する計器の経年劣化でたまにデータが取得できていないとか，
ウェブ上のアンケートでユーザが答えていない項目があるなどでデータは欠損します．

欠損値を含むデータは上で使ったデータに25%の確率で欠損値が挿入されるような形で人工的に生成しました．

欠損値のあるデータの生成用コード

data_missing = []
idx = 1
μ_true = 0.25
while idx ≤ length(data)
    if rand(Bernoulli(1-μ_true))
        push!(data_missing, data[idx])
        idx += 1
    else
        push!(data_missing, missing)
    end
end

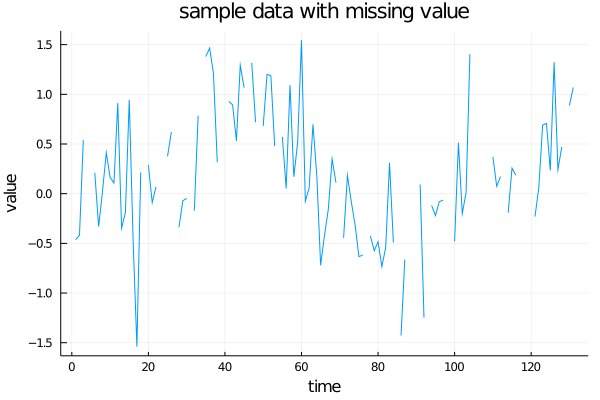
普通の機械学習では欠損箇所を補完するなどで対応することもあるようですが，ベイズモデリングの強みを活かして欠損しているという情報をも活用できるようなモデルを立てていきます．

モデル

潜在変数を今までの真の値 $x_t$ に加えて欠損パラメータ $\mu_t$ を追加します．
真の値と欠損パラメータは多変量正規分布でモデリングします．
欠損パラメータも真の値と同様なある種の”滑らかさ”を想定するという仮定です．
今回は真の値と欠損パラメータは無相関と仮定して共分散行列は対角行列でモデリングしています．
例えば真の値が大きいほど欠損値として観測されやすいなどの事前知識があれば非対角要素も含めてモデリングすることも考えられると思います．

\begin{pmatrix} x_t\\ \mu_t\\ \end{pmatrix} \sim \mathrm{Normal} \left( \begin{pmatrix} x_{t-1}\\ \mu_{t-1}\\ \end{pmatrix}, \sigma^2 \begin{pmatrix} \alpha^2, 0\\ 0, \beta^2\\ \end{pmatrix} \right)

欠損パラメータを元にデータが欠損しているかどうかを表す変数 $c_t$ をサンプリングします．
欠損パラメータは正規分布からサンプリングしているため負の値をとるため，ロジスティック関数を使って確率として解釈できる空間へ飛ばします．

c_t \sim \mathrm{Bernoulli}\left(\frac{1}{1+\exp{(-\mu_t)}}\right)

観測値 $y_t$ の取り得る値に $\phi_{\mathrm{missing}}$ を追加します．
i.e., $y_t\in\mathbb{R}\cup\{\phi_{\mathrm{missing}}\}$
$\phi_{\mathrm{missing}}$ は欠損値を表すシンボルで実数とは順序構造も代数構造も持たない記号と思ってください．Juliaのコード内では実数の他にmissingを値として取るようにしたことに対応しています．

y_t = \left\{ \, \begin{aligned} &\phi_{\mathrm{missing}}\,\,\,\, & \mathrm{if}\,\,\,\, c_t=1\\ &\sim\mathrm{Normal}(x_t, \sigma^2)\,\,\,\,&\mathrm{otherwise} \\ \end{aligned} \right.

先ほどと同様に粒子フィルタが利用できるか確認してみましょう．

先ほどと同様．
多変量正規分布のサンプリングは簡単！(今回は共分散行列が対角行列なので1次元正規分布を2回独立にサンプルするのと同じ)
欠損率を $\tilde{\mu}$ とすると欠損しない場合は正規分布の確率密度に $1-\tilde{\mu}$ を乗じるだけで計算可能！

というわけでやはり粒子フィルタによって推論可能なようです．

実装

モデルの実装と推定までのコードが以下です．

x₀ = data_missing[1]
α = 0.1
β = 0.1
σ = 0.5
num_particles = 100
p_missing(x, t) = rand(MvNormal(x, [α 0.0; 0.0 β]*σ))
function q_missing(X, y, t)
    x, μ = X
    p = 1/(1+exp(-μ))
    return ismissing(y) ? p : (1-p)*exp(-(y-x)^2/2σ^2)/√2π/σ
end
result = ParticleFilter(data_missing[2:end], [x₀, 0.5], p_missing, q_missing, num_particles)
data_latent_missing = [[r[n][1] for n in 1:num_particles] for r in result]
μ_missing = [[r[n][2] for n in 1:num_particles] for r in result];

結果

潜在変数の推定

潜在変数の推定結果は下図になります．

結果から分かる通り，データを弄ることなく自然に真の値として欠損箇所が推定されています．といっても今回はでたらめに欠損を挿入したので推定が合っているも何もないのですが・・・

結果のプロット用コード

plot(mean.(data_latent_missing), label="latent variable")
for n in 1:num_particles
    y = [r[n] for r in data_latent_missing]
    plot!([[]; y], label="",seriestype=:scatter, markersize=0.01)
end
plot!(data_missing, label="observed data", title="Particle Filter (α=$α, β=$β, σ=$σ, #particles=$num_particles)", xlabel="time", ylabel="value")

欠損確率の推定

また，欠損パラメータを推定しているのでそこから欠損確率も推定できます．
欠損確率の推定結果は下図になります．

正解は25%で一定なのですが，サンプル数が不足していたのか結果はかなりぶれているように見えます．

結果のプロット用コード

hline([μ_true], label="μ_true=$μ_true")
for n in 1:num_particles
    y = [r[n] for r in μ_missing]
    y = 1 ./ (1 .+ exp.(-y))
    plot!([[]; y], label="",seriestype=:scatter, markersize=0.01)
end
plot!(1 ./(1 .+ exp.(-mean.(μ_missing))), label="predict", title="Prob. missing", xlabel="time", ylabel="probability")

まとめ

~~粒子フィルタ完全に理解した~~
Julia言語で十数行で実装できた(たぶん)
サンプルデータを簡単な状態空間モデルで推定してみた
状態空間モデルを拡張して欠損のあるデータも推定してみた

今回作って遊んだ状態空間モデルをさらに拡張したいとなれば方向性は色々あると思いますが，例えば

潜在変数の精緻化：周期性の要素やイベント性の要素などの知識を活用してモデルの説明力，予測力を高めていくなど(書籍の方向性)
欠損推定の精緻化：周期的に欠損しているとか潜在変数の値に連動して欠損確率が変動するなどの知見をデータから得たならばこれをモデルに取り入れることで欠損するかどうか自体を予測してみるなど
粒子フィルタの並列化：~~並列化よくわからんので~~今回は簡単のため並列化を行いませんでしたが，並列化を施せばより多粒子で高精度な推定が可能になるかもしれません．
ハイパーパラメータ最適化(モデル選択)：ハイパーパラメータをデータから決定することも可能です．ハイパーパラメータの事前分布を用意する，経験ベイズ，最尤推定，ガウス過程回帰など

があると思います．是非遊んでみてください．

理論やコードのアドバイス，コメントなどお待ちしております！

References

『予測にいかす統計モデリングの基本』

この記事を書くきっかけとなった本でとても分かりやすいです．ベイズモデリング初心者の方におすすめです．
粒子フィルタの概念図は特に白眉といって良く，この記事のコードは実質その1枚絵からひねり出されています．

データに欠損がある場合の教師あり学習

ベイズ推論でおなじみ須山さんのブログ記事になります．
本記事では観測データが1次元のものを扱いましたが，この記事では入力と出力の組を観測データとして扱い，入力に欠損がある場合について取り扱っています．
他の記事もとてもわかりやすく一読をおすすめします．

はじめに

粒子フィルタとは

粒子フィルタの使える条件

アルゴリズム

Step0. 初期値の設定

Step1. 1期先予測

Step2. 予測確率計算

Step3. 粒子の更新

Julia言語とは

粒子フィルタの実装

データ

モデル

実装

結果

応用：欠損値のあるデータ

モデル

実装

結果

潜在変数の推定

欠損確率の推定

まとめ

References

Discussion