1. マシューズ相関係数
マシューズ相関係数(Matthews Correlation Coefficient)は、機械学習における二値分類タスクの評価指標の一つです。観測値と同じく、予測値が二値である場合に用います。
0と1の割合が大きく偏った不均衡データに対して、正解率(Accuracy)で予測性能を測るのは適切でない、というのはよく知られている事実です。
一方、不均衡データにも用いられる評価指標であるF1-scoreについても、1が多数を占めるようなデータ(普通はそのようにラベル付けしませんが)に対しては、問題が生じる可能性があります。具体的には、常に1を返すモデルのF1-scoreが高くなってしまいます。
そのような問題を生じない評価指標として、マシューズ相関係数が挙げられます。
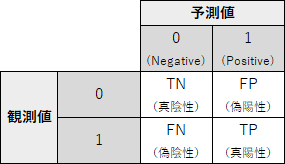
これは、混同行列の要素を用いて以下のように定義されます。
\mathrm{MCC} =
\frac{TP \times TN - FP \times FN}{\sqrt{(TP+FP)(TP+FN)(TN+FP)(TN+FN)}}
マシューズ相関係数は-1から1の範囲の値を取り、予測値と観測値が完全に一致する場合に1となるため、大きいほど予測モデルの性能がよいとみなせます。
統計学において、二値変数同士の相関を測る指標として、四分点相関係数あるいは\phi係数と呼ばれるものがありますが、それを混同行列に適用したものはマシューズ相関係数と同じです。
上式の定義は直感的に理解しにくいですが、何の事は無い、単に予測値と観測値の(ピアソンの積率)相関係数を取ると、マシューズ相関係数に一致します。
その事実に言及している記事はインターネット上にも見られますが、計算過程まで示しているものは簡単に見付からなかったので、本記事で記述します。
余談ですが、不均衡データに用いる評価指標としては、よりシンプルな以下のBalanced Accuracyもあります。
\text{Balanced Accuracy} = \frac{1}{2} \left( \frac{TP}{TP+FN} + \frac{TN}{TN+FP} \right)
2. 一致を示す計算過程
まず、2変数(x, y)のデータ列があったとき、x, yのピアソンの積率相関係数は以下のように定義されます。
r_{xy} = \frac
{\sum_{i=1}^{n} (x_i - \bar{x})(y_i - \bar{y})}
{\sqrt{\sum_{i=1}^{n} (x_i - \bar{x})^2} \sqrt{\sum_{i=1}^{n} (y_i - \bar{y})^2}}
これを予測値\hat{y}と観測値yについて計算したr_{\hat{y}y}が、マシューズ相関係数に一致することを示します。
(1) 分母の左部分に相当する\sqrt{\sum_{i=1}^{n} (\hat{y}_i - \bar{\hat{y}})^2}
(2) 分母の右部分に相当する\sqrt{\sum_{i=1}^{n} (y_i - \bar{y})^2}
(3) 分子に相当する\sum_{i=1}^{n} (\hat{y}_i - \bar{\hat{y}})(y_i - \bar{y})
のそれぞれについて、混同行列の要素を使って地道に計算するだけです。
- (1) \sqrt{\sum_{i=1}^{n} (\hat{y}_i - \bar{\hat{y}})^2}
\hat{y}_iが1であるものの数は(TP+FP)、0であるものの数は(TN+FN)ですから、以下のように計算できます。
\sqrt{\sum_{i=1}^{n} (\hat{y}_i - \bar{\hat{y}})^2}
= \sqrt{(TP+FP)(1 - \bar{\hat{y}})^2 + (TN+FN)(0 - \bar{\hat{y}})^2}
そして、\bar{\hat{y}} = \frac{TP+FP}{TP+TN+FP+FN}と表せるので、これを代入すると、
\begin{aligned}
\sqrt{\sum_{i=1}^{n} (\hat{y}_i - \bar{\hat{y}})^2}
&= \sqrt{
(TP+FP)\left(1 - \frac{TP+FP}{TP+TN+FP+FN}\right)^2 +
(TN+FN)\left(0 - \frac{TP+FP}{TP+TN+FP+FN}\right)^2
} \\
&= \sqrt{
\frac{(TP+FP)(TN+FN)^2}{(TP+TN+FP+FN)^2} +
\frac{(TN+FN)(TP+FP)^2}{(TP+TN+FP+FN)^2}
} \\
&= \sqrt{\frac{(TP+FP)(TN+FN)}{TP+TN+FP+FN}}
\end{aligned}
となります。
- (2) \sqrt{\sum_{i=1}^{n} (y_i - \bar{y})^2}
y_iが1であるものの数は(TP+FN)、0であるものの数は(TN+FP)ですから、以下のように計算できます。
\sqrt{\sum_{i=1}^{n} (y_i - \bar{y})^2}
= \sqrt{ (TP+FN)(1 - \bar{y})^2 + (TN+FP)(0 - \bar{y})^2}
そして、\bar{y} = \frac{TP+FN}{TP+TN+FP+FN}と表せるので、これを代入すると、
\begin{aligned}
\sqrt{\sum_{i=1}^{n} (y_i - \bar{y})^2}
&= \sqrt{(TP+FN)(1 - \frac{TP+FN}{TP+TN+FP+FN})^2 + (TN+FP)(0 - \frac{TP+FN}{TP+TN+FP+FN})^2} \\
&= \sqrt{\frac{(TP+FN)(TN+FP)^2}{(TP+TN+FP+FN)^2} + \frac{(TN+FP)(TP+FN)^2}{(TP+TN+FP+FN)^2}} \\
&= \sqrt{\frac{(TP+FN)(TN+FP)}{TP+TN+FP+FN}}
\end{aligned}
となります。
(1)と(2)の結果から、r_{\hat{y}y}の分母は、
\frac{\sqrt{(TP+FP)(TP+FN)(TN+FP)(TN+FN)}}{TP+TN+FP+FN}
となります。マシューズ相関係数の片鱗が見えますね。
- (3) \sum_{i=1}^{n} (\hat{y}_i - \bar{\hat{y}})(y_i - \bar{y})
以下のように、混同行列の各要素に関して和を計算すると、
\begin{aligned}
\sum_{i=1}^{n} (\hat{y}_i - \bar{\hat{y}})(y_i - \bar{y})
&= TN \left(0 - \bar{\hat{y}} \right) \left(0 - \bar{y} \right)
+ FP \left(1 - \bar{\hat{y}} \right) \left(0 - \bar{y} \right)
+ FN \left(0 - \bar{\hat{y}} \right) \left(1 - \bar{y} \right)
+ TP \left(1 - \bar{\hat{y}} \right) \left(1 - \bar{y} \right) \\
&= \frac
{TN(TP+FP)(TP+FN) - FP(TN+FN)(TP+FN) - FN(TP+FP)(TN+FP) + TP(TN+FN)(TN+FP)}
{(TP+TN+FP+FN)^2} \\
&= \frac
{(TP \times TN - FP \times FN)(TP+FN) + (TP \times TN - FP \times FN)(TN+FP)}
{(TP+TN+FP+FN)^2} \\
&= \frac{TP \times TN - FP \times FN}{TP+TN+FP+FN}
\end{aligned}
となります。
(1)(2)(3)を合わせると、
r_{\hat{y}y}
= \frac{TP \times TN - FP \times FN}{\sqrt{(TP+FP)(TP+FN)(TN+FP)(TN+FN)}}
となり、マシューズ相関係数の定義に一致することが示せました。
以上です。
Discussion