イグノーベル賞2022経済学賞の論文「Talent vs Luck: the role of randomness in success and failure」を読む
なぜ成功は、もっとも才能のある人ではなく、もっとも幸運な人に行くかの数学的な説明
個人的まとめ
- 才能(IQ)の分布は正規分布だが、成功の代名詞とされる富の分布はべき分布に従う → 才能と成功は相関がないのではないか?という仮説
- 結局、成功はランダム的な「幸運イベント」に依存し「(一番多い)平凡で、かつ幸運な人」が成功する
- 成功の確率を高めるための最善の戦略は、個人の活動、アイデアの生産、他者とのコミュニケーションを広げ、多様性と相互理解を求めること
- オープンマインドな人間であること、他者と接する準備ができていることが、幸運な出来事(個人の才能を生かすこと)に遭遇する確率を最も高くするのである。
Abstract
競争の激しい欧米文化で主に支配的な実力主義のパラダイムは、成功は主に才能、知性、スキル、賢さ、努力、意志、ハードワーク、リスクテイクなどの個人の資質によるという信念に根ざしている。時には、物質的に大きな成功を収めるためには、ある程度の運が必要であることを認めることもあります。しかし、実のところ、個人の成功物語において、外的な力の重要性を過小評価することは、むしろよくあることなのです。知能(あるいは、より一般的には才能や個人的資質)は人口の間でガウス分布を示していることは非常によく知られているが、一方、成功の代名詞とされる富の分布は典型的にはべき乗則(パレート則)に従っており、大多数の貧しい人々とごく少数の億万長者が存在する。このような、典型的なスケール(平均的な才能や知能)を持つ入力の正規分布と、スケールによらない出力分布との間の不一致は、何らかの隠れた成分が背後に働いていることを示唆している。この論文では、非常に単純なエージェントベースのおもちゃのモデルを用いて、そのような成分が単なるランダムネスであることを示唆する。特に、人生で成功するためにはある程度の才能が必要であることが事実である場合、最も才能のある人が成功の頂点に立つことはほとんどなく、平凡だが感覚的に幸運な人に追い越されてしまうことを示す。私たちの知る限り、膨大な文献の行間に暗黙のうちに示唆されていたこの直感に反する結果が、ここで初めて定量化された。この結果は、到達した成功のレベルに基づいて功績を評価することの有効性に新たな光を当てるとともに、結局のところ他の人より単に運が良かっただけの人に過剰な栄誉や資源を配分することの危険性を強調するものである。また、このモデルの助けを借りて、いくつかの政策仮説を取り上げ、比較することで、能力主義、多様性、イノベーションを向上させるための、公的研究資金の最も効率的な戦略を示すことができる。
www.DeepL.com/Translator(無料版)で翻訳しました。
4. Conclusive remarks (結論) (先に持ってきています)
この論文では、いくつかの非常に単純で合理的な仮定から出発して、人々のキャリアの成功における才能と運の役割を定量化することができるエージェントベースモデルを提示した。シミュレーションの結果、才能はエージェント間でガウス分布を持つが、結果として40年の労働人生の後の成功/資本の分布は、実世界で見られる富の分布の「80-20」パレートの法則を尊重したべき乗則に従うことが示された。シミュレーションの重要な結果は、最も成功したエージェントは、最も才能のある人ではなく、ガウス型才能分布の平均に近い人であるということであり、これも文献でしばしば報告される定型的な事実である。このモデルは、個人の成功の最終的なレベルを決定する上で、しばしば過小評価される幸運な出来事の重要性を示している。報酬や資源は通常、すでに高いレベルの成功に到達した者に与えられるため、誤って能力・才能の尺度として考えられているが、この結果はさらに有害な阻害要因となり、最も才能ある者に機会の欠如をもたらす。我々の結果は、我々が「素朴な実力主義」と呼ぶパラダイムの危険性を浮き彫りにした。このパラダイムは、成功の決定要因のうちランダム性の役割を過小評価しているため、最も有能な人々に栄誉と報酬を与えることができないのである。この点で、いくつかの異なるシナリオを調査し、より効率的な戦略を検討した。この戦略では、運の予測不可能な役割を相殺し、真の能力主義の主目的であるべき、最も有能な人々に多くの機会と資源を与えることができる。このような戦略は、社会全体にとっても最も有益であることが示されている。なぜなら、研究におけるアイデアや視点の多様性を高め、イノベーションを促進する傾向があるからである。
1. Introduction
多くの物理的、生物学的、社会経済的な複雑系における冪乗則分布の偏在は、それらの強く相関した動的挙動とスケール不変な位相構造の一種の数学的サインとして見ることができる [1, 2, 3, 4]。社会経済的な文脈では、パレートの研究 [5, 6, 7, 8, 9] 以降、富の分布がべき乗則に従うことがよく知られており、その典型的なロングテールの形状は、我々の社会における富と貧の間の深い格差を反映しています。ごく最近の報告書[10]によれば、今日、この格差は恐れられていたよりもはるかに大きくなっており、8人の男性が、人類の最貧困層の半分を構成する36億人と同じ富を所有している。過去20年間に、統計物理学と確率論の文脈で富の分布を導き出すためにいくつかの理論モデルが開発され、しばしば単純な基礎的ダイナミクスを持つマルチエージェントの視点が採用された [11、12、13、14、15、16、17]。この線に沿って進むと、もし個人の富を成功の代理として考えるなら、人々の間のその深い非対称性と不平等な分布は、才能、スキル、能力、知能、能力における自然の違いの結果であるか、彼らの意志的、勤勉、決意の尺度であると主張できるかもしれません。このような前提は、間接的に、いわゆる能力主義のパラダイムの基礎となっている。この前提は、社会が仕事の機会、名声、名誉を与える方法だけでなく、政府が資源や資金を最もふさわしいと思われる人々に割り当てる際に採用する戦略にも影響を及ぼしているのである。しかし、上記の結論は、上に挙げた人間の特徴や資質が母集団の間で正規分布している、すなわち与えられた平均を中心に対称的なガウス分布に従うという、受け入れられている証拠と厳密に対照的であるように思われる。例えば、IQテストによって測定される知能は、このパターンに従っている。平均IQは100だが、IQが1,000や10,000の人はいないのだ。平均より長い時間働く人と短い時間しか働かない人がいますが、他の人の何億倍も働いている人はいません。
一方、個人生活や職業生活における成功や失敗を決定する上で、偶然性、運、あるいはより一般的なランダム要因が基本的な役割を果たすという証拠が、今日ますます増えてきている。特に、科学者が最大のヒット作を出版する確率はキャリアを通じて同じであること [18]、苗字のイニシャルが早い人は一流大学のテニュアを得る確率が著しく高いこと [19]、学者によって集められた書誌指標の分布は、出版か消滅かのインフレーション機構に関連する乗法的現象に伴う偶然とノイズの結果であるかもしれないこと [20]、 などが示されている。アルファベット順に並べられたリストにおける自分の位置が、過剰に利用されている公共サービスへのアクセスを決定する上で重要かもしれないこと [21]; ミドルネームのイニシャルが知的パフォーマンスの評価を高めること [22]; 発音が簡単な名前の人は発音しにくい名前の人よりも肯定的に判断されること [23]; 高貴な響きの名字を持つ人は従業員よりも管理職として働くことが多いこと[24]、男性的な名字を持つ女性は法曹界でより成功すること[25]、世界中の人の所得のばらつきの約半分は居住国とその国の所得分布によってのみ説明できること [26] など。CEOになる確率は名前や生まれ月に強く影響されること [27, 28, 29]、革新的なアイデアは脳のネットワークにおけるランダムウォークの結果であること [30] 、癌になる確率でさえ、輝かしいキャリアを切るのは主に単純な不運によること [31, 32]などです。最近の生涯生殖成功に関する研究は、形質の変異が集団の運命を左右するとしても、運はしばしば個人の人生を支配することを示し、これらの発言をさらに裏付けている[33, 34]。
近年、統計学者でリスクアナリストのNassim N. Taleb [35, 36]、投資戦略家のMichael Mauboussin [37] 、経済学者のRobert H. Frank [38] など多くの著者が、金融取引、ビジネス、スポーツ、芸術、音楽、文学、科学、その他多くの分野における運と技術の関係についていくつかの成功作で探求している。彼らは、偶然の出来事は、多くの人々がかつて想像していたよりもはるかに大きな役割を果たすという結論に達している。というのも、私たちが現在生活し、働いているような競争の激しい場所や「勝者総取り」の市場では、優れた業績を上げている人はほとんど常に極めて優秀で勤勉な人だからです。つまり、才能と努力だけでは十分ではなく、適切な時に適切な場所にいなければならないという結論になる。つまり、運も重要なのです。たとえ成功者が運の役割を過小評価しているとしても。これは、偶然性が微妙な形で作用することが多いため、成功が必然であったかのような物語を構築することが容易であるためである。タレブはこの傾向を「物語の誤謬」 [36] と呼び、社会学者のポール・ラザースフェルドは「後知恵バイアス」とい う用語を採用している。社会学者でネットワーク科学のパイオニアであるダンカン・J・ワッツは、近著『Everything Is Obvious: Once You Know the Answer』[39]において、人々が異常に成功した結果を観察し、それを努力と才能の必要な産物と考えるときに、物語の誤謬と後知恵バイアスが特に強力に作用すると示唆しているが、それらは主に複雑で織りなす一連のステップから生まれ、それぞれが先例によって依存しており、それらのうちどれか一つが違っていたらキャリア全体や人生の軌道もほぼ間違いなく違っていたと思われるのだ。この議論は、数年前にワッツ自身が他の著者と共同で行った、人工的な音楽市場における未知の曲の成功が曲自体の品質と相関しないことが示された、重要な実験研究の結果にも基づいている[40]。そして、このことは、より最近の別の研究でも示されているように、あらゆる種類の予測を明らかに困難にしている[41]。
本論文では、エージェントベースの統計的アプローチを採用することで、成功するキャリアにおける運と才能の役割を現実的に定量化することを試みる。第2章では、才能のガウス分布[42]と成功と失敗の双方に対する乗法的ダイナミクス[43]という最小限の仮定に基づいて、「才能対運」(TvL)モデルと呼ぶ、あるグループの40年の就業期間におけるキャリアの発展を模倣する単純なモデルを提示する。このモデルは、最も成功した個人を選択する際に、実はランダム性が基本的な役割を果たしていることを示している。確かに、才能のある人は、そうでない人に比べて、生涯を通じて金持ちになったり、有名になったり、重要な人物になったりする可能性が高いことは予想される。しかし、これはあまり直感的な根拠ではないが、平均的なレベルの才能を持つ普通の人々は、生涯を通じて幸運に恵まれる限り、最も才能のある人々よりも統計的にはるかに成功する(すなわち、成功のべき乗則分布の尾部に配置される)運命にあるのである。この事実は、文献[35, 36, 38]で指摘されているように、一般的に経験されていることであるが、我々の知る限り、ここで初めてモデル化され、定量化されたものである。
平均的な才能を持つ人々の成功は、「実力主義」パラダイムや、その分野で最も優れていると考えられる人々により多くの報酬、機会、栄誉、名声、資源を与えるあらゆる戦略やメカニズムに強く挑戦している [44, 45]。重要なのは、大多数の場合、誰かの才能に関するすべての評価は、その人のパフォーマンスや、スポーツ、ビジネス、金融、芸術、科学など、私たちの社会の特定の分野における到達結果だけを見て、事後的に行われるということです。このような誤解を招く評価は、原因と結果をすり替えることになり、単に最も幸運な人たちを最も才能のある人として評価することになる[46, 47]。このような観点から、これまでの研究において、このような「素朴な能力主義」に対する警告がなされ、経営、政治、金融など多くの異なる文脈におけるランダムな選択に基づく代替戦略の有効性が示された[48, 49, 50, 51, 52, 53, 54, 55]。セクション3では、我々のアプローチの応用例として、科学研究の文脈で考えられる公的資金の帰属スキームを比較する。我々は、「素朴な」能力主義的な分配戦略を含むいくつかの分配戦略の効果を研究し、コミュニティにおける最も才能ある人々の成功の最低水準と、結果として生じる公的支出の効率性の両方を高めるための新しい方法を模索することを目的としている。また、一般的には、教育や所得水準といった環境からもたらされる機会(すなわち、個人の出身国や社会的文脈に依存する外部要因)が、成功の確率を高める上でどのように重要であるかを探求している。最後に結論として、本論文は終了する。

図1: シミュレーションの初期設定の一例。本論文で紹介するすべてのシミュレーションは,NetLogoエージェントベースモデル環境 [56]で実現された.N = 1000の個体(エージェント)は,異なる才能(知能,スキルなど)を持ち,周期的な境界条件を持つ201x201パッチの正方形の世界内の定位置にランダムに配置されている.数十年にわたる各シミュレーションの間、彼らは一定数NE個の幸運(緑丸)と不運(赤丸)のイベントにさらされ、それらはランダムな軌道(ランダムウォーク)を辿って世界を移動する。この例では、NE = 500
2 The Model
このモデルは、幸運または不運なランダムイベントの影響を受けた人々のグループのキャリアの進化を記述することを目的として、非常に単純な仮定の小さなセットに基づいて構築されています。才能Ti(知能、技能、能力など)が与えられた平均mTを中心に標準偏差σTで区間[0, 1]に正規分布し、周期的境界条件(すなわち、トロイド型トポロジー)を持つ正方形の世界(図1参照)内の固定位置にランダムに置かれ、ある数の「動く」事象(点で示す)に囲まれたNE人について考える(誰かが幸運、誰かが不運)(中立事象は個人の人生には関係ないのでこのモデルでは考慮していない)。図1では、これらの事象を色付きの点として報告している。幸運なものは緑色で相対的な割合pLで、不運なものは赤色で割合(100-pL)で示している。イベントポイントの総数NEは一様に分布しているが、もちろんこのような分布が完全に一様になるのはNE→∞のときだけである。このシミュレーションでは、通常、NE ∼ N/2とする。したがって、各シミュレーションの始めには、世界のさまざまな地域にラッキーまたはアンラッキーのイベントポイントがよりランダムに集中し、他の地域はより中立的となるであろう。正方格子である世界の中の点がさらにランダムに移動しても、このモデルの基本的な特徴は変わらない。つまり、個人はその才能に関係なく、生涯にわたって異なる量の幸運または不運な出来事に晒される。
一回のシミュレーションでは、労働寿命Pを40年(20歳から60歳まで)とし、時間ステップδtを6ヶ月とする。シミュレーションの始めに、すべてのエージェントは、同じ量の資本Ci = C(0) ∀i = 1, ..., Nを与えられ、これは彼らの成功/富の開始レベルを表している。この選択は、誰にも初期的な利点を与えないという明白な目的を持つ。エージェントの才能は時間に依存しないが、エージェントの資本は時間と共に変化する。このモデルの時間発展、すなわち、エージェントの寿命の間、すべてのイベントポイントは世界中をランダムに移動し、その際、あるエージェントの位置と交差する可能性がある。より詳細には、各イベントポイントは各時刻にランダムな方向へ2パッチの距離を移動する。イベントポイントがエージェントを中心とした半径1パッチの円の中に存在するとき、ある個体に対して交差が発生したと言う(交差後にイベントポイントが消えることはない)。このような事象の発生によって、ある時間ステップt(すなわち、6ヶ月ごと)に、あるエージェントAkには3つの異なる可能な行動が存在することになる。
- エージェントAkの位置を遮るイベントポイントがない:これは、過去6ヶ月間に関連する事実が起こらなかったことを意味し、エージェントAkは何も行動していないことを意味します。
- 幸運な出来事がエージェントAkの位置を横切る:これは、過去6ヶ月間に幸運な出来事が起こったことを意味する(参考文献[30]に従い、ここでは革新的なアイデアの生産もエージェントの脳内で起こる幸運な出来事と考えられることに注意);結果として、エージェントAkは才能Tkに比例して確率的に自分の資本/成功を倍増させる。Ck(t) = 2Ck(t - 1) となるのは、rand[0, 1] < Tk の場合、つまりエージェントが幸運から利益を得るほど賢い場合のみである。
- 不運な出来事がエージェントAkの位置を横取りする:これは、過去6ヶ月間に不運な出来事が起こったことを意味する。その結果、エージェントAkの資本/成功は半分になる、すなわち、Ck(t) = Ck(t - 1)/2.
これまでのエージェントのルール(不運な出来事の場合は初期資金を2倍、幸運な出来事の場合はエージェントの才能に比例して2倍にするという選択を含む)は、意図的にシンプルにしてあり、広く共有できると考えられる。なぜなら、人生における成功は、非常に急速に成長したり減少したりする性質を持っているという常識に基づくものであるためだ。さらに、これらのルールは、高い才能を持つ人ほど、運によってもたらされる機会(頭脳に生まれた良いアイデアを活用する能力を含む)をより良く活用することができるため、大きなアドバンテージとなる。一方、交通事故や突然の病気などは、常に不運な出来事であり、才能は関係ない。この点で、「才能」の定義を「チャンスをつかむ可能性を高めるあらゆる資質」とした方が、より効果的に一般化できる。つまり、「才能」とは、知性、技術、頭の良さ、頑固さ、決断力、努力、リスクテイクなど、広い意味での「才能」である。以下に述べるのは、優れた才能を持つという利点は、非常に高度な成功に到達するための必要条件ではあるが、十分条件ではない、ということである。
2.1 Single run results
このサブセクションでは、典型的なシングルランシミュレーションの結果を示します。実際、このような結果は非常にロバストであり、後で示すように、我々のモデルから得られる一般的なフレームワークをほぼ代表していると考えることができる。N = 1000エージェントで、資本金C(0) = 10(無次元単位)を等しく持ち、平均mT = 0.6 、標準偏差σT = 0.1 の正規分布に従う固定才能Ti ∈ [0, 1] とする(図2を参照のこと)。シミュレーションは、先に書いたように、現実的な期間P = 40年にわたり、6ヶ月ずつの時間ステップで進化し、合計I = 80回の反復が行われます。このシミュレーションでは、NE = 500のイベントポイントを考慮し、幸運なイベントの割合pL = 50%としている。シミュレーションの結果、Figure 3 のパネル (a) に示すように、このモデルの単純な動的ルールでは、大量の貧しい(成功しない)エージェントと少数の非常に豊かな(成功した)エージェントという、資本と成功の不平等な分布を作り出すことができることが分かった。同じ分布を対数スケールでプロットした同図のパネル(b)では、パレート型のべき乗分布が観察され、その尾は関数 y(C) ∼ C -1.27 によってうまくフィットしている。したがって、才能の正規分布にもかかわらず、TvLモデルは、実データとの比較で観察された最初の重要な特徴、すなわち、貧富の差の深さとその規模不変性を捉えることができるようである。特に、我々のシミュレーションでは、500ユニット以上の資本を持つ個人は4人しかおらず、最も成功した20人が資本総額の44%を占めている一方で、人口の約半数は10ユニット以下に留まっている。世界的に見れば、パレートの「80対20」の法則が守られており、80%の人は全体の20%の資本しか持っておらず、残りの20%の人は同じ80%の資本を所有していることになる。この格差は確かに不公平ではあるが、もし、最も成功した人が最も優秀で、他の人よりも多くの資本や成功を蓄積して当然であるならば、ある程度は納得がいくだろう。しかし、本当にそうなのだろうか。図4のパネル(a)と(b)では、それぞれ才能を最終的な資本/成功の関数としてプロットしている(パネル(a)では、資本/成功が不連続な値だけを取っていることに注目しよう:これは、すべてのエージェントに対して等しい整数の初期資本を使用したことによる。) 両パネルとも、最も成功した者が最も優秀な者ではなく、最も優秀な者が最も成功した者でもないことは明らかである。特に、最も成功した個体(Cmax = 2560)の才能 T∗ = 0.61 は平均値 mT = 0.6 よりわずかに大きいだけであり、最も才能のある個体(Tmax = 0.89 )の資本/成功は1単位より小さい(C = 0.625) 。
次の小節で詳しく見るように、このような結果は特殊なケースではなく、むしろこの種のシステムのルールである:最大成功は最大才能と一致することはなく、その逆もまたしかりである。しかも、このような成功と才能の間のずれは不釣り合いで、非常に非線形的である。実際、才能T>T*の人の平均資本はC∼20であり、言い換えれば、中程度の才能を持つ最も成功した人の資本/成功は、彼よりも才能のある人の平均資本/成功の128倍である。もし、ある人たちの大成功の背後に特別な才能がないのであれば、おそらく別の要因が働いているのだろうという結論になる。我々のシミュレーションは、そのような要因が単なる運であることを明確に示している。図5では、すべての人が現役時代に経験した幸運と不運の回数を、最終的な資本と成功の関数として報告している。(a)を見ると、最も成功した人は最も幸運な人であることがわかる(このパネルでは、才能に比例して活用されたものだけでなく、エージェントに起こった幸運な出来事がすべて報告されていることに注意)。逆に、パネル(b)を見ると、あまり成功していない人は、最も不運な人であるという結果になっている。つまり、シミュレーションの結果、成功と才能の間には相関がないものの、成功と運の間には非常に強い相関があることがわかった。また、個人に発生した幸運・不運の数の度数分布の詳細を分析すると、パネル(c)(d)に示すように、指数関数的で、指数は0.64と0.48、平均は1.35と1.66、幸運・不運の発生数の最大値はそれぞれ10と15であることが分かりました。さらに、約16%の人は幸運や不運な出来事を全く経験しない「ニュートラル」な人生であり、約40%の人は幸運や不運な出来事を1種類しか経験しない。
また、最も成功した個人とそうでない個人の成功・資本の時間発展を、彼らの労働人生の40年間(80時間ステップ、6ヶ月ごとに1回)に起こった幸運と不運のシーケンスと比較して見ることも興味深い。これは、Figure 6の左側と右側でそれぞれ観察することができる。図5の(a)とは異なり、この図の下のパネルには、エージェントが才能のおかげで利用することができた幸運なイベントのみが示されている。(a)では、才能はそこそこだが最も成功した人について、人生の前半は幸運な出来事の発生が少なく(下図)、その後、資本水準が低く(上図)、30から40時間ステップの間に(つまり、40歳直前に)突然有利な出来事が集中していることが明確に示されている。 これは、最後の10ステップ(つまり、エージェントのキャリアの最後の5年間)で指数関数的に増加し、C = 320からCmax = 2560になる。一方、(上下の)パネル(b)を見ると、あまり成功していない個人は、特に不運な人生の後半に、不利な出来事が何度もあり、資本/成功が徐々に減少し、最終的にC = 0.00061となることがわかる。しかし、この貧しいエージェントは、才能T = 0.74を持ち、最も成功したエージェントのそれよりも大きいということは興味深いことである。明らかに、運が良かったのである。もし、最も成功したエージェントが、(平均的な才能にもかかわらず)与えられた機会をすべて利用することができたというのなら、もう一人のエージェントのように不運で機会に恵まれない人生では、大きな才能も不幸の猛威には無力であることもまた事実であろう。この小節で示した1回のシミュレーションの結果は,非常に頑健であり,次の小節で見るように,同じ才能分布で個人の位置を変えて何度もシミュレーションを繰り返しても,わずかな差はあるが,その結果は変わらない.

図2:母集団の才能の正規分布(平均mT=0.6、標準偏差σT=0.1、mT±σTは2点鎖線で示す)。この分布は区間[0, 1]で切り捨てられ、シミュレーション中に変化することはない。
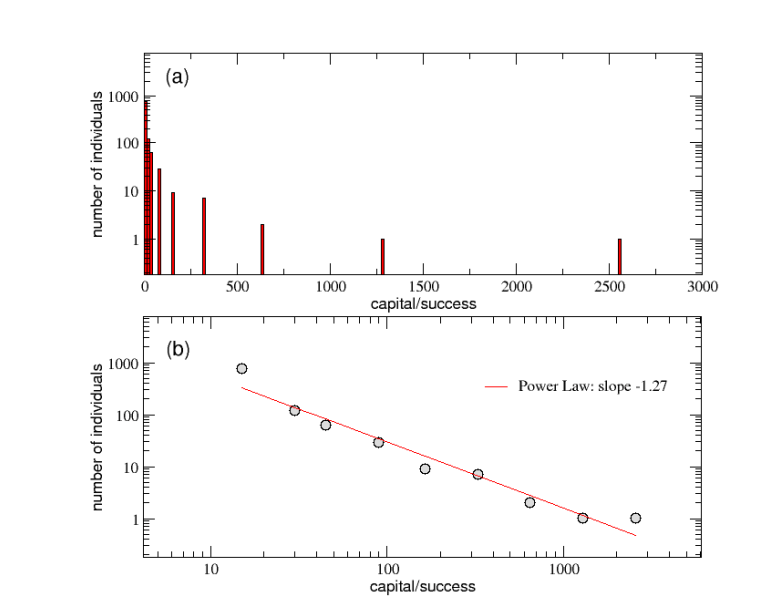
図3: 対数-lin (a) と対数-log (b) スケールの両方で、人口における資本/成功の最終的な分布。才能の分布が正規分布であるにもかかわらず、パネル(b)に見られるように、成功の分布のテールは傾き-1.27のべき乗曲線でうまくフィットさせることが可能である。また、資本と成功の分布はパレートの "80-20 "の法則に従うことが確認された。つまり、人口の20%が全体の80%の資本を所有し、残りの80%は20%の資本を所有しているのである。

図4:パネル(a)では、才能を資本/成功の関数としてプロットしている(より良く可視化するために対数スケールで):最も成功した個人は最も才能のある個人ではないことが明らかである。パネル(b)では、その逆で、資本/成功が才能の関数としてプロットされています。ここでは、Cmax = 2560で最も成功したエージェントは、平均値mT = 0.6よりもわずかに大きい才能を持っているという事実がさらに理解できるでしょう。詳細は本文を参照。
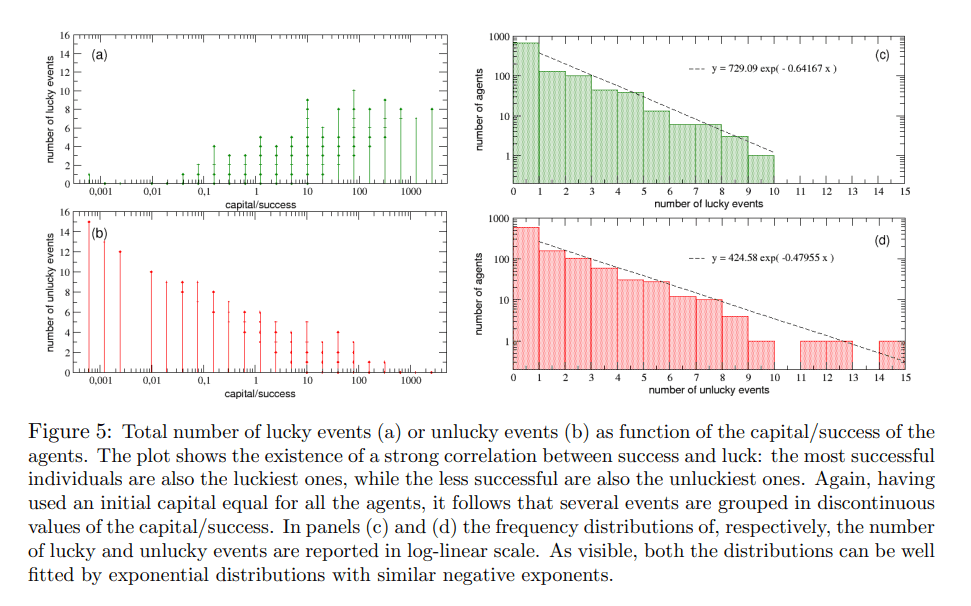
図5: 幸運な出来事の総数 (a) と不運な出来事の総数 (b) を、エージェントの資本/成功の関数として示したもの。このプロットは、成功と運の間に強い相関があることを示している。最も成功した者は最も幸運な者でもあり、そうでない者は最も不運な者でもある。ここでも、すべてのエージェントの初期資本が等しいので、いくつかの事象は、資本/成功の値が不連続になるようにグループ化されていることがわかる。パネル(c)と(d)では、幸運なイベントと不運なイベントの数の頻度分布が、それぞれ対数線形スケールで報告されている。両者の分布は、負の指数が近い指数分布でよくフィットすることがわかる。
2.2 Multiple runs results
このサブセクションでは,それぞれ異なるランダムな初期条件から開始し,100回のシミュレーションを平均化した結果を示す.制御パラメータの値は前のサブセクションで使用したものと同じである。N = 1000 個、mT = 0.6 および σT = 0.1 (正規分布)、I = 80 回 (各回 δt = 6 ヶ月)、C (0) = 10 単位の初期資本、NE = 500 イベントポイント、ラッキーイベントの割合 pL = 50%である。図7のパネル(a)では、100回の実行で収集した全エージェントの最終資本/成功のグローバル分布が対数スケールで示されており、傾き-1.33のべき乗曲線でうまくフィットしている。資本のスケール不変の振る舞いと、その結果生じる個人間の強い不平等は、単一実行のシミュレーションで観察されたパレートの「80対20」ルールとともに、複数実行の場合にも保存されていることがわかる。実際、最も成功した人の資本は40000を超えたので、金持ち(成功者)と貧乏人(失敗者)の間の格差はさらに拡大した。
この結果は、パネル(b)で、最も成功した個人のみ、つまり100回実行した中で最も成績の良かった個人の最終資本Cmaxが、才能の関数として報告されていることから、より理解することができます。最も成績が良かったのは、才能分布の平均値(mT = 0.6)とほぼ一致する才能Tbest = 0.6048のエージェントで、資本Cbest = 40960のピークに到達した。一方、最も成功した人の中で最も才能のある人は、才能Tmax=0.91で、資本Cmax=2560を蓄積し、Cbestの6%にしか達しない。この点をより詳しく説明するために、図8(a)に、100回の実行で計算されたベストパフォーマーの才能分布をプロットしてある。このことは、大きな成功を収めるには中程度の才能が必要であることを確認する一方で、それがほとんど十分でないことも示している。なぜなら、最高の才能を持つエージェント(例えば、T > mT + 2σT 、すなわちT > 0.8 )は、3%のケースでしかベストパフォーマーとならず、その資本/成功はCbestの13%を超えることがないからである。
図 8 (b) では、同じ分布(PDF を得るために単位面積に正規化)を 10000 回にわたって計算し、その真の形状を評価し ている。平均 Tav = 0.667 と標準偏差 0.09 のガウス G(T) でうまくフィットしているように見える(実線)。これは、ベストパフォーマーの才能分布が、本来の才能分布に対して、才能軸の右側にシフトしていることを確実に確認することができる。より正確には、区間[T, T +dT]に才能を持つ個人をベストパフォーマーの中から見つける条件付き確率P(Cmax|T) = G(T)dT は才能Tに応じて増加し、中程度の才能Tav = 0.66 のあたりで最大となり、才能が高くなると急速に減少することを意味している。つまり、成功の頂点にいる中程度の才能の持ち主を見つける確率は、そこに非常に優れた才能の持ち主を見つける確率よりも高いのである。したがって、P(Cmax|T)のガウス型は、非常に高いレベルの成功に到達するためには、才能よりも運が重要であることの証明であると結論づけることができる。また、最も才能のある人の 100 回の平均成功資本 Cmt ∼ 63 と、平均 mT に非常に近い才能を持つ人の平均成功資本 Cat ∼ 33 を比較することも興味深い。いずれの場合も非常に小さな値(初期資本C(0)=10よりは大きい)であるが、Cmt > Catであることは、たとえ成功の頂点に中程度の才能の人がいる確率が、そこに非常に優れた人がいる確率よりも高いとしても、各ランの最も優れた人は平均的に中程度の才能の人よりも成功が多いことを示す。一方、才能T > 0.7(すなわち、平均から1標準偏差より大きい)かつ最終的な成功/資本Cend > 10の個人の100ランの平均割合を見ると、才能T > 0.7のすべてのエージェントに関して計算されます。 このことは、才能あるエージェントの3分の1しか最終的な資本が初期資本を上回らないため、集団の中で最も才能ある人々の総パフォーマンスは、平均して比較的小さいままであることを示している。
いずれにせよ,100回のシミュレーションで絶対的なベストパフォーマーは,才能Tbest = 0.6で,平均と完全に一致しているが,最終的な成功Cbest = 40960はCmtの650倍であり,最も才能ある2/3の成功Cend < 10の4000倍以上であるということは事実である.これは、物語の最後に、彼女が他の人たちよりも運がよかったというだけのことである。図9には、現役時代における彼女の資本と成功の増大が、特別な才能がないにもかかわらず、彼女がそのキャリアにおいて活用することができた幸運な(そして幸運でしかない)出来事の印象的なシーケンスとともに示されている。要約すると、TvLモデルは、その単純さにもかかわらず、冒頭で述べたように、我々の社会における富と成功の大きな不平等分布を特徴づける特徴の多くを説明することができるようである(人間の才能のガウス分布とは明らかに対照的である)。同時に、このモデルは、優れた才能は成功するキャリアを保証するのに十分ではなく、その代わりに、才能のない人が成功の頂点に立つことが非常に多いことを定量的に示しており、これも実生活で頻繁に見られる「様式化された事実」である[35, 36, 38]。中程度の才能の人が、はるかに才能のある人よりもはるかに大きな栄誉と成功を収めることが(しばしば)あり得ることを直感的に説明する重要なポイントは、我々のシミュレーションから得られた、隠れた、しばしば過小評価される運の役割である。しかし、我々の発見の本当の意味を理解するためには、マクロな視点とミクロな視点を区別することが重要である。
実際、ミクロな視点から見ると、TvLモデルの力学的ルールに従って、才能のある人は、中程度の才能の人よりも、先験的に高いレベルの成功に達する確率が高く、どんな機会が来てもそれを把握する能力が高いからである。もちろん、そのような機会を得るためには、運の助けも必要である。したがって、一個人の観点からは、幸運な出来事の発生をコントロールすることは(定義上)不可能であるため、成功の確率を高めるための最善の戦略は、(どのような才能レベルであっても)個人の活動、アイデアの生産、他者とのコミュニケーションを広げ、多様性と相互理解を求めることであると結論づけることができるだろう。つまり、オープンマインドな人間であること、他者と接する準備ができていることが、幸運な出来事(個人の才能を生かすこと)に遭遇する確率を最も高くするのである。一方、社会全体のマクロな視点から見ると、中程度の才能を持つ人がトップレベルの成功を収める確率は、非常に優秀な人が成功する確率よりも高い。なぜなら、中程度の才能を持つ人は、個人のアプリオリ確率が低いにもかかわらず、数がはるかに多く、運も手伝って、大きな成功に到達する統計的優位性を世界的に持っているからである。次のセクションでは、このようなマクロ的な視点から、母集団の中で最も才能のある人々の平均的なパフォーマンスを向上させ、賞や資源をより効率的に配分するための新しい、より効率的な戦略や政策を詳細に検討するために、我々のモデルが提供する可能性を探ります。実際、最も優秀な人々は社会の進歩と革新の原動力であり、彼らの成功のレベルを向上させることができる政策は、集団に有益な効果をもたらすと期待される。
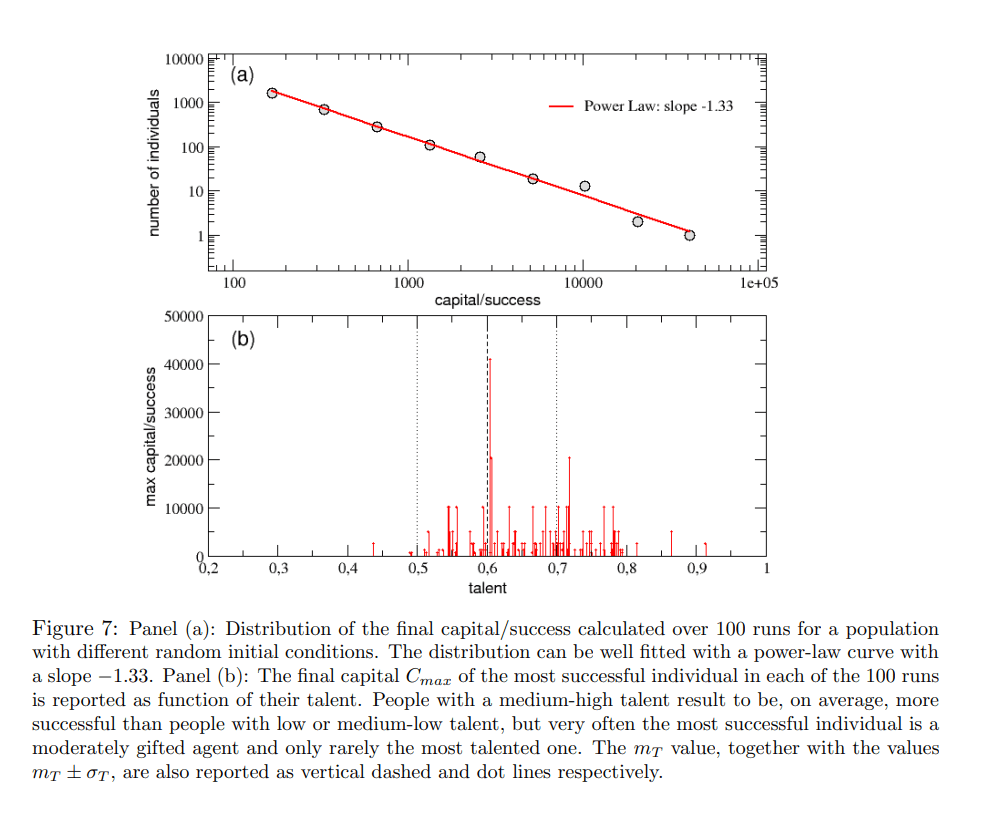
図 7:パネル(a)。異なるランダムな初期条件を持つ母集団に対して、100回の実行で計算された最終的な資本/成功の分布。この分布は、傾き-1.33のべき乗則曲線でうまくフィットすることがわかる。パネル(b): 100回の実行で最も成功した個体の最終資本Cmaxを、その才能の関数として報告する。中程度の才能の持ち主は、平均して低・中程度の才能の持ち主よりも成功するが、最も成功した人物は中程度の才能の持ち主であることが非常に多く、最も才能のある人物であることは稀であることが分かる。mT値は、mT±σT値とともに、それぞれ縦の破線と点線で報告されている。

図 8: (a) 100 回の各ランで最も成功した個体(ベストパフォーマー)の才能の分布。(b) 10000回の実行で計算された最も成功した個体の才能の確率分布関数:平均0.667、標準偏差0.09の正規分布でうまく適合している(実線)。母集団における才能の正規分布の平均値mT=0.6は、両パネルにおいて縦の破線で示されており、比較のために報告されている。
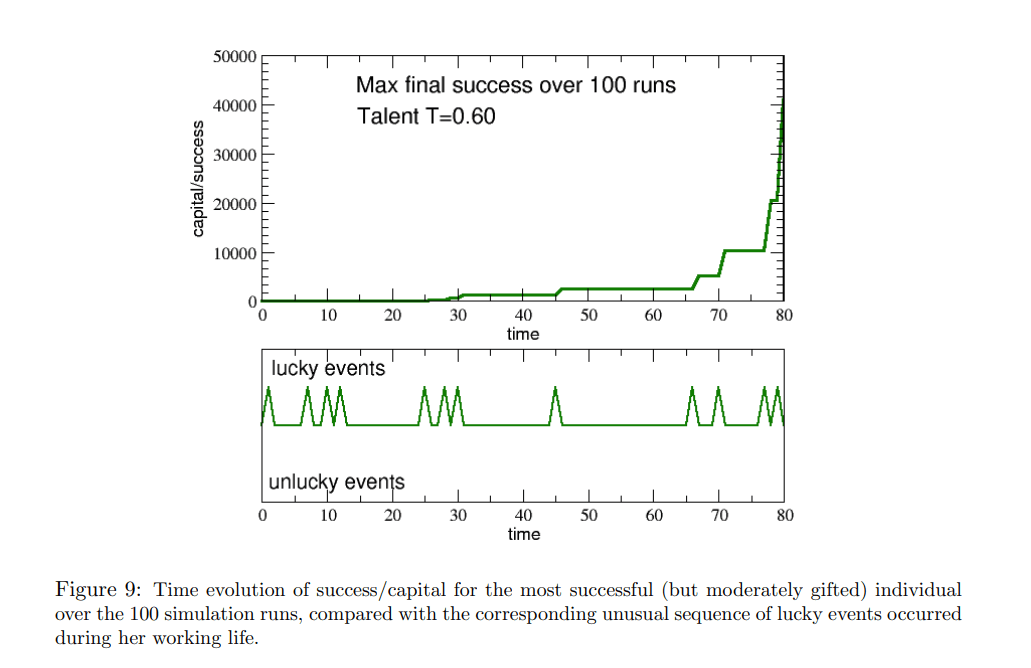
図9:100回のシミュレーションを行った最も成功した人(ただし、才能は中程度)の成功と資本の時間変化と、それに対応する現役時代に起きた幸運な出来事の異常な連続との比較。
3 Effective strategies to counterbalance luck (運を逆手に取った効果的な戦略)
前節で示した結果は、冒頭で述べた実証的な証拠と強く一致している。この証拠によると、才能、技能、能力、知能、努力、決意の自然な差が唯一の成功の原因であるという素朴な能力主義の仮定に確固たる疑問を呈している。これまで述べてきたように、運もまた重要であり、非常に重要な役割を果たすことがある。解釈のポイントは、個人の資質は測定が困難であるため(多くの場合、厳密な用語でほとんど定義されていない)、栄誉、資金、報酬を与えるために用いられる能力主義の戦略は、しばしば個人の富や成功の観点から評価される個人のパフォーマンスに基づいていることである。結局、こうした戦略はさらなる強化作用を発揮し、最も幸運 な個人の富や成功を正のフィードバック・メカニズムによって 増進させるが、これは有名な「金持ちはより金持ちになる」プロセ ス(「マシュー効果」[57、58、59]としても知られる)に似ており、最終 的に不公平な結果をもたらす。例えば、一定額の資金を自由に使える公的資金による研究助成団体を考えてみよう。研究の平均的なインパクトを高めるには、少数の明らかに優秀な研究者に大規 模な助成金を与えるのと、多数の一見普通の研究者に小規模な助成金を与えるのと、 どちらが効果的でしょうか。最近の研究 [44] では、出版物を含む科学的インパクトの4つの指標の分析に基づき、 インパクトは資金と正の相関があるが、弱い相関に過ぎないことが判明しました。特に、1ドルあたりのインパクトは、大規模な助成金を獲得している研究者ほど低く、助成金の増額を受けた研究者のインパクトは有意に増加しませんでした。この研究の著者らは、科学的インパクト(論文発表によって反映される)は資金によって弱く制限されるだけであると結論付け、「優秀さ」よりもアイデアの多様性をターゲットとした資金戦略がより生産的である可能性を示唆しています。さらに最近の論文[60]では、生産された論文の量とその科学的影響の両方において、 研究費の集中は一般的に限界収益の逓減をもたらすこと、また、最も多くの研究費を得て いる研究者が、生産高と科学的影響の点で際立っていないことを示しました。実際、影響力のある論文で測定されるインパクトは、科学者の一連の論文の中でランダムに分布しているという最近の発見 [18] を考慮すると、このような結論は驚くべきことではありません。つまり、もし運が重要なら、そして運が私たちが認める以上に重要なら、特に事後的に実力を評価しようとした場合、実力主義的戦略が期待よりも効果がないことが明らかになるのは不思議なことではありません。先行研究[48, 49, 50, 51, 52, 53, 54, 55]では、すでにこの種の「素朴な実力主義」に対する警告があり、経営、政治、金融においてランダムな選択に基づく代替戦略の有効性を示していた。TvLモデルは、このような観点と一致して、運が重要であり、セレンディピティが重要な発見の原因となることが多い世界において、最も優秀な人々の成功の最低レベルをいかに高めることができるかを示すものである。
3.1 Serendipity, innovation and efficient funding strategies (セレンディピティ、イノベーション、効率的な資金調達戦略)
「セレンディピティ」という言葉は、研究者が何かを探しているときに、偶然に予想外の有益な発見をすることが非常に多いという歴史的な証拠を指すものとして、文献上よく使われている[61, 62]。Alexander Fleming のペニシリンから Marie Curie の放射能まで、電波天文学者 Arno Penzias と Robert Woodrow Wilson の宇宙マイクロ波背景放射から Andre Geim と Kostya Novoselov のグラフェンまで、幸運な機会によってなされた発見の逸話は枚挙に暇がないほどである。ごく最近の例を挙げると、人体内の液体で満たされたチャネルのネットワークは、これまで知られていなかった器官である可能性があり、体内のがん細胞の輸送を助けるようですが、日常的な内視鏡検査から偶然発見されました[63]。したがって多くの人々は、好奇心主導の研究は常に資金提供されるべきだと思っており、誰もそれがどこにつながるかを本当に知ることや予測できないのです [64].
セレンディピティの役割を定量化することは可能か?セレンディピティを刺激する最も効率的な方法はどれでしょうか?セレンディピティには様々な形があり、それを制約したり定量化したりすることは困難です。そのため、これまで学術的な研究では、科学におけるセレンディピティは主に哲学的な考えとして注目されてきました。しかし、状況は変わりつつある。欧州研究評議会は最近、生化学者のOhid Yaqubに170万USドルの助成金を与え、科学におけるセレンディピティの役割を定量化させた[65]。Yaqubはセレンディピティを4つの基本的なタイプに分類することが可能であり[66]、その発生に影響を与える重要な要因があるかもしれないことを見いだした。彼の結論は、卓越性を追求し多様性を排除する、一般的に採用されている一見実力主義的な戦略は、失われ非効率になる運命にあるようだと主張する以前の著作 [67, 68, 69, 70, 71, 72] で展開された考えと一致するようである。その理由は、当初はあまり期待できないように見えても、セレンディピティのおかげで事後的には極めて革新的となりうる研究を、先験的に切り捨ててしまうからである。この観点から、この小節では、さまざまな資金調達シナリオの有効性を探るために、運(したがってセレンディピティも)を自然に組み込んだTvLモデルを、政策のための定量的ツールとして使用したいと思う。特に、上述のように、平均的な才能を持ちながら運の悪い人が、才能を持ちながら運の悪い人よりも成功することが多い状況においては、最も進歩的で革新的なアイデアを生み出すと期待される最も才能ある人々にも最低限の成功を維持するための資金戦略の効率性を評価することが重要である。
2.2 節で用いたのと同じパラメータ設定、すなわち N = 1000、mT = 0.6、I = 80、δt = 6、C(0)を用いて、最も進歩的で革新的なアイデアを生み出す。N = 1000, mT = 0.6, σT = 0.1, I = 80, δt = 6, C(0) = 10, NE = 500, pL = 50, 100 回のシミュレーションを行った後,与えられた総資金 FT を異なる基準で個人別に定期的に配分する場合を考えてみよう.例えば、資金は以下のように割り振られる。
- 研究の多様性を促進するために、全員に均等に配分する(平等主義的基準)。
- 最も成功した(「ベスト」)個人の一定割合にのみ配分する(エリタリアン基準)。これは、過去の業績に応じて人々に資金を配分するため、以前は「素朴な」能力主義と呼ばれていた。
- ある一定の割合の最も成功した個人に「プレミアム」を配分し、残りの金額を他のすべての人に均等に配分する方法(混合基準)。
- 無作為に選ばれた一定割合の個人のみに分配する(選択的無作為基準)。
現実的には、各シミュレーションの実行期間である40年の間に、5年ごとに資本金FTが分配され、FT /8単位の資本金が随時割り当てられると想定している。このように定期的に資金を投入することで、最も優秀なエージェントに最低限のリソースを提供することを意図している。したがって,採用した資金戦略の有効性を示す良い指標は,才能T > mT + σTを持つ個人のうち,最終的な成功/資本が初期値より大きい,すなわちCend > C(0)となる割合PT(100回のシミュレーションの平均)であろう.この割合は、2.2節で紹介した複数回実行シミュレーションで既に計算されている。そこでは,資金がない場合,最高のパフォーマンスは平均に近い才能を持つ非常に幸運なエージェントによって獲得され,最も才能のある人々の資本/成功は常に非常に低いままであることを示した.特に,T > 0.7のエージェント総数のうち,PT0 ∼ 32%のエージェントだけが,シミュレーションの終了時に,初期値よりも大きな資本/成功に到達している.したがって,異なる資金調達戦略の効率を比較するために,有能な人材の平均的な割合PTが,そのキャリアにおいて,初期の資本/成功を増加させる割合を,PT0に対して計算する必要がある.この増分は、P*T=PT-PT0と定義しよう。後者は非常に頑健な指標であり、100回のシミュレーションを繰り返しても、P∗Tの値の変動は2%以下であることが確認されている。最後に、P∗Tと40年間に全エージェントに分配された総資本FTの比率を考えると、投下資本1単位あたりの十分に成功した人材の増加量を定量化する効率指標Eを得ることができ、E = P∗T /FT で定義される。
図10に示した表では,それぞれ異なる資金配分戦略で得られた効率指数(2列目)と,それに対応するPT(3列目)およびP∗T(4列目)を報告している.各ランに投下された総資本FTも最後のコラムで報告されている。効率指数Eは最大値Emaxで正規化し、Enorm=E/Emaxの値が小さい順に並べてある。図11では,Enormの同じスコアが,採用した資金調達戦略の関数として,ヒストグラムの形で報告されている.2%未満の変動しか示さないPTの統計的な頑健性のおかげで,効率性指標Enormの結果は特に安定したものとなっている.表と図11の相対ヒストグラムを見ると、最も優秀な人材に報いる(したがって最終的な成功のレベルを上げる)ことが目的であれば、分配の時点ですでに到達した成功のレベルによって選ばれた一部の人材にのみ大きな資本を与えるよりも、すべての人材に定期的に(たとえ少額でも)同額の資本を分配する方がずっと便利であることが分かる。一方、ヒストグラムは、5年ごとに1単位の資本をすべての個人に割り当てる「平等主義」基準が、Enorm = 1(すなわちE = Emax)であり、資金分配の最も効率的な方法であることを示している。8000単位という比較的小さな投資FTで、「資金なし」の場合と比較して、成功した才能ある人々の割合を2倍にすることができ、その割合はPT0 = 32.05% から PT = 69.48% となりP * T = 37.43% の純増となる。また,総投入資本の増加(例えば,平等枠を2個または5個に設定)を考慮すると,正規化効率がEnorm = 1からEnorm = 0.74,Enorm = 0.37へと徐々に低下しても,この戦略によって最終的に成功する有能な人材の割合PTがさらに増加する(69.48%から84.02%,94.40%)ことが確実である.一方、5年ごとに成功者のうち優秀な50%、25%、あるいは10%にのみ資金(5、10、15、20ユニット)を割り当てる「エリタリアン」戦略は、いずれもEnorm < 0.25でランキングの最下位にある。これらのケースでは、「資金なし」に対する成功者の純増P * Tは非常に小さく(ほとんどすべてのケースで20%未満)、平等主義戦略のそれと比較すればはるかに大きな投資資金に対してしばしば過小である。これらの結果は、この種のアプローチは見かけ上、すなわち素朴に実力主義であるというテーゼを補強するものである。
注目すべきは、「混合」基準を採用した場合、つまり、「実力主義的」な資金分配を一定の割合、たとえば25%に割り当て、残りの資金を残りの人々に平等に分配した場合、「単純な実力主義」アプローチと比較して効率指標値で良いスコアを取り戻すことができる点である。しかし、この戦略のパフォーマンスは、「平等主義」基準を追い越すことはできない。例えば、資金表の6行目と4行目の比較で明らかなように、同じ16000ユニットの全体投資にもかかわらず、混合基準で得られたPTの値は平等主義アプローチで得られた値(84.02%に対して70.83%)を大きく下回り、対応する効率指数Enormの値(0.74%に対して0.55)でも確認されるように、混合基準で得られた値は平等主義アプローチで得られた値を大きく下回るままである。心理的要因(本研究ではモデル化していない)を考慮すると、混合戦略は平等主義的な戦略に対して再評価される可能性がある。実際、より成功した個人に割り当てるプレミアム報酬は、すべてのエージェントをより大きなコミットメントへと誘導し、一方、均等配分された部分は、個人レベルでは、多様性を育み、不運な才能ある人々に自分の可能性を表現する新しい機会を提供し、総体レベルではセレンディピティを養い、研究および社会全体の進歩に貢献する、という2つの役割を果たすであろう。資金調達戦略の表を改めて見ると、総合ランキングのベスト 3 のうち 2 つを占めるランダム戦略が驚くほど効率的であることも強調すべき点である。例えば、無作為に選ばれた10%の個人のみに5単位の定期的な報酬を与え、総投資額を4000単位とした場合、純増P*T=17、78%となり、エリタリアン戦略で得られたほぼ全ての報酬を上回る結果となった。さらに、無作為に選ばれた人々の割合を25%に増やし、全体の投資額を2倍(10000ユニット)にすると、純増加P*T=35.95%は、効率ランキングで1位となった最高の平等主義戦略で得られたものと同程度になる。この後者のP*Tのスコアは、全く同じ資本(10000ユニット)を全く同じ人数(全体の25%)の個人に分配するエリタリアン的アプローチ(表の12行目参照)で得られた値(P*T=9.03%)の約4倍も大きいことに気づくのは、驚くべきことである。後者は、偶然性が重要な役割を果たす複雑な社会的・経済的状況では、ランダムな選択に基づく代替戦略の効率は、「素朴な能力主義」アプローチに基づく標準戦略の効率を容易に追い越すことができることをさらに確認するものである。このような直感に反する現象は、経営、政治、金融ですでに観察されているが([48, 49, 50, 51, 52, 53, 54, 55])、したがって研究費の状況でも新しい証拠が見つかる。
これらの結果をさらに裏付けるために、Figure 12 では、別のシミュレーションの結果を示している。前回のシミュレーションと異なり、100のランのそれぞれに投資された総資本はFT = 80000に固定され、FT /8 = 10000ユニットが5年ごとに、すでに検討した主な資金戦略に従ってエージェントに分配される。表から,平等主義戦略は,最も才能のある人に報酬を与えるのに最も効率的で,その割合PTは100%に近く,すぐにランダム戦略(ランダムに資金を提供する人が50%)と混合戦略(最も成功した25%の人に資本の半分を,残りの半分を残りの人に均等に配分)がそれに続く.逆に、すべてのエリタリアン戦略は再びランキングの最下位となり、真の才能に報いるためには「素朴な実力主義」的アプローチが非効率であることがさらに確認されることになった。この小節で紹介したTvLモデルのシミュレーションの結果は,不運な出来事によってしばしばペナルティを受ける最も才能のある個人の成功の機会を増大させる外部要因(実際,効率的な資金調達政策)の重要性に焦点を当てたものであった.次のサブセクションでは,例えば,教育レベルや,人々が住んでいるあるいは出身する社会的文脈から受けるその他の刺激など,環境の変化によってどの程度新しい機会がもたらされうるかを調査している.

図 10:資金調達戦略 表.異なる目標値を持ついくつかの資金配分戦略(1列目)に対して,正規化効率指数Enormの結果を上から下へ順に報告する(2列目).また,100 回のシミュレーションの平均値として,成功した有能な人材の割合 PT と,「資金なし」の場合に対する純増 P∗ T を,それぞれ 3 列目と 4 列目に報告する.最後に、各実行における総投資額FTが最後の列に示されている。
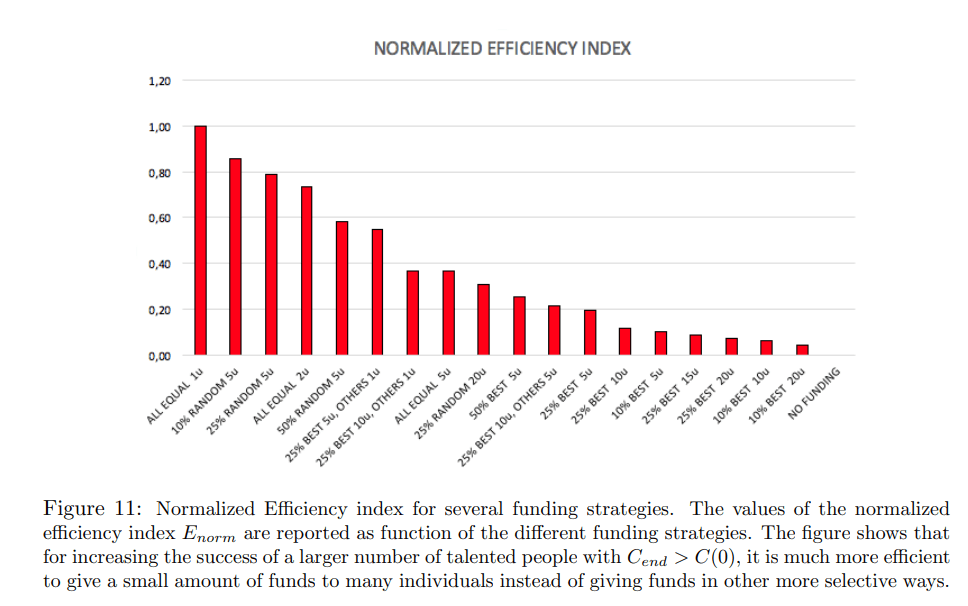
図 11:いくつかの資金調達戦略に対する正規化効率指数。正規化効率指数Enormの値が,異なる資金調達戦略の関数として報告されている.この図から,Cend > C(0)でより多くの有能な人々の成功を高めるためには,他のより選択的な方法で資金を与えるよりも,多くの個人に少量の資金を与える方がはるかに効率的であることがわかる.
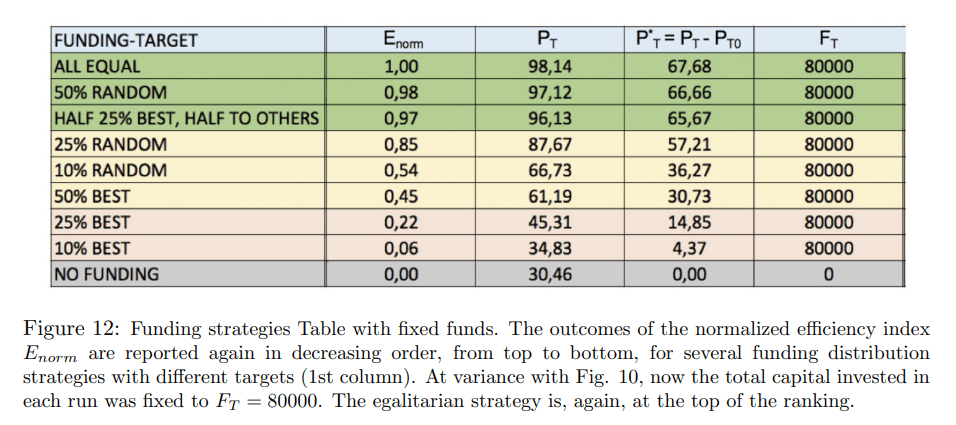
図 12:固定資金による資金戦略表.正規化効率指数Enormの結果は,異なる目標を持ついくつかの資金分配戦略について,再び上から下へ順に報告されている(1列目).Fig.10と異なり,今度は各ランに投下される総資金をFT = 80000に固定した.平等主義的戦略は、再び、ランキングの上位に位置している。
3.2 The importance of the environment (環境の大切さ)
まず、母集団の平均的な教育水準が果たす役割を推定してみよう。TvL モデルでは、才能の正規分布のパラメータを変更することで、後者を得ることができる。実際、個人の才能やスキルが刺激されれば、新しい機会をより効果的に利用できるようになると仮定すれば、才能分布の平均mTや標準偏差σTの増加は、それぞれ平均教育水準の引き上げや最も優秀な人材の育成を目標とする政策の効果として解釈することができるだろう。図13の2つのパネルでは、100回の実験のそれぞれで最も優秀な人が蓄積した最終的な資本/成功を、その才能の関数として報告している。パラメータの設定は 2.2 節と同じであるが(N = 1000, I = 80, δt = 6, C(0) = 10, NE = 500, pL = 50%)才能分布のモーメントが異なっている。特に、パネル(a)ではmT=0.6を変えずにσT=0.2を大きくし、パネル(b)では逆にσT=0.1を残してmT=0.7を大きくしています。どちらの場合も、最大成功率のピークが右にシフトしていることが分かりますが、その内容は異なっています。実際、パネル(a)のようにmTを変えずにσTを大きくすると、より優秀な人が非常に高い成功率を得る可能性が高くなることがわかります。これはポジティブなことであるが、一方で、これは孤立したケースであり、成功者と失敗者の間の格差が拡大することを意味している。次にパネル(b)を見ると、σTを変えずにmTを増やすと、Cbest=327680、才能T=0.8のベストパフォーマーが生まれ、C=163840、T=0.85、T=0.92の他の2人がそれに続くという結果が出ています。これは、この場合にも、より才能のある人が非常に高い成功を収める可能性が高まる一方で、失敗者と成功者の間の格差は以前より小さくなることを意味している。
最後に、両者とも、100 回の実行における最も優秀な人の資本/成功の平均値は、2.2 節で求めた Cmt ∼ 63 と比較して増加していることがわかる。特に、パネル(a)ではCmt ∼ 319、パネル(b)ではCmt ∼ 122となったが、これらの値は特定のシミュレーション実行のセットにかなり敏感である。つまり、才能T > mT + σTを持つ個人の総数に対する、才能T > mT + σTを持ち、最終的な成功・資本Cend > 10を持つ個人の平均割合である(ここで、両ケースにおいて、mT + σT = 0.8であることに注意されたい)。特に、パネル(a)ではPT=38%、パネル(b)ではPT=37.5%であり、基準値PT0=32%(mT=0.6、σT=0.1の才能分布)に対して、わずかに増加することが分かった。まとめると、才能のある人の育成を強化したり、平均的な教育水準を高めたりすることは、予想通り、社会システムに対して何らかの有益な効果をもたらすことが示された。しかし、その一方で、高い才能を持ちながらそれなりの成功を収める人々の平均的な割合の増加は、分析したいずれのケースでも特に顕著ではないようで、したがって、対応する教育政策の結果は、主に孤立した極端な成功例の出現に限定されているようである。
もちろん,教育水準が決まれば,社会環境,つまり,生まれた国や住んだ国が提供する機会の豊富さが,システムのグローバルなパフォーマンスに影響を与えるもう一つの重要な要素であることは明らかである.図14は、前の図と同様の結果であるが、2.2節と同じパラメータ(N = 1000, mT = 0.6, σT = 0.1, I = 80, C(0) = 10, NE = 500)で、ラッキーイベントの割合pLを変えて、それぞれ100回ずつシミュレーションしたものである(なお、この割合pL = 50%と2.2節で設定したことを忘れないように)。パネル (a) では,pL = 80% とした.これは,アメリカのような豊かな先進国のような,刺激的で機会に富む環境をシミュレートするためである [26].一方、パネル(b)では、pL = 20%は、例えば第三世界諸国のように、機会が非常に少なく、刺激の少ない環境の場合を再現している。両図に見られるように、最も成功した人たちの最終的な成功と資本は、その才能の関数として、pLに強く依存する。pL = 80% の場合、(a) のように、才能が中程度のエージェントが、pL = 50%の場合よりも高い成功レベルに達し、Cbest = 163840のピークを記録することができる。一方、最も才能のある人の資本/成功の平均値Cmt ∼ 149は非常に高く、さらに重要なことは、同じことが指標PT = 62.18%(基準値PT0 = 32%に対して約倍)にも当てはまるということで、予想通り、才能ある人は高い割合で幸運なイベントの恩恵を受けているということです。pL = 20%では、まったく異なる結果が得られる。実際、パネル(b)に見られるように、全体の成功のレベルは、2.2節のシミュレーションと比較して非常に低くなり、ピーク値Cbestはわずか5120ユニットとなりました:これは、社会的不平等が減少したことの足跡であり、成功機会の平坦化がもたらす期待どおりの結果です。この結果から、PT指標も最小値に達し、初期の成功レベルを向上させることができた才能ある個人の割合は、平均でわずか8.75%であることがわかる。結論として、本節では、刺激的な環境、豊富な機会、資金や資源の適切な配分戦略が、最も優秀な人材の潜在能力を引き出し、中程度の才能を持つが運の良い人材に対して、より多くの成功の機会を与える重要な要因であることを示してきた。マクロレベルでは、これらの要因に影響を与え、才能ある個人を維持することができる政策は、集団的な進歩と革新を保証するという結果をもたらすだろう。

図13:才能分布のパラメータが異なる集団について、100回の実行で最も成功した個体の最終資本を才能の関数として報告:(a) mT = 0.6, σT = 0.2 (最も才能のある人に対する訓練強化を表す); (b) mT = 0.7, σT = 0.1 (平均教育レベルの上昇を表す).また、対応するmTとmT±σTの値を、それぞれ縦の破線と点線で示した。

図14:ラッキーイベントの割合pLが異なる環境に住む集団について、各100回の実行で最も成功した個体の最終資本を、その才能の関数として報告する。(a) pL = 80%; (b) pL = 20%。mT = 0.6 と mT ± σT 、σT = 0.1 の値もそれぞれ縦の破線と点線で示されている。