import numpy as np
from scipy.special import factorial
import matplotlib.pyplot as plt

def fourier_square(n):
  t = np.arange(-3, 3, 0.01)

  a = np.zeros(n+1)
  b = np.zeros(n+1)

  square_wave = np.ones_like(t)
  for ii in range(0, t.shape[0]):
    if ((t[ii] > 0) * (int(t[ii])%2 == 1) + (t[ii] < 0)*(int(t[ii])%2 == 0)):
      square_wave[ii] = -1
  

  for ii in range(1, n+1):
    cosine = np.cos(np.real(ii) * np.pi * t)
    sine   = np.sin(np.real(ii) * np.pi * t)

    a[ii] = np.polyfit(cosine, square_wave, 1)[0]
    b[ii] = np.polyfit(sine,   square_wave, 1)[0]
  
  square_approx = np.zeros_like(t)
  for ii in range(0, n+1):
    square_approx += a[ii] * np.cos(np.pi * np.real(ii) * t) \
                + b[ii] * np.sin(np.pi * np.real(ii) * t)
    
  plt.plot(t, square_wave, 'k--')
  plt.plot(t, square_approx, 'b')
  plt.show()

  return a, b

if __name__ == '__main__':
  t = np.arange(-3, 3, 0.01)
  
  exp_analytical = np.exp(t)
  
  exp_approx = np.zeros_like(t)
  for ii in range(0, 5):
    exp_approx += (1/factorial(ii))*t**(np.real(ii))
  
  plt.plot(t, exp_analytical, 'k--')
  plt.plot(t, exp_approx, 'b')
  plt.show()
  
  n = np.arange(0, 6)
  plt.plot(n, 1/factorial(n), 'r')
  plt.scatter(n, 1/factorial(n))
  plt.show()
  
  square_wave = np.ones_like(t)
  for ii in range(0, t.shape[0]):
    if ((t[ii] > 0) * (int(t[ii])%2 == 1) + (t[ii] < 0)*(int(t[ii])%2 == 0)):
      square_wave[ii] = -1
  
  plt.plot(t, square_wave, 'k--')
  plt.show()
  
  [a, b] = fourier_square(10)
  [a, b] = fourier_square(100)

import numpy as np
from scipy.special import factorial
import matplotlib.pyplot as plt

import ft

[a, b] = ft.fourier_square(100)

n = np.arange(0, 15)
plt.plot(n, b[n], 'r')
plt.scatter(n, b[n])
plt.show()

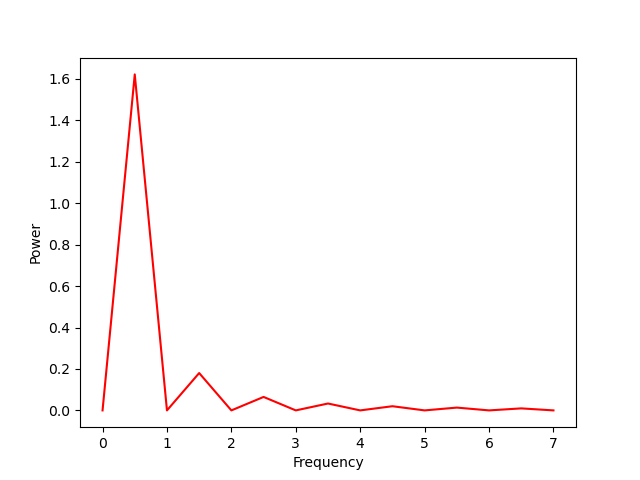
plt.plot(n/2, a[n]**2 + b[n]**2, 'r')
plt.xlabel("Frequency")
plt.ylabel("Power")
plt.show()

import numpy as np
import matplotlib.pyplot as plt
from scipy.special import factorial
import math
from scipy import signal
 
def aave(west, east, south, north, \
    var, lon2, lat2):
  avar = var[(west<=lon2[:, 1]) * (lon2[:, 1]<=east), :, :]
  avar = avar[:, (south<=lat2[1, :]) * (lat2[1, :]<=north), :]
  alat2 = lat2[(west <= lon2[:, 1]) * (lon2[:, 1] <= east), :]
  alat2 = alat2[:, (south <= lat2[1, :]) * (lat2[1, :] <= north)]

  [imt, jmt, tmt] = avar.shape
  numer = np.zeros((imt, jmt, tmt))
  denom = np.zeros((imt, jmt, tmt))
  for k in range(tmt):
    for i in range(imt):
      for j in range(jmt):
        numer[i, j, k] = avar[i, j, k] * math.cos(math.radians(alat2[i, j]))
        denom[i, j, k] = math.cos(math.radians(alat2[i, j]))

  aave_var = np.nansum(np.nansum(numer, 0), 0) / \
             np.nansum(np.nansum(denom, 0), 0)

  return aave_var

def plot_mon_time(time_series, lower = -3, upper = 3, init_year = 1982, fin_year = 2019):
  mon = np.arange(init_year, fin_year+1, 1/12)
  plt.figure
  plt.plot(mon, time_series)
  plt.plot(mon, 0 * time_series, 'k')
  plt.xlim(init_year, fin_year)
  plt.ylim(lower, upper)
  plt.show()

if __name__ == '__main__':
 
  loadfile = 'detrended_ssta_OISST.npz'
  ssta_dataset = np.load(loadfile)
  ssta = ssta_dataset['ssta']
  lon2 = ssta_dataset['lon2']
  lat2 = ssta_dataset['lat2']

  y = ssta_dataset['y']
  m = ssta_dataset['m']

  ssta = ssta[:, :, (1982 <= y) * (y <= 2019)]
  m = m[(1982 <= y) * (y <= 2019)]
  y = y[(1982 <= y) * (y <= 2019)]

  nino34 = aave(190, 240, -5, 5, ssta, lon2, lat2)
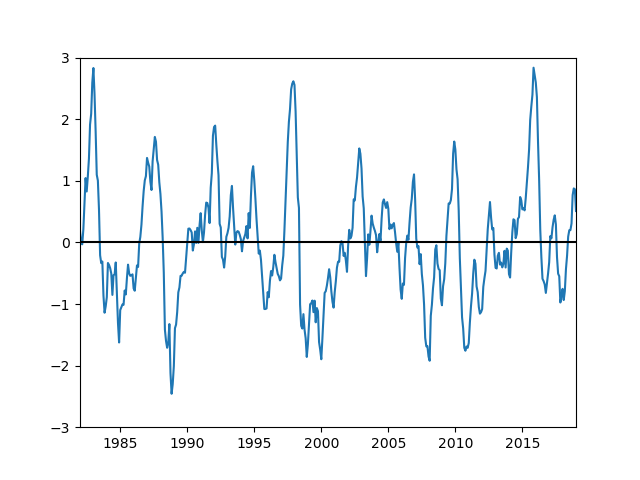
  plot_mon_time(nino34)

  N = nino34.shape[0]
  delta_t = 1

  nino34_k = np.fft.fft(nino34)[1:math.floor(N/2)]

  power = 2 * np.abs(nino34_k)**2 * delta_t / N

  frequency = np.fft.fftfreq(N, delta_t)[1:math.floor(N/2)]

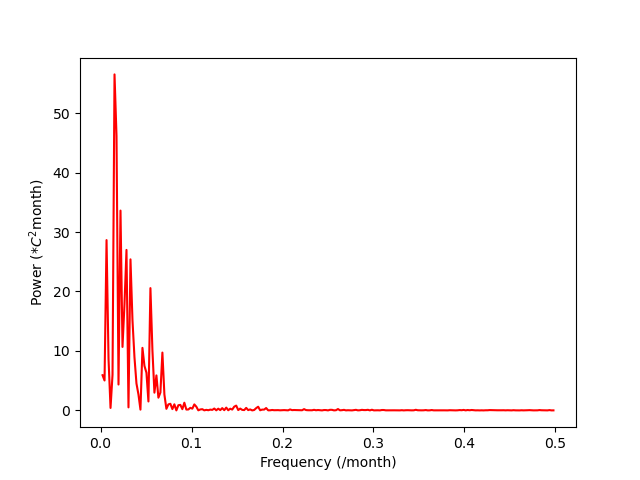
  plt.plot(frequency, power, 'r')
  plt.xlabel("Frequency (/month)")
  plt.ylabel("Power ($*C^2 \mathrm{month}$)")
  plt.show()

  #smoothing
  ave_num = 4

  frequency_mean = np.zeros(int(math.floor(N/2)/ave_num))
  power_mean     = np.zeros(int(math.floor(N/2)/ave_num))

  for nn in range(0, int(math.floor(N/2)/ave_num)):
    frequency_mean[nn] = np.mean(frequency[ave_num * nn: ave_num * (nn + 1) - 1])
    power_mean[nn]     = np.mean(power[    ave_num * nn: ave_num * (nn + 1) - 1])

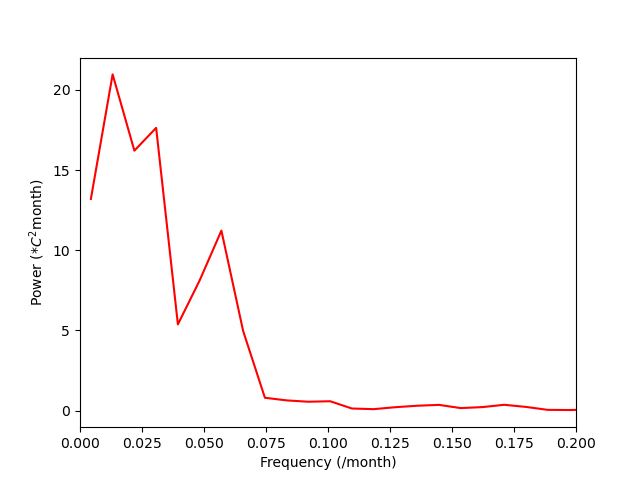
  plt.plot(frequency_mean, power_mean, 'r')
  plt.xlim(0, 0.2)
  plt.xlabel("Frequency (/month)")
  plt.ylabel("Power ($*C^2 \mathrm{month}$)")
  plt.show()