🏃‍♀️

今日からできるプログラムの高速化(C/C++)

2021/07/05に公開

C++

高速化

キャッシュ

tech

これは何？

普段プログラムを書く際に、特別な学習・リソースを特に必要とせずに手軽にできる高速化をまとめました。特別な学習・リソースというのは、時間をかけて並列化技術を学んだり、その他チューニングをめちゃめちゃ頑張ったり、クソ高いGPUを買ったりということです。そういった手間のかかること無しに、ちょっと気をつけるだけで今日からできる高速化を扱います。

言語はC/C++を例にとっていますが、別の言語でもその仕様を理解して読み替えれば適用できるものになっています。特別なライブラリは用いておらず、Linux、Mac、WSLなどのUNIX系環境があればすぐに試すことができます。Windowsのみの人もVisualStudioで同じことができると思います(私は詳しくないので適宜読み替えてください)。

対象読者

普段高速化を余り意識していないけど意識したい方
アルゴリズムの時間計算量は考えるけど実装は割と大味気味な方
手っ取り早く高速化に触れてみたい方

逆に本記事では初歩的な高速化しか扱わないので高速化に慣れている方は得るものが無いかもしれません。

前提知識

C/C++の基本的な知識
コンピュータの動作に関するごく基本的な知識

実行環境

CPU: Intel(R) Core(TM) i7-9700K CPU @ 3.60GHz
RAM: 32GB
OS: Ubuntu 20.04 LTS
コンパイラ: gcc 9.3.0, g++ 9.3.0

1. コンパイラに任せる

コンパイラは偉いので、コードを最適化してくれるオプションが提供されている場合が多いです。例えばgcc/g++では
-O0　最適化しない(do no optimization)。デフォルト。
-O1　最小限の最適化をする(minimally)。
-O2　さらに最適化する(more)。
といったように多段階に分けて提供されています。
例として
定数 $a_0, a_1, a_2$ 及び既知の配列 $x_i (i = 0, 1, ..., n-1)$ から

out_i = a_0 x_i - 2a_1 x_i + a_2 x_i \ \ \ (i = 0, 1, ..., n-1)

を計算する。
という処理をやってみます。

muladd.c

#include <stdio.h>
#include <stdlib.h>
#include <time.h>

void print_elapsed_time(clock_t begin, clock_t end) {
    float elapsed = (float)(end - begin) / CLOCKS_PER_SEC;
    printf("Elapsed Time: %15.7f sec\n", elapsed);
}

int main()
{
    const int num_loop = 65536;
    const int n = 65536;

    volatile const float a0 = (float)rand();
    volatile const float a1 = (float)rand();
    volatile const float a2 = (float)rand();
    float x[n];
    float out[n];
    
    for (int i = 0; i < n; ++i)
        x[i] = (float)rand();
    
    // start to measure
    clock_t begin = clock();
    for (int loop = 0; loop < num_loop; ++loop)
        for (int i = 0; i < n; ++i)
            out[i] = a0 * x[i] - 2 * a1 * x[i] + a2 * x[i];
    clock_t end = clock();
    // end

    // use 'out' to prevent the compiler from ignoring it.
    for (int i = 0; i < n; ++i)
        out[i] += 0.1;  
    print_elapsed_time(begin, end);

    return 0;
}

配列outを計算後に一度も使用しないとコンパイラの最適化で不要と判断されて適切に計算が行われない場合もあるため、念のため時間計測修了後に弄っておきました。
これをgccの各最適化レベルでコンパイルすると、実行時間は以下のようになりました。

option	time [s]
-O0	9.3683090
-O1	4.6673341
-O2	3.0075941

これだけでもかなりの変化です。ただしシーンによってはこういうこともあり得るので気をつけたほうが良さそうです。ちなみに

gcc -S -O0 muladd.c
gcc -S -O2 muladd.c

で出力されるアセンブリソースを比較するといかに最適化されたかを見ることもできます。

以降は-O2を付けて測定します。

2. 括弧でくくり乗算を減らす

1.と同様の計算式を観察してみます。
[括弧でくくらない]

out_i = a_0 x_i - 2a_1 x_i + a_2 x_i \ \ \ (i = 0, 1, ..., n-1)

[括弧でくくる]

out_i = (a_0 - 2a_1 + a_2)x_i \ \ \ (i = 0, 1, ..., n-1)

は等価です。
しかし後に見るように後者の方が計算が速くなります。何故でしょうか。
それは加算(減算)と乗算の回数に関係しています。一般に四則演算の速度は
加算

≒

減算

<

乗算

<

除算
となります(除算の遅さについては後ほど着目します)。といっても加減乗はほとんど同じになる場合が多く、除算は明確な差を持って遅いことが多いです。
演算回数を数えてみましょう。
[括弧でくくらない場合]
加減: 2回
乗: 4回
[括弧でくくる場合]
加減: 2回
乗: 2回
となり、後者の方がコストが小さいことがわかります。

コードはこちら(変更部分のみ)

muladd_2.c

// start to measure
clock_t begin = clock();
for (int loop = 0; loop < num_loop; ++loop)
	for (int i = 0; i < n; ++i)
	    out[i] = (a0 - 2 * a1 + a2) * x[i];
clock_t end = clock();
// end

測定結果は以下のようになりました。

括弧の有無	time [s]
無し	3.0075941
有り	2.3979111

高速化されていますね。
コンパイラによっては最適化でやってくれる場合もありますが、この場合はやってくれませんでした。今回のように浮動小数点演算を含む場合は誤差の問題があるので、例えば科学計算などの場合は誤差を把握した上で自分でやった方が良いですね。

3. 一時変数の活用

forやwhileなどのループにおいて、ループ内に毎回のループで同一の結果となる演算・関数呼出しなどがあれば、それを毎回計算するのはもったいないです。これをループに入る前に予め計算しておき、一時変数に格納しておけば効率が良いです。
2.では係数を括弧でくくることで

out_i = (a_0 - 2a_1 + a_2)x_i \ \ \ (i = 0, 1, ..., n-1)

としましたが、この係数部分

(a_0 - 2a_1 + a_2)

は何度計算しても同じ結果です。
これを一時変数に入れます。

muladd_3.c

float coef = a0 - 2 * a1 + a2;
// start to measure
clock_t begin = clock();
for (int loop = 0; loop < num_loop; ++loop)
	for (int i = 0; i < n; ++i)
	    out[i] = coef * x[i];
clock_t end = clock();
// end

これにより測定結果は次のようになりました。

一時変数	time [s]
無し	2.3979111
有り	1.2682689

かなり高速化されました。

4. 除算を回避する

2.で除算は遅いと述べました。コンパイラが最適化してくれる場合もありますが、できれば自分でやったほうが良いです。
例えばちょっと頭をひねれば

z =　\frac{x-2}{x+1}\frac{y+1}{y^2+1}

は

z = \frac{(x-2)(y+1)}{(x+1)(y^2+1)}

と等価で、除算を2回から1回に減らすことができます。
代わりに乗算が1回増えますが、除算の方が遅いので総じて効率的になります。
ここでは

out_i = \frac{x_i}{coef}

を計算したいと思います。

div_array.c

#include <stdio.h>
#include <stdlib.h>
#include <time.h>

void print_elapsed_time(clock_t begin, clock_t end) {
    float elapsed = (float)(end - begin) / CLOCKS_PER_SEC;
    printf("Elapsed Time: %15.7f sec\n", elapsed);
}

int main()
{
    const int num_loop = 65536;
    const int n = 65536;

    volatile float coef = (float)rand() + 1e-9;
    float x[n];
    float out[n];
    
    for (int i = 0; i < n; ++i) {
        x[i] = (float)rand();
    }
    
    // start to measure
    clock_t begin = clock();
    for (int loop = 0; loop < num_loop; ++loop)
        for (int i = 0; i < n; ++i)
            out[i] = x[i] / coef;
    clock_t end = clock();
    // end

    // use 'out' to prevent the compiler from ignoring it.
    for (int i = 0; i < n; ++i)
        out[i] += 0.1;  
    print_elapsed_time(begin, end);

    return 0;
}

一方で、

invcoef := \frac{1}{coef}

のように

coef

の逆数を予め計算しておき、一時変数に入れておくと除算を回避できます。

div_array_2.c

float invcoef = 1.0 / coef;
// start to measure
clock_t begin = clock();
for (int loop = 0; loop < num_loop; ++loop)
for (int i = 0; i < n; ++i)
    out[i] = invcoef * x[i];
clock_t end = clock();
// end

測定結果はそれぞれ

除算	time [s]
有り	2.7701349
無し	1.2927580

となり、大きく高速化しました。

5. ループアンローリング(Loop Unrolling)

forループでは毎回ループの終了条件の真偽判定、ループ内変数の更新処理を行うため、意外にもオーバーヘッドとなります。
そこで、いくつかのループをひとまとまりにして実行します。そうすることでループ毎の処理の回数が減り、高速化が見込めます。
ここでは二次元配列の総和を計算するプログラムを考えます。

matsum.cpp

#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <vector>

void print_elapsed_time(clock_t begin, clock_t end) {
    float elapsed = (float)(end - begin) / CLOCKS_PER_SEC;
    printf("Elapsed Time: %15.7f sec\n", elapsed);
}

int main()
{
    const int n = 16384;
    std::vector<std::vector<float>> a(n, std::vector<float>(n, 0));
    for (int i = 0; i < n; ++i) {
        for (int j = 0; j < n; ++j) {
            a[i][j] = (float)rand();
        }
    }

    float sum = 0.0f;
    // start measure
    clock_t begin = clock();
    for (int i = 0; i < n; ++i) {
        for (int j = 0; j < n; ++j) {
            sum += a[i][j];
        }
    }
    clock_t end = clock();
    // end

    print_elapsed_time(begin, end);
    
    printf("sum = %f\n", sum);

    return 0;
}

このループ部分を

matsum_2.cpp

float sum = 0.0f;
// start measure
clock_t begin = clock();
for (int i = 0; i < n; i++) {
	for (int j = 0; j < n; j+=4) {
	    sum += a[i][j];
	    sum += a[i][j+1];
	    sum += a[i][j+2];
	    sum += a[i][j+3];
	}
}
clock_t end = clock();
// end

として、4個まとめて実行するようにします。
結果は

unrolling	time [s]
無し	0.5284120
有り	0.3060660

と高速化しました。

6. キャッシュメモリの有効利用

ここでは、5.の二次元配列の総和について、キャッシュを意識した行列の参照順序により高速化したいと思います。

メモリの知識

必要となるメモリの知識について簡単に解説します。
CPUは一般に演算を行う際に、メインメモリ上にあるデータを一度レジスタに移してから実行します。メインメモリもレジスタも、あるいはハードディスクも広く言えば"記憶装置"と言えますが、そのアクセス速度・容量には大きな違いがあります。

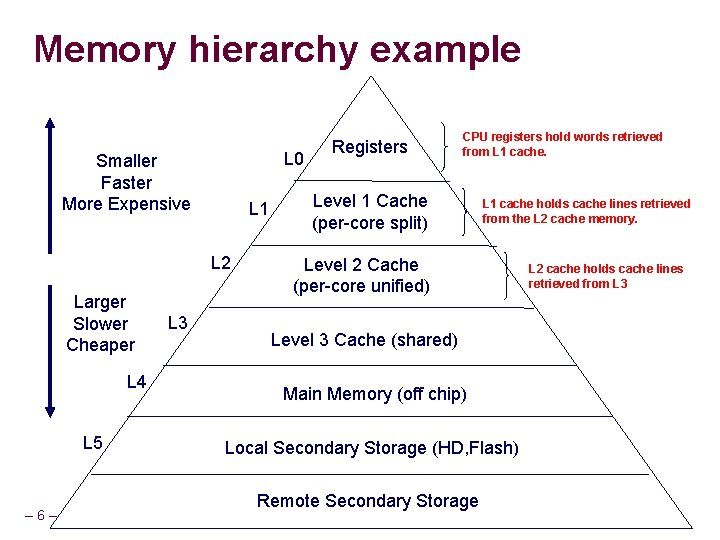
図1 記憶装置の速度と容量 (出典: https://slidetodoc.com/memory-hierarchy-memory-operating-system-and-cpu-memory/)

だいたいレジスタ、(L1~L3)キャッシュ、メインメモリ、HDD/SSDの順で容量は大きくなりますが、その分アクセス速度が低速になります。
レジスタ、キャッシュは一般にCPU内部にあり、メインメモリに比べてアクセスが非常に速いです。先ほどCPUは演算を行う際にメインメモリ上にあるデータを一度レジスタに移すと書きましたが、メインメモリに多数回アクセスすれば処理が遅くなってしまいます。ということで、メインメモリにアクセスする頻度を減らしてキャッシュを利用する、言い換えれば所望のデータがうまくキャッシュ上に載るように工夫することが大切になります。
さらに、キャッシュメモリはメインメモリに比べて容量が非常に小さいです。実際に皆さんの環境で調べてみましょう。ハードウェア情報の確認には例えば

$ lscpu

などのコマンドが使えます。
実行環境に掲載したメインメモリのサイズは32GBですが、CPUのキャッシュサイズは
L1d cache(データ用): 256 KiB
L1i cache(命令用): 256 KiB
L2 cache: 2 MiB
L3 cache: 12 MiB
でした(勿論CPUに依り異なります)。
このキャッシュメモリをうまく活用することが高速化の鍵の1つになります。

キャッシュメモリの活用

次にこのキャッシュメモリをうまく活用する方針を考えます。
データは基本的に

メインメモリ -> レジスタ & キャッシュ -> 演算回路 -> レジスタ & キャッシュ -> メインメモリ

という流れをたどります。レジスタに格納する際に一部キャッシュメモリにも格納するため、そのデータはメインメモリまで取りに行く必要はなく、アクセスが高速になります。キャッシュメモリには、演算で必要なデータとその周辺のデータの一連のまとまり(キャッシュライン)が保存されます。そのため、同じor近傍にあるデータにアクセスするとキャッシュを有効活用できます。具体的にはメモリアクセスをシーケンシャル(連続した順序)にしたり、近傍にあるデータを扱うパートをブロック化してアクセスを局所的にしたり、といったことを行います。
このように要求されたデータがキャッシュにあり、それを取ってこれることをキャッシュヒットと表現します。逆に欲しいデータがキャッシュになく、メインメモリまで取りに行かなければならない状況をキャッシュミスと表現します。要するに、キャッシュミスを減らしてキャッシュヒットする割合を上げるというのが方針になるわけです。

二次元配列の場合の具体例

二次元配列

i \ j	0	1	...	N-1
0	a[0][0]	a[0][1]	...	a[0][N-1]
1	a[1][0]	a[1][1]	...	a[1][N-1]
...	...	...	...	...
N-1	a[N-1][0]	a[N-1][1]	...	a[N-1][N-1]

は、C/C++では、メモリ上では横方向に連続して各要素が配置されています。
(a[0][0], a[0][1], ..., a[0][N-1]の順)
先程述べたように、メモリは連続に・近傍にアクセスする方がキャッシュヒットしやすくなります。もし二次元配列を縦方向にアクセスしたとすると、十分大きい二次元配列の場合はキャッシュミスが多発し効率が悪くなります。

これを検証してみましょう。
横方向にアクセスする場合(再掲)

matsum.cpp

float sum = 0.0f;
// start measure
clock_t begin = clock();
for (int i = 0; i < n; i++) {
	for (int j = 0; j < n; j++) {
	    sum += a[i][j];
	}
}
clock_t end = clock();
// end

縦方向にアクセスする場合

matsum_3.cpp

// start measure
clock_t begin = clock();
for (int i = 0; i < n; i++) {
	for (int j = 0; j < n; j++) {
	    sum += a[j][i];
	}
}
clock_t end = clock();
// end
}

結果は次の通りになりました。

方向	time [s]
横	0.5284120
縦	1.6317400

かなり高速化されています。キャッシュすごい。

まとめ

高速化というとGPU、並列化、そのためのOpenMP,OpenCL,CUDA,...といったワードが思い浮かびます。これらは非常に強力ですが、私のように経験が浅いと初学者のうちはかなり障壁を感じる分野でもあると思います。ですが、今回挙げたような工夫だけでも簡単に高速化できることもあるのです。
この他にも、浮動小数点の精度を必要最低限にしたり、そもそも無駄な計算を省いたり、数学的な考察でアルゴリズムの時間計算量を改善したりという根本的な工夫もあります。
プログラムは基本的に高速な方が嬉しいと思うので、時間計算量の考察の他にも、このような工夫を試してみるのはとても大切だなと感じました。何よりも速度が上がっていくのを見るのはワクワクしますね！

参考資料

[1] http://rakasaka.fc2web.com/delphi/numop.html
[2] https://www.symmetric.co.jp/blog/archives/87
[3] https://slidetodoc.com/memory-hierarchy-memory-operating-system-and-cpu-memory/
[4]北山洋幸著『高速化プログラミング入門』カットシステム, 2016年
[5] Clay Breshears著『並列コンピューティング技法』オライリー・ジャパン, 2009年