Net Benefit
Net Benefitという概念を理解したい。
なお、岡田先生のnoteという最高にわかりやすい記事もある。
実際に使いたい時はパッケージがあるようなので使ってみたい。
→挙動を再現したスクラップが下にある。ここで試したもの以外にもチュートリアルでは色々と記載されているので、また追って確認したい。
Net Benefit とは
Vickers et al. 2016 で説明されている事例としては、次のようなものである。
- ある標準的な検査を行ったとき、そのうち25人が検査陽性で生検を行うことになった実際に疾患のある患者さん(真陽性; true positive)で、75人は検査陽性で生検をされたが実際には疾患を持たない患者さん(偽陽性; false positive)とする。
- ここに新しい検査として、その同じ集団に対して検査を行った場合に、50人しか偽陽性はでないが、22人しか真陽性を補足できないような検査が出てきたとする。この新しい検査では25人の偽陽性を減らしているが3人の真陽性も減らしている。
- このトレードオフを受け入れるかどうかが、この新しい検査を受け入れるかどうかを考える上で重要なポイントである。仮に、1名の真陽性を見つけるために9名の偽陽性があってもよいと考えられるのであれば(この比率をexchange rateという)、標準検査のNet Benefitは25% - 75% * (1/9) = 16.7%、新検査のNet Benefitは22% - 50%*(1/9) = 16.4%と計算され、標準検査の方が臨床的メリットがあると判断される。
肺がん検診のNet Benefitの計算
さて、実際に応用してみたいと思っていたところに河北健診クリニックの2019年度の各種がん健診の検査結果のデータあったので、これを使ってみたい。
例として肺がん検診のデータを使う。
肺がん検診の結果:
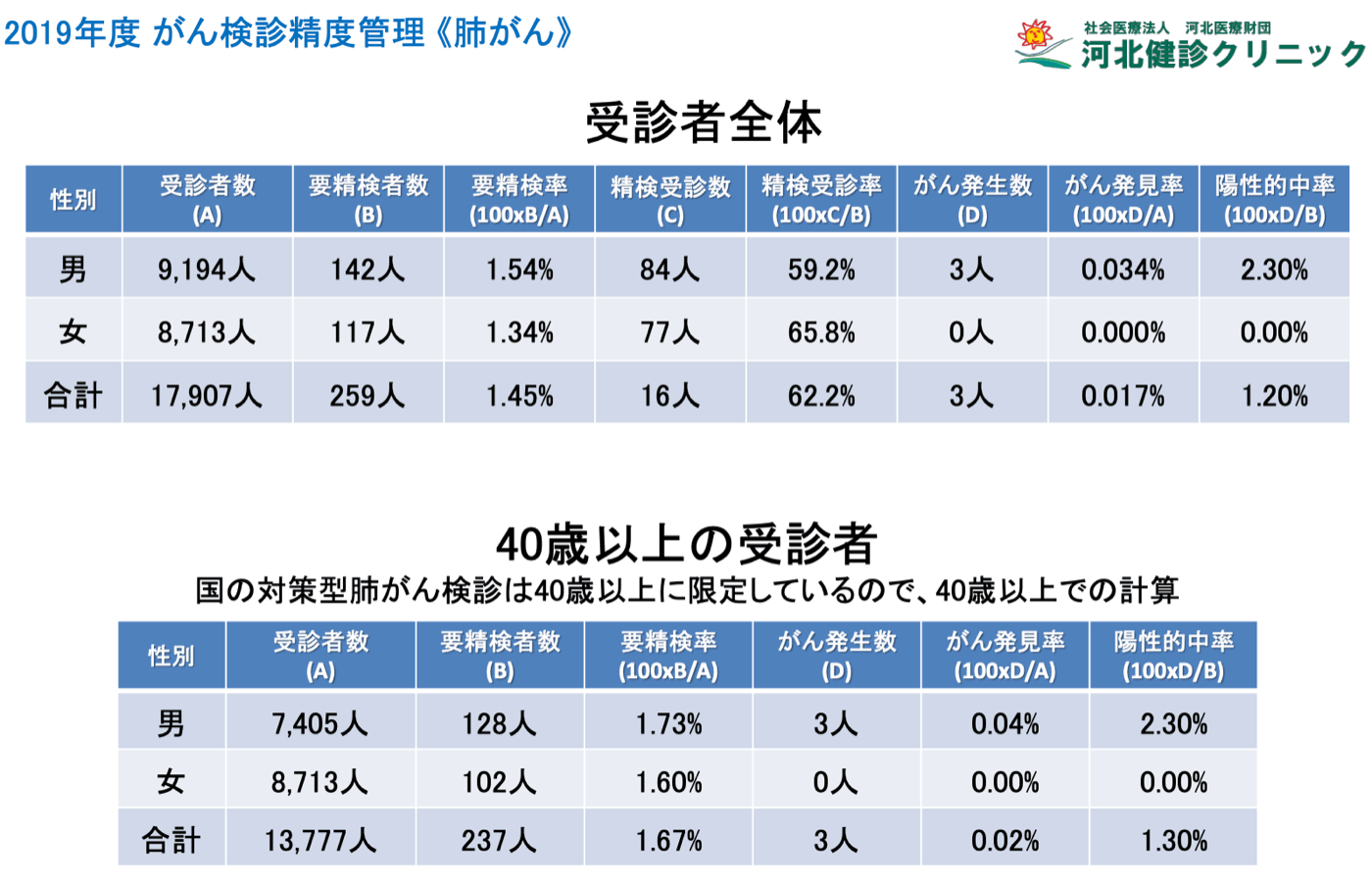
資料に記載のある人口40歳以上における肺がん患者数の期待値:
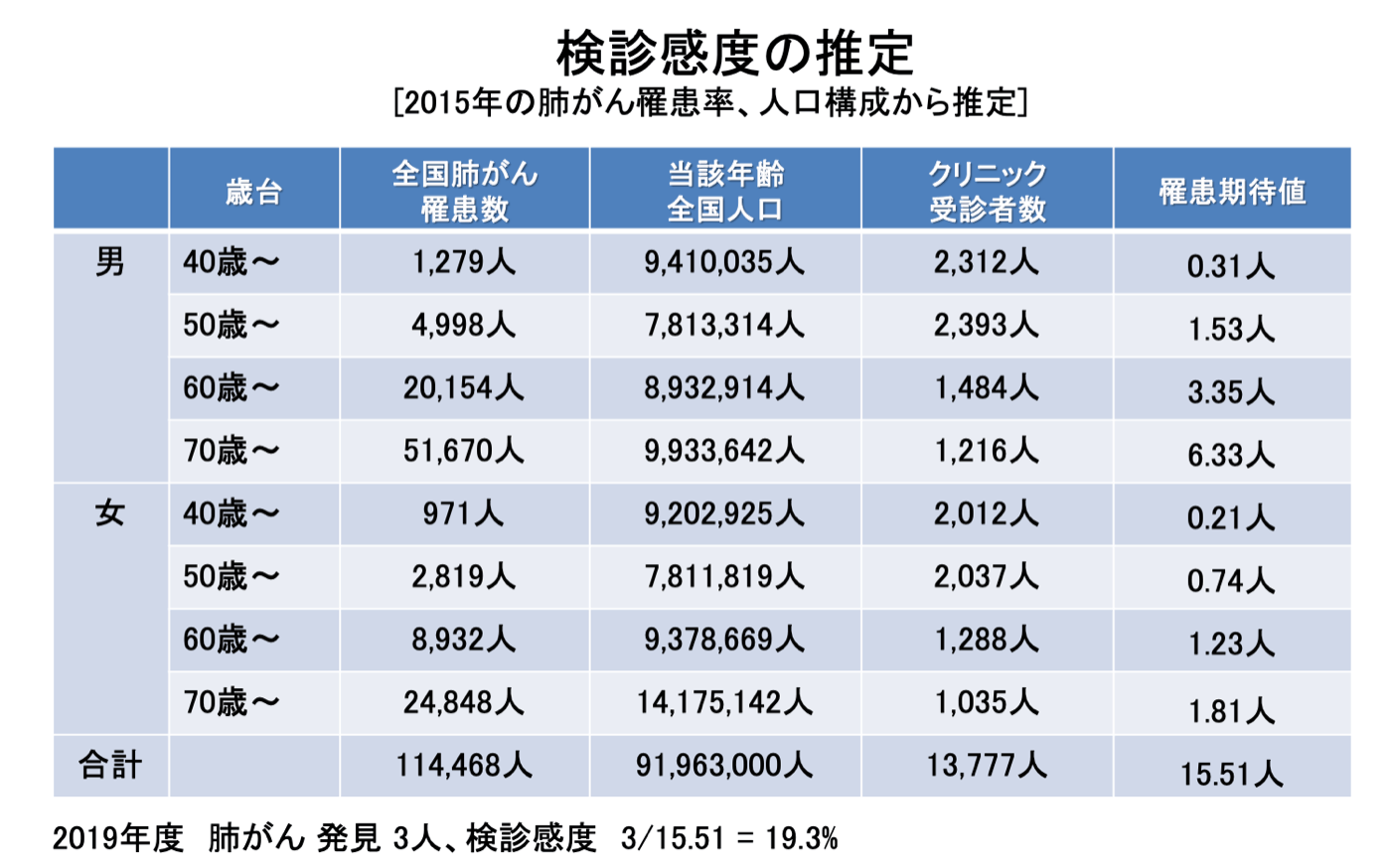
上のデータから2by2を作成する。検査陽性の人数は要検査となった人数を用いた。理患者数は期待値として記載されている数字を用い、端数を切り上げた。

まず、真陽性の割合は3/7421, 偽陽性の割合は125/7421となる。
次に、exchange rateを考える。国策としての肺がん検診の対象40歳以上におけるPPVが1.3%となっているのでこれを約1%とすると、1人の肺がん患者さんを見つけるために、99名の非肺がん患者さん判定が出ることが受け入れられていると解釈できて、exchange rateは1/99になるはず。
N <- 7421
exchange_rate <- 1/99
disease <- 3/N
non_disease <- 1-disease
結果、Net Benefitが0を下回った約-1%だった・・・。
> disease - exchange_rate * non_disease # net benefit
[1] -0.009692668
これ(の計算があっているのかもわからないが)が高いのか低いのかは比較してみないとわからない。40歳以上の肺がん検診を行わない場合と比較ができればいいのだろうか。
当該論文の中のFig1やFig2を見る感じでは、何も検査を行わないケースではNet benefit = 0 ということになっていることを考えると、0を下回るということは検診をする方が臨床的にメリットがないという解釈となると思われる。
異なるexchange rateでのNet Benefitの計算
上の1/99よりは、実は臨床的に受け入れられるexchange rateよりも高い可能性も考えられるので、もっと低いexchange rate(真陽性1名と釣り合う偽陽性がもっと多い)場合まで幅を持たせてNet Benefitを見てみる。exchange rateの下側は10^-5、1人の真陽性に対して99999人の偽陽性を許容する想定とした。結果は、下限付近のexchange rateでかろうじて0を微妙に超える程度だった。ゆえに、40歳以上の肺がん検診を実施することが検診を全く実施しないことに比べて臨床的に意味があるのは、上記exchange rate下限に近いような状況のみに限られると言える。ただ、検診は個人レベルで受けたいと思えば受けられるので、国策として検診を全くしなくても検診を受ける人はいるはずで、本来ならばその辺りも考慮しないといけない気がする。
exchange_rate_range <- seq(0.00001, 0.01, 0.00001)
netb_nefit_range <- disease - exchange_rate_range * non_disease
plot(exchange_rate_range, netb_nefit_range, type = 'l', ylim=c(-0.01,0.01))
abline(a=0, b=0, col = 'red', lty = 'dotted')
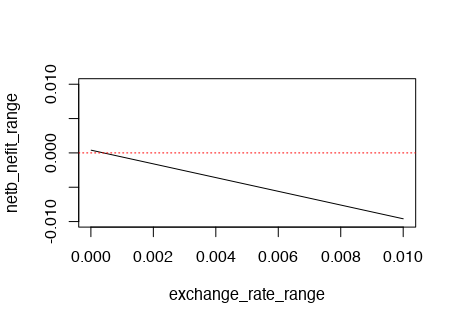
実際、exchange rateをかける前の真陽性/N, 偽陽性/Nの値を見てみると、真陽性/Nがかなり小さかった。
> disease
[1] 0.0004042582 # tp/N
> non_disease
[1] 0.9995957 # fp/N
Decision curve analysis
このようにexchange rateを変えた時のNet Benefitを描くいた図をDecision curveというらしい。今回は検査の閾値設定が不明なので、真陽性・偽陽性を固定のままexchange rateだけ変動させたが、予測モデルなどに用いる場合には少し考え方が異なり、陽性判定をするための閾値をずらしてそれに紐づいてexchange rateも変わっていくようだ。
論文では、「予測モデルなどで陽性判定する閾値を10%とすること」=「10名検査して1名の罹患患者を見つけられる比率がexchaneg rateであること」=「1名の真陽性と9名の偽陽性が釣り合うと考えること」と説明されている。
アウトカムの確率が10%と予測されたら、そのような人を10人集めてようやく1人アウトカムを持っているということなので、1名の真陽性と9名の偽陽性が出るということは分かる。閾値を10%にするということは最大でここまでの真陽性:偽陽性比率を許容するということだから、この比率をexchange rateとして解釈できるということだろうか。
その他
- 上述閾値の解釈を適用するためには予測モデルが予測確率0から1の範囲でwell-calibratedな必要があると思う。
- 患者背景によってもこのexchange rateは変わりえる気がする。実際当該論文の"Choice of threshold probabilities"という章に記載のある医師のコメントも最後の方でその点に触れている。例えば、若年層と高齢者層ではPPVに影響するprevalenceが異なりそうであるし、個々人によって何を好むかは変わりそうである。
-
Vickers et al. 2019のQAセクションも有益。
- 識別と臨床的有用性が乖離するのはどのような時かについての説明:識別はあくまで相対的なもの(推定された確率が高いものと低いものがあった時に実際に推定確率が高い方で疾患を持ち、低い方で疾患を持たないという関係であれば良い)なので、推定確率を全部10で割っても識別力は変わらないが、推定確率が40%の時と4%の時では取り得るアクションは変わってくるだろう。
- P値や信頼区間を使わないのかという質問に対する説明:急いで家に帰りたい時に、バスAは平均30分かかり、バスBは平均35分かかるということがわかっていたとして、母平均または母中央値レベルで違いがあるかどうかに関係なくバスAを使うだろう。
- この話はベイズでP値を使わないという話にも関連する気がする。意思決定に使うという意味では自然なのかな。
{dcurves}のdca()を再現
参考 https://mskcc-epi-bio.github.io/decisioncurveanalysis/dca-tutorial.html
単変数でのDecision Curveをdca()で描く
トイデータをまず作成する。
# Generate a toy dataset
N <- 100
x1 <- rnorm(N)
x2 <- sample(c(0,1), size = N, replace = T)
beta <- c(1,1,0.5)
X <-
matrix(c(rep(1,N), x1, x2),
ncol = 3)
y <- X%*%beta
Y <- unlist(lapply(LaplacesDemon::invlogit(y), rbinom,n=1,size=1))
d <- data.frame(x1,x2,y,Y)
x2のNet Benefitをまず考えようと思う。その前にx2で層別したときのyの密度分布がどうなっているかを確認してみる。beta=0.5とにしているため、あまり識別に寄与していない。
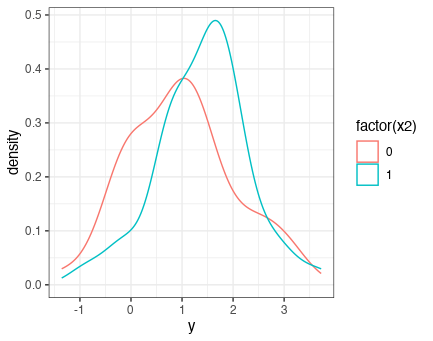
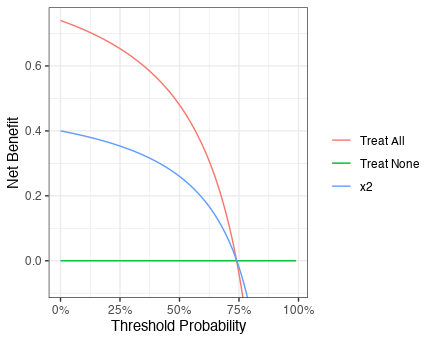
{dcurves}を用いてNet Beneftをプロットしてみる。x2で判断するよりも、全員に介入した方がNet benefitが高いという結果であった。リスクの許容度が高く閾値が75%くらいの時(75:25 = 3:1, i.e., 3人の真陽性でようやく1人の偽陽性を受け入れられるレベル)以降はNet Benefitが0を下回っている。ただし、Decision curveを見てから閾値範囲について考えるのは順序が逆であり、閾値範囲を考えた上でDecision curveを解釈することが正しいので注意。
library(dcurves)
dca(Y ~ x2, data = d) %>% plot()
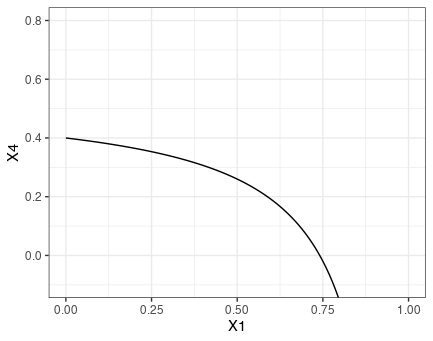
単変数のdca()を再現する
dca()のうちx2=1の時にアウトカムあり、そうでなければなしという場合のNet Benefitの再現を試みる。
increment <- 1000
# when this is 1, exchange_rate -> infinity
iter_range <- seq(0,0.999,1/increment)
nb <- data.frame(matrix(NA,
ncol = 4,
nrow = length(iter_range)))
for(i in 1:(increment)) {
threshold <- iter_range[i]
exchange_rate <- threshold/(1-threshold)
# 2by2 table
# I want to see NB by x2 prediction
tp_rate <- sum(x2*d$Y)/N
fp_rate <- sum(x2*(d$Y==0))/N
nb[i,1] <- threshold
nb[i,2] <- tp_rate
nb[i,3] <- fp_rate
nb[i,4] <- tp_rate - exchange_rate * fp_rate
}
ggplot(nb) +
geom_line(aes(x=X1, y=X4)) +
coord_cartesian(ylim = c(-0.1,0.8)) +
theme_bw()
dca()をするとdcaという名前のtibbleが存在するので、そこから数値一致確認に使うものを取り出す。また、dca()は0.01単位で閾値を動かしているが、自分は0.001単位で動かしていたので欲しい粒度の数字のみを取り出す。
out <- dca(Y ~ x2, data = d)
out_extract<-
data.frame(
threshold = out$dca$threshold[out$dca$label=='x2'],
tp_rate = out$dca$tp_rate[out$dca$label=='x2'],
fp_rate = out$dca$fp_rate[out$dca$label=='x2'],
net_benefit = out$dca$net_benefit[out$dca$label=='x2']
)
nb_match <- nb[seq(1,1000,10),]
Net benefitは完全に一致した。
> all.equal(out_extract$net_benefit, nb_match$X4)
[1] TRUE
多変量ロジスティック回帰の場合のNet benefitを再現する
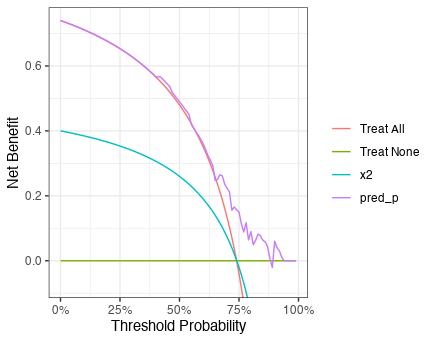
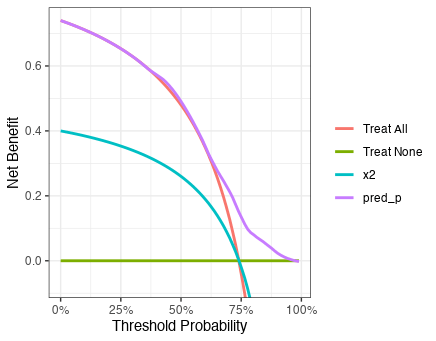
x1とx2を共変量としたロジスティック回帰の予測値のNet Benefitを可視化する。
閾値の高い範囲で予測モデルの方がNet benefitが高いようである。どの範囲であっても予測モデルのNet benefitが他の選択肢と同等あるいは高いので、予測モデルが臨床的に採用されるべき状況と考えられる。
また、予測モデルのNet Benefit曲線は単調増加ではなく増減していることも発見である。
fit <- glm(Y ~ x1 + x2, family = "binomial", data = d)
pred_p <- unname(predict(fit,type = "response"))
d_new <- data.frame(d, pred_p)
dca(Y ~ x2 + pred_p, data = d_new) %>% plot()
上図のうち予測モデルのNet benefit曲線を再現してみる。
increment <- 1000
# when this is 1, exchange_rate -> infinity
iter_range <- seq(0,0.999,1/increment)
nb <- data.frame(matrix(NA,
ncol = 4,
nrow = length(iter_range)))
for(i in 1:(increment)) {
threshold <- iter_range[i]
exchange_rate <- threshold/(1-threshold)
# 2by2 table
# I want to see NB by predicted probability
Y_pred <- as.numeric(d_new$pred_p >= threshold)
tp_rate <- sum(Y_pred*d_new$Y)/N
fp_rate <- sum(Y_pred*(d_new$Y==0))/N
nb[i,1] <- threshold
nb[i,2] <- tp_rate
nb[i,3] <- fp_rate
nb[i,4] <- tp_rate - exchange_rate * fp_rate
}
ggplot(nb) +
geom_line(aes(x=X1, y=X4)) +
coord_cartesian(ylim = c(-0.1,0.8)) +
theme_bw()
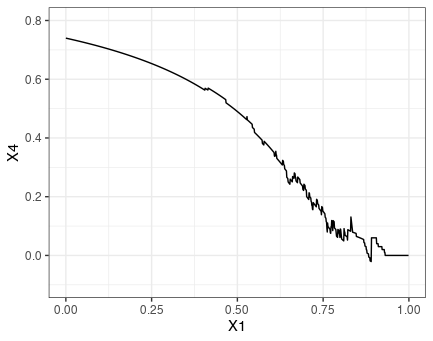
out <- dca(Y ~ x2 + pred_p, data = d_new)
out_extract<-
data.frame(
threshold = out$dca$threshold[out$dca$label=='pred_p'],
pos_rate = out$dca$pos_rate[out$dca$label=='pred_p'],
tp_rate = out$dca$tp_rate[out$dca$label=='pred_p'],
fp_rate = out$dca$fp_rate[out$dca$label=='pred_p'],
harm = out$dca$harm[out$dca$label=='pred_p'],
net_benefit = out$dca$net_benefit[out$dca$label=='pred_p']
)
nb_match <- nb[seq(1,1000,10),]
数値の完全一致を確認した。
> all.equal(out_extract$net_benefit, nb_match$X4)
[1] TRUE
Net benefit曲線の増減部分の調査
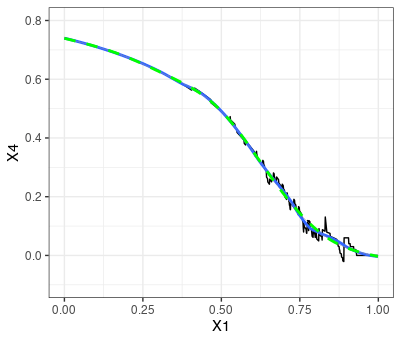
Net Benefitが乱下向している箇所の数値を詳しく見てみる。閾値が0.890の時は0を下回ったNet benefitが閾値が0.891になった際に0.06まで上昇している。
> nb[nb$X1 >= 0.89 & nb$X1 <= 0.891,]
X1 X2 X3 X4
891 0.890 0.06 0.01 -0.02090909
892 0.891 0.06 0.00 0.06000000
どうやら、閾値が0.8903149のに対応しているデータではY = 0だったようだ。よって、閾値が0.890の場合は、このY=0をアウトカムありと判定してしまうため偽陽性が増えるためにNet benefitが減少した。しかし、閾値が0.891の時にはこの症例はアウトカムなしと正しく判定されて真陽性が増えるためにNet benefitが増加した、ということだろう。
> d_new2 <-
+ d_new %>%
+ arrange(pred_p)
>
> d_new2[d_new2$pred_p >= 0.88 & d_new2$pred_p <= 0.91,]
x1 x2 y Y pred_p
92 1.370796 0 2.370796 1 0.8829910
93 1.374301 1 2.874301 1 0.8866992
94 1.485680 0 2.485680 0 0.8903149
95 1.687206 1 3.187206 1 0.9051674
96 1.755040 0 2.755040 1 0.9059263
なお、スムーザーオプションがあるようだ。チュートリアルでも書いているが、スムーザーに加えてスムージングされてない曲線も確認した方が良いだろうが、dca()で両方をoverlayすることはできないぽい。
dca(Y ~ x2 + pred_p, data = d_new) %>% plot(smooth=T)
loessをspan=0.2で使ってみたところ、上図と似たような結果が得られた。natural cubic splinesの自由度6でも曲線を描いてみたが、大体同じような感じであった。自作するとスムージング前後のグラフをoverlayできるなどの柔軟性がある。
ggplot(data = nb,
aes(x=X1, y=X4)) +
geom_line() +
geom_smooth(method='loess', span = 0.2) +
geom_smooth(method = "lm",
formula = y~ns(x,df=6),
col = 'green', linetype = 'dashed') +
coord_cartesian(ylim = c(-0.1,0.8)) +
theme_bw()