Zenn
Open9

NHSTで問題になってベイズ で問題にならないとはどういうことなのか調べる

ironmanironman

ベイズ では問題にならないけれど、Null hypothesis significance testing (NHST)だと問題になるとよく目にする問題について理解を深めたいスクラップ。

ironmanironman

やること: 尤度原理関連の確認

  • 経済セミナー 経済学と再現性問題でマクリン先生が書かれている、二項分布と負の二項分布どちらを想定するかによってP値は異なることを確認する。
  • 尤度を用いる場合には一貫した推論結果になることを確認する。
  • 適当な事前分布をおいて事後分布を確認する。

P値の確認

まず、二項分布を仮定して帰無仮説をp=0.5とした場合のP値を考える。該当記事では正確な片側のP値を出していると思う。なんとなく両側でも計算してみた。

# setting
x <- 3 # 成功
n <- 12 # ベルヌーイ試行回数

# exact two-sided p value from binomial distribution 
pval_lower <- sum(dbinom(0:x, size = n, prob = 0.5))
pval_upper <- sum(dbinom((x+1):n, size = n, prob = 0.5)[dbinom((x+1):n, size = n, prob = 0.5)<=dbinom(x, size = n, prob = 0.5)])

片側の方は該当文献の記載と一致。

> pval_lower
[1] 0.07299805
> sum(pval_lower, pval_upper)
[1] 0.1459961

負の二項分布についても計算してみる。
dnbinom()の引数を理解するのにてこずった。失敗回数を横軸に取ってその確率質量関数を描くイメージを持つと、失敗回数が増える方がより極端なことが起こる方向ということになるのでこの方向が上側P値に対応すると考える。二項分布の試行回数のように上限がないので適当に100回まで失敗するという有り得なそうな数字を使った。

# exact two-sided p value from negative binomial distribution
## 100 is arbitrary
pval_upper <- sum(dnbinom((n-x):100, size = x, prob = 0.5))
pval_lower <- dnbinom(0:(n-x-1), size = x, prob = 0.5)[dnbinom(0:(n-x-1), size = x, prob = 0.5)<=dnbinom(n-x, size = x, prob = 0.5)]

こちらも該当文献の記載と一致。3回の成功を得るまでの失敗回数を減らしていく方向では、1つ目の片側の確率と同程度かそれ以下の確率となる範囲がなかったので、両側が片側と一致した（あってるのか？）。

> pval_upper
[1] 0.03271484
> sum(pval_lower, pval_upper)
[1] 0.03271484

尤度関数の確認

12回中3回成功するベルヌーイ施行を二項分布で考えた時の尤度関数は：

L(\theta; データ) = \binom{12}{3} \theta^3 (1 - \theta)^{9}

で、3回成功するまでに9回失敗した負の二項分布で考えた場合は：

L(\theta; データ) = \binom{11}{2} \theta^3 (1 - \theta)^9

となる。\thetaに関する部分はどちらの尤度関数でも共通しているので、尤度を用いた推論では結果は一致することがわかる。

ベイズ での結果の確認

Beta(a,b)を事前分布とすると、採用した統計モデルが二項分布であろうと負の二項分布であろうと尤度は同じなので事後分布はBeta(x+a, n-x+b)で表現できる。

ベイズだと帰無仮説を考えたりしていないので頻度論と同じP値なるものは多分計算できないと思うのでなんとなく事後分布を図示してみる。

plot(seq(0,1,0.01),
     dbeta(seq(0,1,0.01), shape1 = a+x, shape2 = b+n-x),
     type = 'l',
     xlab = 'theta',
     ylab = 'density')
abline(v = 0.5, col = 'red')

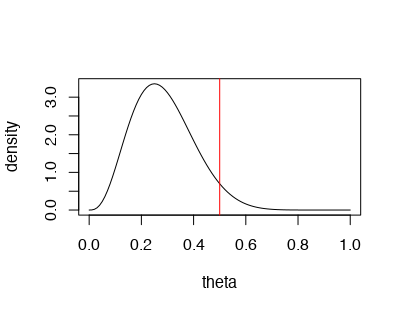
posterior beta dist

パーセンタイルベースの95%信用区間は0.5を微妙に含んでいる。

> qbeta(c(0.025,0.975),shape1 = a+x, shape2 = b+n-x)
[1] 0.09092039 0.53813154

なんちゃって95%HDIを計算してみても同じような区間を得た。

> # 95% highest density interval
> data.frame(
+   p = seq(0,1,0.01),
+   dens, 
+   frac = dens/sum(dens)
+   ) %>%
+   arrange(desc(frac)) %>%
+   mutate(cumfrac = cumsum(frac)) %>% 
+   mutate(
+     intvl95 = ifelse(cumfrac/max(cumfrac)<=0.95,1,0)
+          ) %>% 
+   filter(intvl95==1) %>% 
+   summarise(HDI_lower = min(p), 
+             HDI_upper = max(p))
  HDI_lower HDI_upper
1      0.11      0.52

とはいえ、信用区間に含まれているかどうかという考え方自体が検定的な考え方で良くないだろうし、事後分布を見る限り\theta=0である可能性は低そう。実際、\thetaが0.5以下である事後確率は95%なので、ほぼほぼ0.5より小さいんだろうなという結果と解釈して良さそう。

> pbeta(0.5,shape1 = a+x, shape2 = b+n-x)
[1] 0.9538574

まとめ

  • P値を計算する時に仮定する確率分布が二項分布か負の二項分布かによって（データの取り方によって）P値は異なる。
  • 一方、尤度はどちらの分布を仮定しても同じなので、尤度を使った推論ならば同じ結果を得られる。
  • ベイズ 推論は尤度と事前分布を用いるので、尤度が変わらなければ、同じ事前分布を用いれば同じ推論結果を得られる。

補足

  • 統計的推論に必要な情報が尤度関数に全て含まれるべきという規範のことを尤度原理(Likelihood Principle)というらしい。

今後調べたいこと・気になること

  • 尤度原理とはなんじゃらほい。
  • P値は尤度原理に反しているという記述が当該記事にあるのだけれど、これは尤度比検定のような尤度を用いる検定にも当てはまるのか？
  • 尤度関数がデータの取り方に依存しないというのは常に正しいのか？二項分布と負の二項分布ではそうだったけれど、そうならない場合はないのか？
    • 恐らく、exchangeabilityと関係があると思う。今回の例で言うと、成功と失敗の順列がどうであっても、12回の独立なベルヌーイ試行のうち成功3回・失敗9回という事象を得る確率は変わらないということ。選択的停止の問題も同じで、100例組み入れて30例で効果があった試験と、50組入れて20例に効果があったことを確認してからもう50例を集めて10例に効果があった試験は同じ情報を持っていると考えられるということ（ちゃんとしたRCTならば）、だと思う。
  • exchangeabilityもあまり腑に落ちない概念の一つなのでなんとかしたい。イメージ的なものはこのページとかが良い。証明もちゃんと理解したいけど・・・標準ベイズ にも書いてあったし・・・。けどこのスクラップでは手に余ると思われる。
  • 多重比較がベイズなら問題ならないという話も気になるのだけれど、Gelman先生のブログをチラ見する限りだとこれは事前分布によるshrinkageの効果によるところな気がするので尤度原理とは違う話なのかも？
ironmanironman

Multiple data looksが頻度論に影響を与えるがベイズ に影響を与えないことの感覚的な理解を深めたい

頻度論的な考え方だとデータの集め方（結果を見る→データを集めるを繰り返すこと）に影響を受ける点について、感覚的な説明がHarrell先生のサイトに書いてあった。

Imagine that the military has developed a pattern recognition algorithm to determine whether a distant object is a tank. Initially an image results in an 0.8 probability of the object being a tank. The object moves closer and some fog clears. The probability is now 0.9, and the 0.8 has become completely irrelevant.

遠方から何かが近づいてくる時、それが戦車かどうかを判断する場面。その何かが近づいてくるほど情報が新たに得られているので、だんだんとデータが増えているような状況と考えられる。尤度原理に即したベイズ 統計の場合、例えば100mの距離で戦車である確率が80%で、50mの距離でその確率が90%と計算されたとき、その90%という確率は100m時点で確率が80%であったことから何も情報を得ていない。

これはすんなり理解できそう。頻度論の方はどうだろう。

Contrast with a frequentist way of thinking: Of all the times a tested object wasn’t a tank, the probability of acquiring tank-like image characteristics at some point grows with the number of images acquired. The frequency of image acquisition (data looks) and the image sampling design alter the probability of finding a tank-like image.

うーん、直訳的に読んでいてもちょっとよく分からない。
遠方から近づいてくる物体が戦車ではないと仮定した上でその逸脱度合いを確認することを繰り返していくとき、戦車が近づいてきてその判断を繰り返すごとにその物体が戦車ではないという帰無仮説の仮定の確からしさが変わってしまう、という風に解釈していいだろうか。データが変わればP値を計算するのに用いられる標本分布が変わってしまうことに対応するような気がする。

--

記事の下の方にあるシミュレーションの手順を示した記載で、もう一つ重要だと感じたのがここ。

In the next step it is seen that the Bayesian does not consider a stream of identical trials but instead (and only when studying performance of Bayesian operating characteristics) considers a stream of trials with different efficacies of treatment, by drawing a single value of μ from the prior distribution.

ベイズの場合、1つ1つのデータ点を別のものだと考えている一方、頻度論の場合は全てが同じもの(ある真の母集団)から来ていると考えているという違いだと理解した。つまり頻度論の場合、求めたいものがある母集団から来ているという制約があってそれが推論を歪めているという感じなのではと思った。データ上の相関を考慮せずに解析してeffective sample sizeが小さくなるという話の逆バージョンみたいなイメージ。どうだろう。

--

"Calibration of Posterior Mean at Stopping for Efficacy"という章の図を自分で再現してみるのは良さそう。Harrell先生の記事ではよくbayes is well-calibratedという記載があってどういうことだろうと思っていたけど、このcalibration plotを見て意図が分かった。