EPVとロジスティック回帰のパフォーマンスのシミュレーション
ゴール
- ロジスティック回帰でモデルに投入する変数の数を検討するためのシミュレーションコードを作成する
やること
- van Smeden, M., de Groot, J.A., Moons, K.G. et al. No rationale for 1 variable per 10 events criterion for binary logistic regression analysis. BMC Med Res Methodol 16, 163 (2016). https://doi.org/10.1186/s12874-016-0267-3 のFigureを再現する
- 目的変数の割合を自由に設定できる、色々なデータセットを想定できる、といった拡張性を持たせられる関数を作る
切片を調整することで意図した目的変数の割合になるようなデータを生成する関数
まず、アウトカムの割合を自由に設定した上で、真の対数オッズ比も好きなように設定できるようなデータセットの作成方法を考える。
- 一番安直な方法として、切片を調整する関数を作成することにした。以下は、意図したアウトカムの発現割合になるような切片を推定する関数である。
- 目的変数の割合
y_true_propとパラメータの数P、それから真の対数オッズ比true_betaを指定して、共変量生成の分布のパラメータを与えることで実行できる。 - 今回は切片も込みでパラメータの数をPとした。未来の自分がP-1とPをごっちゃにして苦労する気がしたので、丁寧に
stop()なども記述した(メッセージに具体性がないがきっと分かるだろう)。 - 共変量の分布は「全て正規分布」か「全て二項分布」のパターンしか考慮できていない。共変量の分布の指定に用いるパラメータが与えられていないときには標準正規分布を用いるようにした。
-
optim()のところは、データ生成過程の真の切片をちゃんと推定したいのでNを大きく設定してある。 - ロジットスケールでリニアな関係を真と考えるシミュレーションを想定(ロジットスケールのモデルに二乗項や交互作用などがない)している。
sim_intercept <-
function(N, P, y_true_prop, true_beta,
x_mean=NULL, x_cov=NULL, bin_p=NULL) {
# parameters -----------
# N: sample size
# P: number of coefficients including intercept
# y_true_prop: true y proportion
# x_mean: mean vector of (P-1)
# x_cov: vcov (P-1)*(P-1)
# bin_p: binomial proportion vector of (P-1)
if(!is.null(x_mean) && !is.null(x_cov) &&
length(x_mean) == (P-1) && sum(dim(x_cov)) == 2*(P-1)) {
X_true <- MASS::mvrnorm(n=N, mu=x_mean, Sigma=x_cov)
} else if (!is.null(x_mean) && !is.null(x_cov) &&
any(length(x_mean) != (P-1), sum(dim(x_cov)) != 2*(P-1))) {
stop('specify x_mean and x_cov correctly.')
} else if(!is.null(bin_p) && length(bin_p) == (P-1)) {
X_true <- matrix(NA, nrow = N, ncol = P-1)
for(j in 1:(P-1)) {
X_true[,j] <- rbinom(N, size = 1, prob = bin_p[j])
X_true <- cbind(X_true)
}
} else if(!is.null(bin_p) && length(bin_p) != (P-1)) {
stop('specify bin_p correctly.')
}
# optimization function -------------
foo <- function(b0) {
true_beta <- c(b0,true_beta)
eta <- cbind(rep(1,N),X_true)%*%true_beta
invlogit_eta <- invlogit(eta)
return((mean(invlogit_eta) - y_true_prop)^2)
}
# optimization ---------------
# 追記: fnscaleを小さくする方が、悪い状況下でもマシなシミュレーションをしてくれる
# 今回の論文の再現に用いるパラメータの範囲では問題はなかったが、
# fittingがうまくいかない場合などはこの関数の切片の推定が不良である可能性がある
# ただし、fnscaleを小さくするとその分時間はかかるようになる
o <- optim(0, foo, method="L-BFGS-B", control = list(maxit = 100000, fnscale = 1))
b0 <- o$par
return(b0)
}
標準正規分布の共分散行列生成を生成する関数
今回再現する論文の図は標準正規分布しか使わないので、一旦これだけ関数化しておく。
stdnorm_vcov <-
function(P) {
x_cov <- matrix(0, nrow = P, ncol = P)
diag(x_cov) <- 1
return(x_cov)
}
シミュレーション用の関数
次に、上の関数で得られた切片も与えながら、バイアスやら被覆確率やらを計算するシミュレーション関数を作成する。将来の自分に向けて、忘れそうだけど大事なことをメモしておく。
-
true_beta_inputは要素1の値を入れる。そうするとP-1個の共変量は全て同じ対数オッズ比が真の値という設定になる。一方で、共変量ごとに変えたいときはtrue_beta_input_specify_allに対してベクトルとして与える(要素1つの設定は本来いらなかったかも・・・)。 -
b0には、上の関数で推定された切片の値を与える。 -
x_mean、x_cov、bin_pには、上の切片を推定する関数に与えたものと同じものを与えること。指定しない場合には切片推定関数と同様に標準正規分布が使われる。上の関数とデータ生成に用いるモデルを揃えないと切片がおかしくなるので注意。 -
output_summaryは得られた推定値に対してsummary()を実行した結果も欲しい場合にTRUEにする。 -
output_rawは得られた推定値自体を全て入手したい場合にTRUEにする。ただし、iterationの数を増やしてかつNが大きくなったりするとすごく重くなりそうなので、一旦5000回以上のシミュレーションを回すときはoutput_raw=TRUEにするとストップするようにしてある。 - 分離が起きた場合や収束しなかった場合にはNAとなるように設定してある。ただ、NAとなった回数も出力されるようになっている。
- そして、今後のシミュレーションコード作成のために、(コードの中にもあえてコメントアウトして残してあるが)、
colSums((mat_lwr <= true_beta) & (mat_upr >= true_beta))/iterではうまく被覆確率を計算できなかったことを覚えておくこと (なぜなのかがイマイチよくわかっていない)。iteration1回ごとに被覆されているかの0/1を判断する場合には問題ないが、今回のように結果を得られてからまとめて計算しようとするとうまくいかない。検出力/アルファエラーも同様である。 - それぞれの変数が1増えるまたはON/OFFされた場合のリスク比やリスク差も出力するようにしているので、オッズ比の大きさをいじりつつも、実際どのくらいの大きさのリスク因子に相当するのかを考えられるようにしているのはポイントの一つ。
- それ以外に何が出力されるかはself-explanatoryなはずなので説明しない。
run_simulation <- function(N, true_prop, P, true_beta_input=NULL,
true_beta_input_specify_all = NULL, b0,
iter = 10, x_mean = NULL, x_cov = NULL,
bin_p = NULL,
output_summary = FALSE,
output_raw = FALSE) {
if(iter>=5000 && output_raw) {
stop('The output object is likely to be too large.')
}
if (length(true_beta_input) == 0 & length(true_beta_input_specify_all) == 0) {
stop('Specify either true_beta_input or true_beta_input_specify_all')
} else if (length(true_beta_input) != 0) {
true_beta <- rep(true_beta_input, P-1)
} else if (length(true_beta_input_specify_all) != 0) {
true_beta <- true_beta_input_specify_all
}
# Set up parameters
# default X matrix is multivariate standard normal
if (is.null(x_mean) && is.null(bin_p)) {
x_mean <- rep(0, P-1)
}
if (is.null(x_cov) && is.null(bin_p)) {
x_cov <- stdnorm_vcov(P-1)
}
true_beta_int <- c(b0, true_beta)
# Initialize results storage
result_beta <- list()
result_bias <- list()
result_lwr <- list()
result_upr <- list()
fitting_success <- logical(iter)
# Iteration
for(i in 1:iter) {
if(!is.null(x_mean) && !is.null(x_cov) && is.null(bin_p)) {
# Multivariate normal
X_true <- rmvn(N, x_mean, x_cov)
} else if(!is.null(bin_p)) {
# independent binomial
X_true <- matrix(NA, nrow = N, ncol = P-1)
for(j in 1:(P-1)) {
X_true[,j] <- rbinom(N, size = 1, prob = bin_p[j])
X_true <- cbind(X_true)
}
}
eta <- cbind(rep(1, N), X_true) %*% true_beta_int
invlogit_eta <- LaplacesDemon::invlogit(eta)
y <- unlist(lapply(as.vector(invlogit_eta), FUN = rbinom, n = 1, size = 1))
dat <- data.frame(X_true, y)
colnames(dat) <- c(paste0('X', 1:(P-1)), 'Y')
fit <- tryCatch({
glm(Y ~ ., data = dat, family = binomial())
}, warning = function(w) {
message("Warning: ", conditionMessage(w))
NULL
}, error = function(e) {
message("Error: ", conditionMessage(e))
NULL
})
if (!is.null(fit) && fit$converged) {
fitting_success[i] <- TRUE
result_beta[[i]] <- coef(fit)[-1]
ses <- sqrt(diag(vcov(fit)))
result_lwr[[i]] <- coef(fit)[-1] - qnorm(0.975) * ses[-1]
result_upr[[i]] <- coef(fit)[-1] + qnorm(0.975) * ses[-1]
result_bias[[i]] <- coef(fit)[-1] - true_beta
} else {
fitting_success[i] <- FALSE
result_beta[[i]] <- setNames(rep(NA, length(true_beta)), paste0("X", 1:(P-1)))
result_lwr[[i]] <- setNames(rep(NA, length(true_beta)), paste0("X", 1:(P-1)))
result_upr[[i]] <- setNames(rep(NA, length(true_beta)), paste0("X", 1:(P-1)))
result_bias[[i]] <- setNames(rep(NA, length(true_beta)), paste0("X", 1:(P-1)))
}
}
# Dataframes of results
mat_coef <- as.matrix(bind_rows(result_beta), ncol = P-1, byrow = TRUE)
mat_bias <- as.matrix(bind_rows(result_bias), ncol = P-1, byrow = TRUE)
mat_lwr <- as.matrix(bind_rows(result_lwr), ncol = P-1, byrow = TRUE)
mat_upr <- as.matrix(bind_rows(result_upr), ncol = P-1, byrow = TRUE)
# Coverage probability
lwr_bool <- matrix(apply(mat_lwr, MARGIN = 1, function(x) x <= true_beta), ncol = P-1)
colnames(lwr_bool) <- colnames(mat_lwr)
upr_bool <-matrix(apply(mat_upr, MARGIN = 1, function(x) x >= true_beta), ncol = P-1)
colnames(upr_bool) <- colnames(mat_upr)
coverage <- colSums(lwr_bool & upr_bool, na.rm = T)/iter
## this does not work
## colSums((mat_lwr <= true_beta) & (mat_upr >= true_beta))/iter
# Power / Alpha error
lwr_bool_power <- matrix(apply(mat_lwr, MARGIN = 1, function(x) x >= 0), ncol = P-1, byrow=T)
colnames(lwr_bool_power) <- colnames(mat_lwr)
upr_bool_power <- matrix(apply(mat_upr, MARGIN = 1, function(x) x <= 0), ncol = P-1, byrow=T)
colnames(upr_bool_power) <- colnames(mat_upr)
power_alpha_error <- colSums(lwr_bool_power | upr_bool_power, na.rm = T)/iter
# risks
(r0 <- invlogit(true_beta_int[1]))
(r1 <- invlogit(true_beta_int[1] + true_beta_int[2:P]))
# Summarize results
summary_stats <- list(
coef_means = colMeans(mat_coef, na.rm = TRUE),
coef_lwr = apply(mat_coef, MARGIN = 2, FUN = quantile, prob = 0.025, na.rm = TRUE),
coef_upr = apply(mat_coef, MARGIN = 2, FUN = quantile, prob = 0.975, na.rm = TRUE),
coverage_prob = coverage,
mean_ci_width = colMeans(abs(mat_upr - mat_lwr), na.rm = TRUE),
bias_means = colMeans(mat_bias, na.rm = TRUE),
relative_bias = colMeans(mat_bias, na.rm = TRUE) / true_beta,
power_alpha_error = power_alpha_error,
rd = r1-r0,
rr = r1/r0,
true_y_prop = true_prop,
epv = N*true_prop/(P-1),
N = N,
P = P,
true_beta = true_beta,
fitting_success = sum(fitting_success)/iter,
covariate = paste0('X', 1:(P-1))
)
if(output_summary&&output_raw) {
out_objects <- list(summary_stats,
coef_summary = summary(mat_coef),
coef_raw = mat_coef)
} else if (output_summary) {
out_objects <- list(summary_stats,
coef_summary = summary(mat_coef)
)
} else if (output_raw) {
out_objects <- list(summary_stats,
coef_raw = mat_coef
)
} else {
out_objects <- summary_stats
}
return(out_objects)
}
1つのシナリオに対するシミュレーションの実行
ある一つのシナリオでシミュレーションを実行するときはこんな感じで使う。複数の共変量があってもlong formatでうまくデータフレームにすることができる点が個人的によかったなと思っている。
P <- 3
true_prop <- 0.5
true_beta <- c(log(1/4),0)
N <- 100
x_mean <- rep(0, P-1)
x_cov <- stdnorm_vcov(P-1)
# Get intercept
b0 <- sim_intercept(N = 100000, P = P, y_true_prop = true_prop,
true_beta = true_beta,
x_mean = x_mean, x_cov = x_cov)
# Run simulation
result <- run_simulation(iter = 100, N = N, true_prop = true_prop, P = P,
true_beta_input_specify_all = c(log(1/4),0), b0 = b0,
output_summary = T,
output_raw = F,
x_mean = x_mean,
x_cov = x_cov)
print(result)
[[1]]
[[1]]$coef_means
X1 X2
-1.43330325 -0.02100322
[[1]]$coef_lwr
X1 X2
-2.1600934 -0.4596002
[[1]]$coef_upr
X1 X2
-0.9226343 0.4203585
[[1]]$coverage_prob
X1 X2
0.98 0.97
[[1]]$mean_ci_width
X1 X2
1.2899490 0.9578935
[[1]]$bias_means
X1 X2
-0.04700889 -0.02100322
[[1]]$relative_bias
X1 X2
0.03390975 -Inf
[[1]]$power_alpha_error
X1 X2
1.00 0.03
[[1]]$rd
[1] -0.299856 0.000000
[[1]]$rr
[1] 0.3998083 1.0000000
[[1]]$true_y_prop
[1] 0.5
[[1]]$epv
[1] 25
[[1]]$N
[1] 100
[[1]]$P
[1] 3
[[1]]$true_beta
[1] -1.386294 0.000000
[[1]]$fitting_success
[1] 1
[[1]]$covariate
[1] "X1" "X2"
$coef_summary
X1 X2
Min. :-2.380 Min. :-0.6938
1st Qu.:-1.668 1st Qu.:-0.1833
Median :-1.351 Median :-0.0102
Mean :-1.433 Mean :-0.0210
3rd Qu.:-1.179 3rd Qu.: 0.1411
Max. :-0.864 Max. : 0.6505
複数のシナリオでのシミュレーション実行
例の文献の図の再現に移る前に簡単なコードの説明。
今回のシミュレーション関数にはforループを使ってしまっているので、少しでも早くなるように{future}と{furrr}を活用している。単純なpmap()と比べると1/4くらいの実行時間にはなった。使い方は簡単で、並列化したいタスクの前にplan(multisession)を実行すればよいらしい。並列化のシャットダウン的なものが他の関数だと必要だがこれは要らないらしい(by chatGPT)。詳しい使い方はぐぐろう。furrr::future_pmap()の使い方はpmap()と同じである。
下記のコードをiter = 10^4で実行すると40分くらいかかるので、iter=1000くらいが短くてかつそれなりの結果が得られるので初手としてはおすすめである。
下記コードのシナリオのパラメータは、論文のFig2 (Study Ia)を再現するためのものである。
n_varying <- seq(30, 300, by = 5)
true_beta_list <- log(c(1/4, 1/2, 1, 2, 4))
P_vec <- 2 # including intercept
varying_inputs <-
expand_grid(P = P_vec, true_beta_input = true_beta_list, N = n_varying) %>%
mutate(true_prop= 0.5) %>%
mutate(epv = N*true_prop/(P-1)) %>%
filter(epv >= 15 & epv <= 150 & (epv%%5)==0)
b0 <-
varying_inputs %>%
pmap(~sim_intercept(N = 100000, P = ..1, y_true_prop = ..4,
true_beta = rep(..2, ..1-1),
x_mean = rep(0, ..1-1), x_cov = stdnorm_vcov(..1))
)
varying_inputs_w_b0 <- data.frame(varying_inputs, b0 = unlist(b0))
# Set up parallel backend ({future})
plan(multisession) # Safe choice, works on all platforms including macOS
system.time(
out <-
varying_inputs_w_b0 %>%
furrr::future_pmap(~run_simulation(iter = 10^4, N = ..3, true_prop = ..4,
P = ..1, true_beta_input = ..2, b0 = ..6,
output_summary = F,
output_raw = F,
x_mean = rep(0, ..1-1),
x_cov = stdnorm_vcov(..1)),
.options=furrr_options(seed = TRUE))
)
再現結果
論文の図で再現できたのは、Study Ia、Ib, Icまでで、IIaは与える条件の説明が不足していて再現がうまくできなかった。
コード自体は大体同じなので、Study Iaの左上のバイアスプロットのグラフ化コードだけ貼っておく。
out_wide <-
out %>%
bind_rows() %>%
mutate(true_beta_cat = paste0('log(',exp(true_beta),')')
)
legendname <- 'True Beta'
out_wide %>%
ggplot() +
geom_point(aes(x = epv, y = bias_means,
col = true_beta_cat,
shape = true_beta_cat,
group = true_beta_cat)) +
geom_line(aes(x = epv, y = bias_means,
col = true_beta_cat,
linetype = true_beta_cat,
group = true_beta_cat)) +
theme_bw() +
labs(x = 'EPV', y = 'Bias',
color = legendname,
shape = legendname,
linetype = legendname) +
theme(legend.title = element_text(size = 10)) +
scale_x_continuous(breaks = seq(min(out_wide$epv), max(out_wide$epv), by = 15)) + # Customize x-axis ticks
scale_y_continuous(limits = c(-0.3, 0.3), breaks = seq(-0.3, 0.3, by = 0.1),
labels = scales::label_number()) # Set y-axis limits and breaks) # Customize y-axis ticks

アウトカム発現割合:1/2
モデルに含まれる共変量の数:1
共変量の分布:標準正規分布
真のオッズ比:1/4, 1/2, 1, 2, 4
N:30から300

アウトカム発現割合:1/2
モデルに含まれる共変量の数:1
共変量の分布:標準正規分布
真のオッズ比:1/4, 1/2, 1, 2, 4
N:30から300

アウトカム発現割合:1/2
モデルに含まれる共変量の数:2, 3, 4
共変量の分布:標準正規分布
真のオッズ比:2, 4
N:60から1200

アウトカム発現割合:1/2,1/3,1/4,1/5,1/10
モデルに含まれる共変量の数:2
共変量の分布:標準正規分布
真のオッズ比:2
N:24から600
自作関数で出せるそのほかの結果
論文には記載がないが、出力できるようにしていた数値をグラフ化したものを貼っておく。
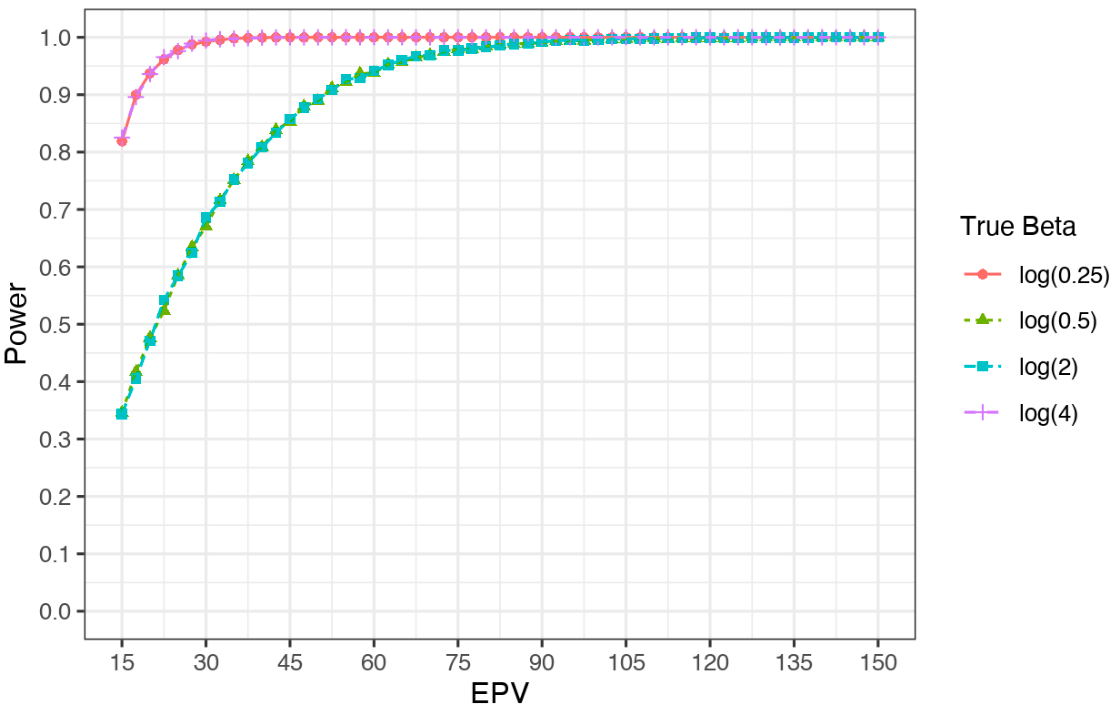
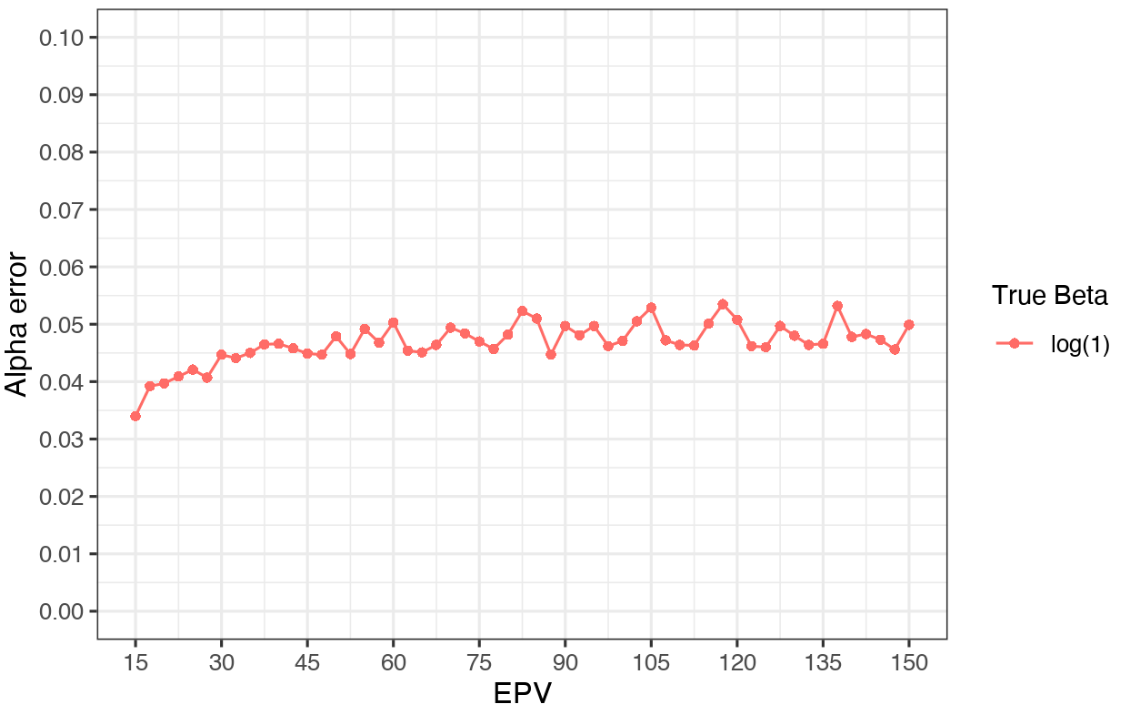
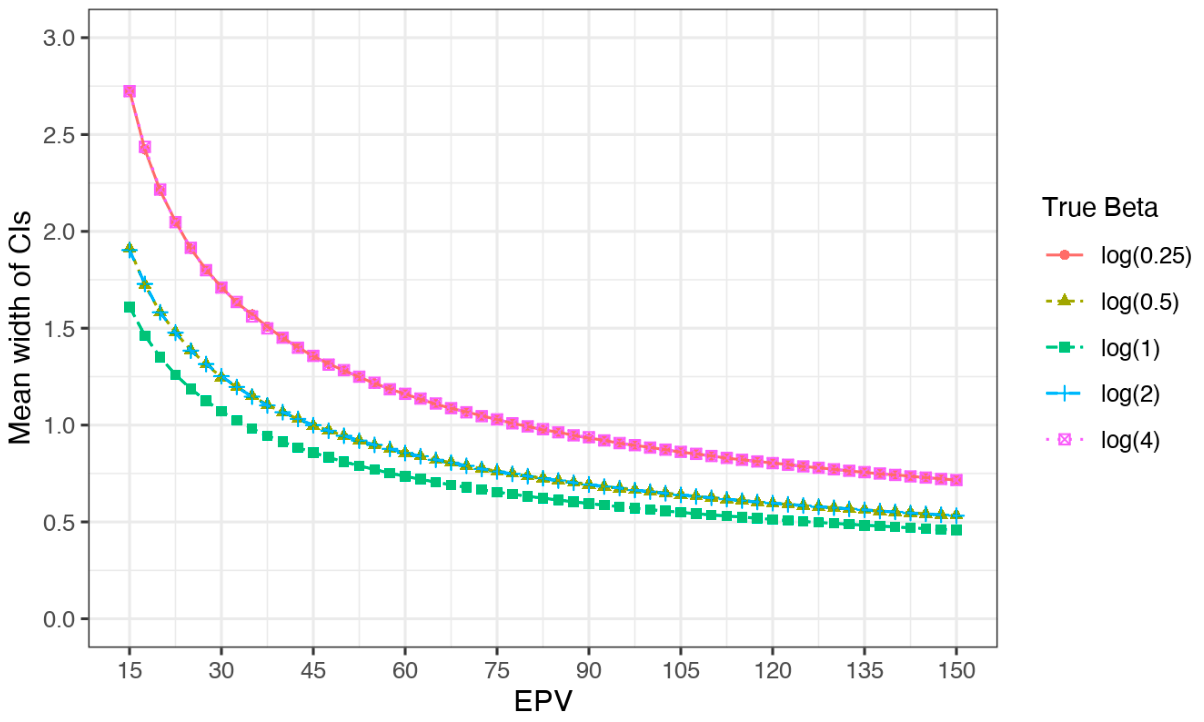
シミュレーションの結果のまとめ
- 真のオッズ比が1から離れているほど、EPVが低い時にバイアスを受けた。また、同じEPVであっても、モデルに含まれる共変量の数が少ないほどバイアスは大きくなった。EPV単体ではなくNやprevalenceも影響することが示唆された。
- EPVが15程度だと、相対バイアスが10%前後になる。共変量の数が3以上でオッズ比が2ならば8%、逆に共変量の数が2でオッズ比が4ならば12%の相対バイアスが生じた。
- さらに、同じEPVでも、アウトカムがcommonであるほどバイアスは大きくなった。アウトカム発現割合が0.1の時、相対バイアスはEPVが6であっても10%を下回った。
- EPV15よりもさらに小さい範囲を検証しているのはアウトカム発現割合を変化させたグラフだけだが、EPV15以下の範囲ではアウトカム割合に応じて相対バイアスが大きく変動していた。
- 検出力の観点では、共変量の数が2のとき、オッズが0.5や2では80%以上になるのにEPVが30以上必要であった。
本記事のまとめ
- 無事、大体の論文の再現ができた。
- 次は、正規分布に相関を持たせたり分散を大きくした事例、二項分布の事例、それらの組み合わせや、それ以外の共変量セットもうまく組み合わせられるとよい。
- また、EPVを横軸にとってPを変えるというよりは、実際にはNが決まっている中でPを増やしていく時にどのように統計的なパフォーマンスが劣化するかを見る、というのがありえるシチュエーションだと思っているので、そういう出力を出してみたい。
- forループ部分を改造して高速化もしたい(余力があれば)。
- そして、これをShinyとかのアプリにしてみたい(さらに余力があれば)。
Discussion