ベイジアンロジスティック回帰からリスク差・リスク比を出すスクラッチ実装 - メトロポリス・ヘイスティング法
ゴール
- 二値アウトカムに対してリスク比やリスク差を出す方法の一つとして、ロジスティック回帰の結果から標準化を用いるやり方を試す
- ベイジアンロジスティック回帰のMCMCに慣れる
やること
- ベイジアンロジスティック回帰メトロポリス・ヘイスティング法のスクラッチ実装する
- 特に、複数チェーンを使えることと後続の過程で
{posterior}や{bayesplot}を使えるようにする
- 特に、複数チェーンを使えることと後続の過程で
- ロジスティック回帰の結果からリスク差とリスク比を出す
対数事後分布をサンプルする関数を作成
まず、MCMC内でサンプルを生成するための関数を用意する。
特に深い意味はないが、事前分布にはstudent-t分布と多変量正規分布を用意する。モデルはロジスティック回帰なので二項分布を使う。student-tの方は各パラメータに対して同じ事前分布を独立に用意する方法にのみ対応する形となっているため、対数事前分布のstudent-tをパラメータの分だけ足し合わせる表記になっている。
# Create log posterior function ---------------------------------------
logit_st <- function(beta, prior_mean, prior_sd, degree_freedom){
# prior student-t
lnp <- LaplacesDemon::dst(beta, mu=prior_mean, sigma=prior_sd, nu=degree_freedom, log=TRUE)
# log likelihood
lnf <- dbinom(Y, size = 1, prob = LaplacesDemon::invlogit(X%*%beta), log=TRUE)
return(sum(lnp) + sum(lnf))
}
logit_mvnorm <- function(beta, prior_mean, prior_sd){
# prior multivariate normal
lnp <- LaplacesDemon::dmvn(beta, prior_mean, prior_sd, log=TRUE)
# log likelihood
lnf <- dbinom(Y, size = 1, prob = LaplacesDemon::invlogit(X%*%beta), log=TRUE)
return(lnp + sum(lnf))
}
メトロポリス・ヘイスティング法の関数を作成
次に、正規分布を提案分布とするメトロポリス・ヘイスティング法を実行する関数を作成する。
メトロポリス・ヘイスティング(MH)の実装については色々な人のコードが公開されているが、今回拘ったポイントは上で用意した2つの事前分布に1つの関数で対応できるようにしたことである。student-tを独立に充てる場合と多変量正規分布を1つ充てる場合では、パラメータの与え方が異なる。そのため、普通にMHの関数を作ろうとすると、事後分布評価の関数を変えるだけではエラーが出てしまう。
そこで、用意した事後分布評価の中身をテキストで格納し(deparse())、そこにdst()とmvnm()のいずれかが入っているかに応じて事後分布評価の関数への引数の与え方を変えるというアプローチを取った。事後分布評価の関数の種類の分だけコードが長くなってしまうのが難点だが、事前分布を変えて結果を見てみたいというときにも実行が簡単になる。
# Create MH function -----------------------------
MH <- function(X, Y, draw, burnin, num_params, step_beta, loglike,
prior_mean, prior_sd, degree_freedom=NULL) {
# count of acceptance of proposal distribution
accept_beta <- 0
# number of iterations to be saved
num_sample <- draw - burnin
result <-
array(dim=c(num_sample, num_params),
dimnames = list(num_iter = 1:num_sample,
param = paste0('beta', seq(1:num_params)-1)
)
)
# object to keep current parameter values
# initial values are stored at the beginning
temp_beta <- runif(num_params, -5, 5)
for (iter in 1:draw){
beta_o <- temp_beta # old or current parameter values
beta_n <- rnorm(num_params, temp_beta, step_beta) # proposal distribution
# get the content of function as character vectors
loglike_text <- deparse(body(loglike))
# Check if 'LaplacesDemon::dst' appears in the function body
contains_dst <- any(grepl("LaplacesDemon::dst", loglike_text))
# Check if 'LaplacesDemon::dmvn' appears in the function body
contains_dmvn <- any(grepl("LaplacesDemon::dmvn", loglike_text))
if(contains_dst) {
lnp_o <- loglike(beta_o, prior_mean, prior_sd, degree_freedom) # log posterior with old/current parameter values
lnp_n <- loglike(beta_n, prior_mean, prior_sd, degree_freedom) # log posterior with proposed parameter values
} else if (contains_dmvn) {
lnp_o <- loglike(beta_o, prior_mean, prior_sd) # log posterior with old/current parameter values
lnp_n <- loglike(beta_n, prior_mean, prior_sd) # log posterior with proposed parameter values
} else {
stop('loglike does not contain t or normal dist')
}
# accept or not
accept_true <- exp(lnp_n - lnp_o) > runif(1)
if (accept_true){
temp_beta <- beta_n # update parameter values
accept_beta <- accept_beta + 1 # count up the number of acceptance
}
if (iter>burnin){
# start storing values after burn-in
iter_num <- iter - burnin
result[iter_num,] <- temp_beta
}
Sys.sleep(1/draw)
}
return(list(result=result, acceptance=accept_beta/draw))
}
MCMC実行のコードを作成
上で作った関数を用いてMCMCを実行するパートのコードを作成する。
ここで頑張ったポイントの一つ目は各チェーンに対して別のワーカーを割り当てて並列化できるようにしたこと。並列化の関数は{doSNOW}以外にもあるのだが、ワーカーにオブジェクトをエクスポートするのを自動でやってくれるのが便利なので使っている。
ポイントの2つ目は、{posterior} and {bayesplot}を使えるようにデータの形を整えことである。これらはstanオブジェクトに対して真価を発揮するので自前実装の場合はこれらの機能の半分くらいしか使えないが、色々と便利なのでこれらのパッケージを使えるようにしたかった。
# MCMC setting
draw <- 20000
burn <- 5000
num_sample <- draw-burn
C <- 4
# step size of parameters
# to be manually adjusted to have roughly the acceptance rate of 20%
step_beta <- 0.1
# prior distributions
prior_mean <- 0 # t-dist
prior_sd <- 2.5 # t-dist
degree_freedom <- 7 # t-dist
# run MCMC using parallelizing
cl<- makeCluster(C)
registerDoSNOW(cl)
out_list <- list(NULL)
out_list <-
foreach(i=1:C) %dopar% {
MH(draw=draw,
X = X,
Y = mydata$Y,
burnin = burn,
num_params=P,
step_beta=step_beta,
loglike=logit_st,
prior_mean=prior_mean,
prior_sd=prior_sd,
degree_freedom=NULL
)
}
stopCluster(cl)
# acceptance ratio
for(i in 1:C){
print(out_list[[i]]$acceptance)
}
# Convert results list to an array
out_array <- array(dim = c(num_sample, P, C),
dimnames = list(num_iter = 1:num_sample,
param = paste0('beta', seq(1:P)-1),
chain = 1:C))
for (i in 1:C) {
out_array[,,i] <- out_list[[i]]$result
}
# Transpose the array so that posterior::as_draws_array() works
# The draws_array format assumes the dimensions in the order of (iterations, chains, variables)
out_transposed <- aperm(out_array, c(1, 3, 2))
# to use {posterior} and {bayesplot}
mcmc_draws <- posterior::as_draws_array(out_transposed)
ベイジアンロジスティック回帰の実行
1回目:1つの変数の値が大きすぎてうまく収束しないパターン
いよいよ作った関数たちの実行に移るが、今回色々試した過程を残すという意味で、うまくいかなかったケースも記録しておく。
1つ目のパターンは、用意していたトイデータの共変量の数字の大小に差があるような状況である。Modified Poissonを理解する - PART2 実装編で用いたデータでは実は変数v1を標準化していたのである。
データ作成
ということでデータ作成関数の用意。
Modified Poissonを理解する - PART2 実装編の際とは異なり、invlogit(X%*%true_beta)を使っている。
# generate a dataset -----------------------
N <- 500 # sample size
v1 <- rnorm(N, mean = 60, 10) # This guy does a bad thing
v2 <- rbinom(N, size = 1, prob = 0.5)
v3 <- rbinom(N, size = 1, prob = 0.5)
v4 <- rbinom(N, size = 1, prob = 0.5)
X <- do.call(cbind, list(1,v1,v2,v3,v4))
colnames(X) <- c('const','v1', 'v2', 'v3', 'v4')
P <- ncol(X)
true_beta <- c(-2.2, 0, 0.8, 0, 0) # true beta in the model
Y <- unlist(lapply(invlogit(X%*%true_beta), rbinom, n = 1, size = 1))
> mean(Y)
[1] 0.144
MCMCの実行
一旦はチェーン1本で実施する。
step_beta=0.1でやってみたが、以下の通り採択率が低すぎた。そこからステップサイズを下げて行きながら何度かMCMCを回しても一般的に理想的な値である20%前後には届かなかった。
> # acceptance ratio
> for(i in 1:C){
+ print(out_list[[i]]$acceptance)
+ }
[1] 0.0253
トレースプロットとACFのグラフを見てみるとうまくいっていないことが改めてよく分かる。今回のMH関数ではrnorm(num_params, temp_beta, step_beta)という風に1つの提案分布で複数のパラメータの値を探索しているので、変数v2からv4までに取っていい感じの値がサンプルされるときでもv1に対してはいい感じではない、またはその逆、といったことが起きていると思われる。
bayesplot::mcmc_trace(mcmc_draws)
bayesplot::mcmc_acf_bar(mcmc_draws)
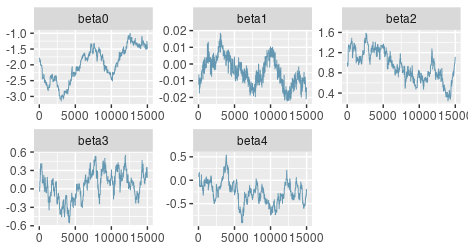
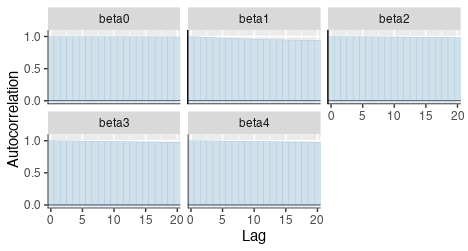
なお、MCMCpackでは高速に収束したものの、事後分布はやはりすごく裾の長い形をしていた。MCMCPackもロジスティック回帰はMHを使っているぽかったので、今後自前でMCMCをやるとなったらそういうところも理解して改善できないといけないのだろうなと思う。
2回目:大きい変数を標準化することでうまく収束したパターン
データの作成
上記データ作成工程に、下記の通り標準化プロセスを追加。
X[,2] <- scale(X[,2])
mydata <- data.frame(X[,-1],Y)
MCMCの実行
step_beta=0.1では採択率が大きかったのでstep_beta=0.2としてみたところ、採択率が20%台になった。今回はチェーンを4本にしている。
> # acceptance ratio
> for(i in 1:C){
+ print(out_list[[i]]$acceptance)
+ }
[1] 0.2225
[1] 0.21765
[1] 0.2207
[1] 0.2233
トレースプロットはいい感じになった。ACFの方を見ると自己相関が高いので、ESSは小さくなりそうではある。
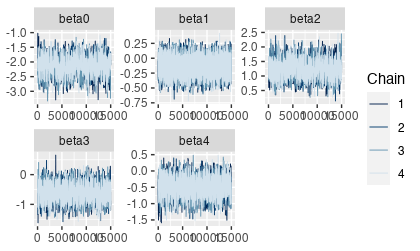
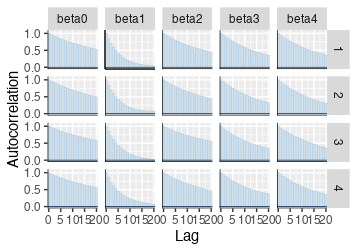
posterior::summarise_draws()で要約してみる。RhatもESSも悪くない。
> posterior::summarise_draws(mcmc_draws)
# A tibble: 5 × 10
variable mean median sd mad q5 q95 rhat ess_bulk ess_tail
<chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 beta0 -2.23 -2.22 0.262 0.254 -2.66 -1.79 1.00 981. 2018.
2 beta1 0.194 0.195 0.126 0.125 -0.0115 0.402 1.00 4434. 5994.
3 beta2 0.660 0.661 0.241 0.236 0.266 1.06 1.00 1409. 2176.
4 beta3 0.574 0.573 0.251 0.249 0.160 0.991 1.00 1361. 2669.
5 beta4 -0.150 -0.149 0.238 0.235 -0.540 0.244 1.00 1775. 3019.
検算的にglm()での結果も見てみると同等であった。
data = data.frame(X[,-1],Y)
mylogit <- glm(Y~., data, family = "binomial")
> summary(mylogit)$coefficients
Estimate Std. Error z value Pr(>|z|)
(Intercept) -2.1918748 0.2631705 -8.3287237 8.171851e-17
v1 0.1908227 0.1240920 1.5377522 1.241092e-01
v2 0.6479610 0.2475605 2.6173845 8.860648e-03
v3 0.5722244 0.2456331 2.3295899 1.982784e-02
v4 -0.1519530 0.2442932 -0.6220108 5.339347e-01
よって、MCMC実装はうまくできたと言えそう。
ロジスティック回帰からリスク比とリスク差の推定
さて、今回はロジスティック回帰からリスク比・リスク差を計算することが目的なので、収束がうまくいったN=500でv1を標準化したデータセットを再度生成し直す(seedをセットしていなかったので)。
なお、求めたいv2のリスク差とリスク比の真値は下記である。
> p1_true <- invlogit(t(c(1,0,1,0,0))%*%c(-2.2, 0, 0.8, 0, 0))
> p0_true <- invlogit(t(c(1,0,0,0,0))%*%c(-2.2, 0, 0.8, 0, 0))
# true RD
> p1_true-p0_true
[,1]
[1,] 0.09806562
# true RR
> p1_true/p0_true
[,1]
[1,] 1.983109
データの生成とMCMCの回し直しをした結果は次の通り。
> posterior::summarise_draws(mcmc_draws)
# A tibble: 5 × 10
variable mean median sd mad q5 q95 rhat ess_bulk ess_tail
<chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 beta0 -2.41 -2.40 0.298 0.294 -2.91 -1.94 1.00 984. 1438.
2 beta1 0.0835 0.0821 0.130 0.131 -0.128 0.299 1.00 4859. 6898.
3 beta2 1.03 1.02 0.278 0.277 0.581 1.49 1.00 1287. 2078.
4 beta3 -0.104 -0.103 0.257 0.259 -0.528 0.321 1.00 1463. 2486.
5 beta4 0.115 0.116 0.263 0.262 -0.315 0.552 1.01 1339. 2627.
ここからは因果推論のG-formula (regression standardization) と考え方は同じである。
一般的なやり方は、1) 手元のデータの全てのv2が1のデータセット(X_1)と0のデータセット(X_0)を作り、2) v2=1の時のリスク(p1)とv2=0の時のリスク(p0)を計算、4) リスク差やリスク比の点推定値を得るという方法である。標準誤差はデルタ法で近似して推定ができて、詳しくはFuyama et al. (2021)を参考されたい。
ベイズの場合、回帰係数のMCMCサンプルをベースにp1とp0の事後分布を得ることができる。
MHの結果から採択率の結果オブジェクトを持ってしまっているので少しデータの持ち方を調整して、
# Get RR and RD for v2 -----------------
X_0 <- X
X_0[,'v2'] <- 0
X_1 <- X
X_1[,'v2'] <- 1
res_list <- list(NULL)
for(i in 1:C) {
res_list[[i]] <- out_list[[i]]$result
}
result <-
reduce(res_list,
.f = ~ matrix(unlist(.x), ncol = P)
)
p0 <- c(invlogit(X_0%*%t(result)))
p1 <- c(invlogit(X_1%*%t(result)))
リスク差の事後分布を図示する。事後分布のサイズが大きいので1000ポイントくらいのデータを取り出している。
赤い直線が真のリスク差の値なのでいい感じに推定できていそう。
data.frame(p1,p0)[sample(1:length(p1),size=1000),] %>%
mutate(rd = p1-p0) %>%
ggplot(aes(x=rd)) +
geom_density() +
theme_classic() +
geom_vline(xintercept = p1_true-p0_true,
col = 'red')
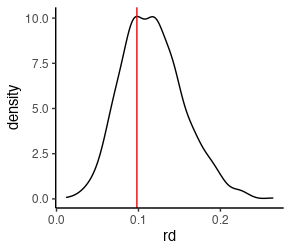
事後分布が得られていれば色々な要約統計量を出すことも簡単にできる。
> summary(p1-p0)
Min. 1st Qu. Median Mean 3rd Qu. Max.
0.001072 0.090023 0.114433 0.117137 0.141173 0.348216
> quantile(p1-p0, prob = c(0.025, 0.975))
2.5% 97.5%
0.05173695 0.19866148
> bayestestR::hdi(p1-p0)
95% HDI: [0.05, 0.19]
今度はリスク比を見てみよう。
data.frame(p1,p0)[sample(1:length(p1),size=1000),] %>%
mutate(rr = p1/p0) %>%
ggplot(aes(x=rr)) +
geom_density() +
theme_classic() +
geom_vline(xintercept = p1_true/p0_true,
col = 'red')
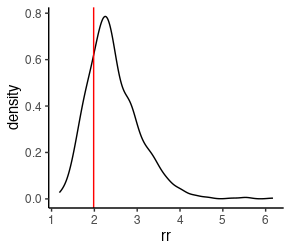
真のリスク比が2くらいだったので少し大きめに推定が出ていることになるが、悪くはないのではないだろうか。
> summary(p1/p0)
Min. 1st Qu. Median Mean 3rd Qu. Max.
1.012 2.020 2.366 2.464 2.803 6.888
> quantile(p1/p0, prob = c(0.025, 0.975))
2.5% 97.5%
1.534925 3.958758
> bayestestR::hdi(p1/p0)
95% HDI: [1.44, 3.76]
頻度論ロジスティック回帰の標準化との比較 (リスク比)
glm()を用いてロジスティック回帰を行い、上記と同じように標準化を利用してRRの点推定値と95%信頼区間を推定してみよう。
data = data.frame(X[,-1],Y)
mylogit <- glm(Y~., data, family = "binomial")
p0_f <-
predict(mylogit,
newdata = data.frame(X_0[,-1]),
type = 'response')
p1_f <-
predict(mylogit,
newdata = data.frame(X_1[,-1]),
type = 'response')
> # RD
> (rd_f <- mean(p1_f) - mean(p0_f))
[1] 0.1188854
> # RR
> (rr_f <- mean(p1_f) / mean(p0_f))
[1] 2.382858
リスク比の95% Wald信頼区間をFuyama et al. (2021)の計算式を用いて計算するとベイズの方と同じような結果を得られた。
e_0 <- exp(X_0 %*% coef(mylogit))
e_1 <- exp(X_1 %*% coef(mylogit))
R1 <- colSums(diag(as.vector(e_1/(1+e_1)^2)) %*% X_1)/sum(p1_f)
R0 <- colSums(diag(as.vector(e_0/(1+e_0)^2)) %*% X_0)/sum(p0_f)
R <- matrix(R1 - R0, nrow = 1)
var_logRR <- R%*%vcov(mylogit)%*%t(R)
> # 95% Wald CI for RR
> c(
+ exp(log(rr_f) - qnorm(0.975)*sqrt(var_logRR)),
+ exp(log(rr_f) + qnorm(0.975)*sqrt(var_logRR))
+ )
[1] 1.488992 3.813326
修正ポアソン回帰の結果との比較 (リスク比)
リスク比の推定として、修正ポアソン回帰も実行してみよう。
ロジスティック回帰と標準化で得られた結果とかなり近しい結果が得られた。
> rqlm(Y~., data=data, family=poisson, eform=T)
exp(coef) SE CL CU P-value
(Intercept) 0.0856 0.2668 0.0507 0.1443 0.0000
v1 1.0694 0.1129 0.8571 1.3342 0.5523
v2 2.3828 0.2397 1.4897 3.8114 0.0003
v3 0.9157 0.2146 0.6013 1.3947 0.6817
v4 1.0937 0.2171 0.7147 1.6736 0.6799
n=50でサンプリング運が悪かったパターンでどうなるか
データの作成
Modified Poissonを理解する - PART2 実装編で用いたn=50でかつsandwich()の実装がうまくいかなった例で試してみたパターン。このデータセットでは、
set.seed(11111111)
N <- 50 # sample size
v1 <- rnorm(N, mean = 60, 10)
v2 <- rbinom(N, size = 1, prob = 0.5)
v3 <- rbinom(N, size = 1, prob = 0.5)
v4 <- rbinom(N, size = 1, prob = 0.5)
X <- do.call(cbind, list(1,v1,v2,v3,v4))
colnames(X) <- c('const','v1', 'v2', 'v3', 'v4')
P <- ncol(X)
true_beta <- c(-2.2, 0, 0.8, 0, 0) # true beta in the model
Y <- unlist(lapply(invlogit(X%*%true_beta), rbinom, n = 1, size = 1))
X[,2] <- scale(X[,2])
mydata <- data.frame(X[,-1],Y)
> mean(Y)
[1] 0.06
> invlogit(X%*%true_beta)
[,1]
[1,] 0.19781611
[2,] 0.19781611
[3,] 0.19781611
[4,] 0.19781611
[5,] 0.19781611
[6,] 0.09975049
[7,] 0.09975049
[8,] 0.19781611
[9,] 0.09975049
[10,] 0.19781611
[11,] 0.09975049
[12,] 0.09975049
[13,] 0.09975049
[14,] 0.19781611
[15,] 0.09975049
[16,] 0.19781611
[17,] 0.19781611
[18,] 0.19781611
[19,] 0.09975049
[20,] 0.09975049
[21,] 0.19781611
[22,] 0.19781611
[23,] 0.09975049
[24,] 0.09975049
[25,] 0.09975049
[26,] 0.19781611
[27,] 0.19781611
[28,] 0.09975049
[29,] 0.19781611
[30,] 0.19781611
[31,] 0.09975049
[32,] 0.19781611
[33,] 0.09975049
[34,] 0.19781611
[35,] 0.09975049
[36,] 0.09975049
[37,] 0.09975049
[38,] 0.09975049
[39,] 0.19781611
[40,] 0.19781611
[41,] 0.09975049
[42,] 0.19781611
[43,] 0.19781611
[44,] 0.09975049
[45,] 0.09975049
[46,] 0.19781611
[47,] 0.19781611
[48,] 0.19781611
[49,] 0.19781611
[50,] 0.19781611
MCMCの実行
step_beta=1.5で採択率20%台になったが、結果を見ると
トレースとACFを見るとダメさがよく分かる。
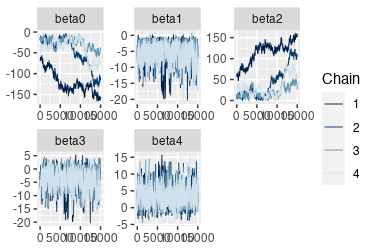
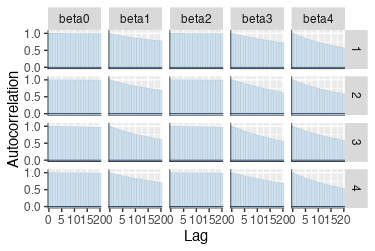
ESSも10程度しかない。推定された平均値や中央値を見ても、
> posterior::summarise_draws(mcmc_draws)
# A tibble: 5 × 10
variable mean median sd mad q5 q95 rhat ess_bulk ess_tail
<chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 beta0 -36.4 -31.8 21.5 13.8 -88.6 -13.3 1.19 18.3 11.8
2 beta1 -5.59 -5.07 2.85 2.64 -11.1 -1.87 1.00 499. 614.
3 beta2 30.0 25.3 21.3 13.4 7.56 81.5 1.20 17.8 12.1
4 beta3 -4.08 -3.76 3.12 2.98 -9.87 0.457 1.01 487. 799.
5 beta4 3.60 3.39 2.63 2.44 -0.360 8.30 1.00 681. 1045.
事前分布を変えたりMCMCの方法を変えたりすることで、このような運が悪いケースでもうまく収束することがあるのか、よく分かっていない。条件付き分布をちゃんと導出してギブスサンプリングをしたり、MHよりも効率の良いサンプリング方法にすればうまくいくのだろうか。切片項も他の回帰係数と同じ事前分布を当てているのはよくない気はする(切片の事前分布のハイパーパラメータはどう決めるのが一般的なんだろう)。
とはいえ、事前分布を置いている分、通常のglm()によるロジスティック回帰の結果よりは標準誤差が安定していた。また、ベイズの場合ESSが小さい時点で収束がうまくいっていないことが分かるのは利点だと感じた。因果推論において傾向スコアでバランスを事前に確認するように、MCMCの結果を妥当なものとして報告できるのかどうかが事前に分かるというイメージ。
> summary(mylogit)$coefficients
Estimate Std. Error z value Pr(>|z|)
(Intercept) -24.368557 4866.510267 -0.005007399 0.9960047
v1 -3.261163 2.181372 -1.495005487 0.1349130
v2 20.316053 4866.509704 0.004174666 0.9966691
v3 -2.214456 2.498229 -0.886410365 0.3753964
v4 2.308645 1.937544 1.191531596 0.2334450
しかし、修正ポアソン回帰のSEに比べるとベイズロジスティック回帰の時点で回帰係数の標準誤差が大きい。
> rqlm(Y~., data=data, family=poisson, eform=T)
exp(coef) SE CL CU P-value
(Intercept) 0.0000e+00 1.0065 0.000000e+00 0.000000e+00 0.0000
v1 2.3150e-01 0.7956 4.870000e-02 1.100800e+00 0.0659
v2 1.1549e+08 0.6056 3.524164e+07 3.784707e+08 0.0000
v3 5.7090e-01 0.7454 1.325000e-01 2.460700e+00 0.4521
v4 3.1572e+00 0.8694 5.745000e-01 1.734990e+01 0.1860
実際、リスク比を計算してみたところ下記のように発散しており、使える結果ではなかった。
> summary(p1/p0)
Min. 1st Qu. Median Mean 3rd Qu. Max.
1.000e+00 2.700e+09 1.293e+15 5.624e+46 1.386e+32 8.509e+49
感想
-
{brms}や{rstanarm}などのstanを使うパッケージでは中心化が収束効率化のためにデフォルトで行われているが、今回のような例では中心化だけでは足りず(Data Not shown)、標準化することで収束しやすくなることを体験した。収束効率を高めるための工夫の大切さを実感した。 - 事前分布の置き方を丁寧に検討したり、MCMCアルゴリズムを効率化したりできれば改善の余地はあるのだろうと思うが、二値アウトカムに対してリスク比を出したいと考えた場合には、ロジスティック回帰→標準化をよりも修正ポアソン回帰の方が万能な印象(結果も良くて実行も簡単)を持った。
- ロジスティック回帰を使う利点はリスク比とリスク差両方とも推定ができることだろうか。Nが少ないとロジスティック回帰の推定だけでなく標準化自体も精度が悪くなりそうなので、その点がネックかもしれないと思った。もっとN数が多い場合についてはFuyama et al. (2021)が性能評価しているのでそちらを参照したい。また、ロジスティック回帰の場合non-collapsibilityの問題によって上手くいかないケースもありそう。
- リスク差の標準誤差も導出して計算できたら追記したい。
Discussion