⛳
時間依存性治療のtime-to-eventデータにおける{gfoRmula}のスクラッチ実装
ゴール
- 時間依存性治療(静的レジメン)のtime-to-eventデータにおける{gfoRmula}パッケージの挙動を再現する。
- 時間依存性治療(静的レジメン)のtime-to-eventデータにおけるg-Formulaの理解を深める。
やること
- g-formulaを自作する
- {gfoRmula}を実行する
- 挙動を比較する
データ作成関数の定義
- リファクタリングの要素はたくさんある汚いコードだけれど、これでとりあえず動く。
- 治療Aはバイナリ変数。
gen_longitudinal_survival_data <-
function(N = 1000,
T_max = 3,
p = 2,
beta1 = c(0.5, -0.3), # 交絡因子X_tのアウトカムに対する影響
beta2 = c(0.1, -0.1), # 交絡因子X_{t-1}のアウトカムに対する影響
gamma1 = 1.0, # 治療A_tのアウトカムY_tに対する影響
gamma2 = 0.5, # 治療A_{t-1}のアウトカムY_tに対する影響
alpha = c(-0.5, 0.5), # 交絡因子の治療に対する影響
delta = 0.2, # 治療の交絡因子に対する影響
rho = 0.1, # A_{t-1}のA_tへの影響
lambda = 0.1 # アウトカムのベースラインハザード
) {
data_list <- list()
rows_time0_list <- list()
true_outcomes <-
expand.grid(id = 1:N, time = 0:(T_max)) %>%
arrange(id, time) %>%
mutate(Y_prob_0 = NA, Y_prob_1 = NA)
for (i in 1:N) {
# default: no event occurs, so set T_obs to the maximum possible
T_obs <- T_max + 1
X_mat <- matrix(0, nrow = T_max+1, ncol = p)
X_mat_ext <- matrix(0, nrow = T_max+1, ncol = p+1)
A_vec <- integer(T_max+1) # 治療ベクトルの初期化:要素が0で長さがT_max+1のベクトル
# 初期共変量(ベースライン)
X_mat[1, ] <- rnorm(p, 0.1)
X_mat_ext[1, ] <- c(X_mat[1, ], 0) # 治療A_{t-1}=0
# 共変量・治療の時系列更新
# X_{t-1}とA_{t-1}の関数からX_{t}を生成(confounder-treatment feedbackあり)
# t = 1はベースラインとして上で作ったのでt = 2からデータを作る
for (t in 2:(T_max+1)) {
X_mat[t, ] <- X_mat[t - 1, ] + delta * A_vec[t - 1] + rnorm(p, 0, 0.1)
X_mat_ext[t, ] <- matrix(c(X_mat[t, ], A_vec[t - 1]), nrow = 1)
# A_tはXとA_{t-1}の関数から生成
alpha_ext <- c(alpha, rho)
linpred <- X_mat_ext[t, ] %*% alpha_ext
p_treat <- plogis(linpred)
A_vec[t] <- rbinom(1, 1, p_treat)
}
# 観測された治療に基づく生存時間(指数分布)
# アウトカムはXとAの関数から生成
status <- integer(T_max+1) # アウトカムの初期化
A_prev <- c(0, A_vec[1:T_max])
# piecewise‐constant hazards model
for (t in 2:(T_max+1)) {
hazard <- lambda * exp(beta1 %*% X_mat[t, ] + beta2 %*% X_mat[t - 1, ] + gamma1 * A_vec[t] + gamma2 * A_prev[t])
p_event <- 1 - exp(-hazard) # exponential dist
status[t]<- rbinom(1, 1, p_event)
if (status[t]==1) {
T_obs <- t # event in interval t
break
}
}
# long format(各ビジットで生存 or イベント確認)
t_now <-1
alive <- TRUE
# t_nowは時点を入力するもので
# tのループは行数を参照するためのインデックス
for (t in 2:(T_max + 1)) {
if (!alive) break
t_next <- t_now + 1
endtime <- min(T_obs, t_next)
data_list[[length(data_list) + 1]] <-
data.frame(
id = i,
starttime = t_now,
endtime = ceiling(endtime),
time = t_now,
X1 = X_mat[t, 1],
X2 = X_mat[t, 2],
A = A_vec[t],
status = status[t]
)
if (status[t] == 1) alive <- FALSE
t_now <- t_next
}
rows_time0_list[[i]] <-
data.frame(id = i, starttime = 0, endtime = 1, time = 0,
X1 = X_mat[1, 1], X2 = X_mat[1, 2], A = 0, status = 0)
}
long_data <- bind_rows(data_list)
long_data_out <-
long_data %>%
bind_rows(rows_time0_list) %>%
arrange(id, time)
return(list(data = long_data_out))
}
データの生成
- 3時点のデータを作成する。
T_max <- 3
sim <-
gen_longitudinal_survival_data(
N = 1000,
T_max = 3,
p = 2,
beta1 = c(0.5, -0.3), # 交絡因子X_tのアウトカムに対する影響
beta2 = c(0.1, -0.1), # 交絡因子X_{t-1}のアウトカムに対する影響
gamma1 = 1.0, # 治療A_tのアウトカムY_tに対する影響
gamma2 = 0.5, # 治療A_{t-1}のアウトカムY_tに対する影響
alpha = c(-0.5, 0.5), # 交絡因子の治療に対する影響
delta = 0.2, # 治療の交絡因子に対する影響
rho = 0.1, # A_{t-1}のA_tへの影響
lambda = 0.1 # アウトカムのベースラインハザード
)
> head(sim$data)
id starttime endtime time X1 X2 A status
1 1 0 1 0 0.7207567 0.1356414 0 0
2 1 1 2 1 0.7980722 0.2628903 1 0
3 1 2 3 2 1.0155902 0.6296745 0 0
4 1 3 4 3 1.0075913 0.5951780 1 1
5 2 0 1 0 -1.6550540 -0.3209638 0 0
6 2 1 2 1 -1.5785631 -0.2143476 1 1
潜在アウトカムの理論値の確認
- 3時点のAlways treatとNever treatの静的レジメンにおける累積発現割合の理論値を得る。
sigmat <- matrix(c(0.1, 0, 0, 0.1), ncol = 2, byrow = TRUE)
lambda <- 0.1
gamma <- c(1, 0.5) # 治療A_tとA_{t-1}のアウトカムに対する影響
a1_t1 <- c(1, 0) # t=1, t=0
a1_t2 <- c(1, 1) # t, t-1
a0 <- c(0, 0)
delta <- 0.2 # 治療の交絡因子に対する影響
beta1 = c(0.5, -0.3) # 交絡因子X_tのアウトカムに対する影響
beta2 = c(0.1, -0.1) # 交絡因子X_{t-1}のアウトカムに対する影響
p_mat <- matrix(NA, ncol = 2, nrow = 3)
x_list <- list()
p1_list <- list()
p0_list <- list()
n <- 10000
for(t in 1:3) {
if(t > 1) {
a1 <- a1_t2
} else {
a1 <- a1_t1
}
if (t == 1) {
x <- MASS::mvrnorm(n = n, mu = c(0, 0), Sigma = sigmat)
x_list[[t]] <- x
} else {
x_mean <- x_list[[t - 1]] + sum(delta * a1)
x_tmp <- matrix(NA, ncol = 2, nrow = n)
for(i in 1:n) {
x_tmp[i,] <- MASS::mvrnorm(n = 1, mu = c(x_mean[i, 1], x_mean[i, 2]), Sigma = sigmat)
}
x_list[[t]] <- x_tmp
}
if (t > 1){
x_lag <- x_list[[t-1]]
} else {
x_lag <- matrix(0, ncol = 2, nrow = n)
}
x_mat <- cbind(x, x_lag)
h1 <- lambda * exp(x_mat %*% c(beta1, beta2) + sum(a1 * gamma))
p1 <- 1 - exp(-h1)
p1_list[[t]] <- p1
h0 <- lambda * exp(x_mat %*% c(beta1, beta2) + sum(a0 * gamma))
p0 <- 1 - exp(-h0)
p0_list[[t]] <- p0
p1_mean <- mean(p1)
p0_mean <- mean(p0)
p_mat[t, 1] <- p1_mean
p_mat[t, 2] <- p0_mean
cat("time t = ", t, "p1 = ", p1_mean, "p0 = ", p0_mean, "\n")
}
time t = 1 p1 = 0.2401443 p0 = 0.09637084
time t = 2 p1 = 0.3644626 p0 = 0.09706298
time t = 3 p1 = 0.3645725 p0 = 0.09712847
- それぞれの時点のデータを縦に積む。
sim_raws <-
data.frame(
id = rep(1:n, 3),
time = rep(c(1, 2, 3), each = n),
p1 = do.call(rbind, p1_list),
p0 = do.call(rbind, p0_list),
do.call(rbind, x_list)
)
> head(sim_raws)
id time p1 p0 X1 X2
1 1 1 0.1973766 0.07770072 -0.23562399 0.31441153
2 2 1 0.2474333 0.09929319 0.04690121 -0.07096115
3 3 1 0.2245835 0.08932754 -0.30483119 -0.28658805
4 4 1 0.2056820 0.08122324 0.09749714 0.71553443
5 5 1 0.2167095 0.08593644 -0.06913840 0.24133935
6 6 1 0.2225286 0.08844046 0.02112285 0.29153387
# true potential outcomes - cumulative event probability
sim_raws %>%
group_by(id) %>%
mutate(
risk1 = 1 - cumprod(1-p1),
risk0 = 1 - cumprod(1-p0)
) %>%
ungroup() %>%
summarise(ypo1 = mean(risk1),
ypo0 = mean(risk0),
rd = ypo1 - ypo0,
rr = if_else(is.na(ypo1/ypo0), 0 , ypo1/ypo0),
.by = time)
# A tibble: 3 × 5
time ypo1 ypo0 rd rr
<dbl> <dbl> <dbl> <dbl> <dbl>
1 1 0.240 0.0964 0.144 2.49
2 2 0.515 0.184 0.331 2.80
3 3 0.687 0.262 0.424 2.62
データ整形
df_long <- sim$data
df_long_l1 <-
df_long %>%
arrange(id, time) %>%
group_by(id) %>%
mutate(across(everything(), ~ lag(., n = 1))) %>%
mutate(time = time + 1) %>%
ungroup() %>%
filter(!is.na(time)) %>%
dplyr::select(id, time, X1_l1 = X1, X2_l1 = X2, A_l1 = A)
df_gformula <-
df_long %>%
left_join(df_long_l1, by = c("id", "time")) %>%
# gformulaには不要
dplyr::select(-starttime, -endtime)
# あとで{gfoRmula}を使う際のデータセット作成に使う
df_gformula_copy <- df_gformula
df_gformula <-
df_gformula %>%
# X_1やA_1を作るためにtime=0のベースライン共変量が必要だっただけなので除く
filter(time > 0)
生成されたデータの確認
-
X1とX2は対して動いておらず、Aが一番動いているデータになっていた。
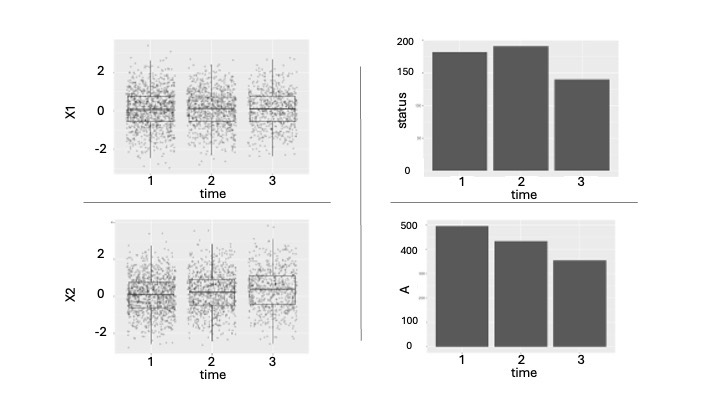
-
baselineでの治療Aの状態で層別したKM曲線。理論値とは異なることがわかる。
# ベースラインの治療で層別した場合のKM
df_gformula_surv <-
df_gformula %>%
left_join(
df_gformula %>%
filter(time == 1) %>%
select(id, A_base = A) ,
by = c("id")
)
df_gformula_surv %>%
distinct(id, A_base) %>%
summarise(A_n = sum(A_base))
survfitobj2 <- survfit(Surv(event = status, time = time) ~ factor(A_base),
data = df_gformula_surv)
summary(survfitobj2, times = c(1, 2, 3))
survminer::ggsurvplot(
survfitobj2,
data = df_gformula_surv,
conf.int = TRUE,
fun = "event"
)

g-formulaの自作
モデルフィッティング
- pooledデータにモデルフィッティングする。
- ここでのポイントは{gfoRmula}ではlag(1)を用いる場合、t>1以降のデータを使ったcovariate modelsを作ることである。prebaselineの情報(t<0の行)が存在していてもそういう仕様になっているぽいのでそれに合わせた。
- 実データ解析ではtimeを柔軟にモデリングしたり、交互作用を入れたりするが、今回は元々のデータがそのような複雑性を持っていないので割愛した。
# 共変量のモデル
## NB: gformulaパッケージの方では、共変量モデルにおいてはi時点前までのラグ変数を作成する場合、
## 共変量モデルをフィットするデータセットから、time = t <= 最大ラグi_max のレコードを除外する
## 今回のケースではi_max = 1なので、 t > 1のみのデータを用いてフィッティングする
model_X1 <- glm(X1 ~ A_l1 + X1_l1 + X2_l1,
data = subset(df_gformula, time > 1), family = gaussian())
model_X2 <- glm(X2 ~ A_l1 + X1_l1 + X2_l1
data = subset(df_gformula, time > 1), family = gaussian())
# アウトカムモデル
model_Y <-
glm(
status ~ A + A_l1 + X1 + X2 + X1_l1 + X2_l1,
data = df_gformula, family = binomial()
)
predict関数
- 次に、フィットしたモデルから予測するための関数を定義する。ここでノイズを足す関数と、ノイズを足さない関数を定義した。最終的にはどちらにしても結果は変わらなかった。
# 不確実性を考慮しない場合のpredict関数
pred_deterministic <- function(model, newdata) {
preds <- predict(model, newdata=newdata, type="response")
return(preds)
}
# 線形モデルからのpredict with model fitting uncertainty
predict_normal_with_noise <- function(model, newdata) {
# モデルマトリクスの構築(interceptや係数対応のため)
X_design <- model.matrix(delete.response(terms(model)), newdata)
# 係数の再サンプリング(多変量正規分布から1つサンプル)
beta_hat <- coef(model)
V_hat <- vcov(model)
beta_sample <- MASS::mvrnorm(n = 1, mu = beta_hat, Sigma = V_hat)
# 線形予測値(固定効果)
pred_mean <- X_design %*% beta_sample
# 誤差項(ランダムノイズ)
eps <- rnorm(n = nrow(newdata), mean = 0, sd = sigma(model))
# 総和
pred_sim <- as.numeric(pred_mean + eps)
return(pred_sim)
}
# glmからのpredict with model fitting uncertainty
predict_glm_with_noise <-
function(model, newdata) {
beta_hat <- coef(model)
Sigma_hat <- vcov(model)
# design matrix for newdata (including intercept)
Xnew <- model.matrix(delete.response(terms(model)), newdata)
# sample B coefficient vectors
beta_boot <- MASS::mvrnorm(n = 1, mu = beta_hat, Sigma = Sigma_hat)
# compute B sets of probabilities
# result: matrix of dim (nrow(newdata) × B)
lp_mat <- Xnew %*% (beta_boot)
p_mat <- plogis(lp_mat)
return(p_mat)
}
モンテカルロシミュレーション用の関数定義
- 今回求めたいのは静的レジメンなので、Aは関数の引数として指定するのみ。
# G-formulaのMCの1イテレーションを実行する関数
mcmc_one_iter <- function(.df_gformula, a_hypo) {
# a_hypoにはhypotheticalなA=aの値を入れる
N <- length(unique(.df_gformula$id))
# G-formulaなので仮想的なA=aを指定する
df_sim_out <-
expand.grid(id = c(1:N), time = c(1:(T_max)),
A_l1 = NA) %>%
mutate(
A = a_hypo, # static policy from t=1 onward
status = 0,
at_risk = 1,
hazard = NA
) %>%
# time = 1 でのX値を結合する
left_join(
.df_gformula %>%
filter(time == 1) %>%
dplyr::select(id, time, X1, X2, X1_l1, X2_l1),
by = c("id", "time")
) %>%
arrange(id, time)
# G-formulaなので仮想的なA_l1も値を指定する
df_sim_out$A_l1[df_sim_out$time <= 1] <- 0 # t=1が初回投与なのでA_lag1=0
df_sim_out$A_l1[df_sim_out$time > 1] <- a_hypo
for (t in 1:(T_max)) {
# now simulate X_t using the correct A_l1, X_l1 …
idxX_current <- which(df_sim_out$time == t)
idxX_next <- which(df_sim_out$time == t+1)
# add the predicted X values to the lag value columns of rows at next time t+1
df_sim_out$X1_l1[idxX_next] <- df_sim_out$X1[idxX_current]
df_sim_out$X2_l1[idxX_next] <- df_sim_out$X2[idxX_current]
df_sim_out$X1[idxX_next] <- predict_normal_with_noise(model = model_X1, newdata = df_sim_out[idxX_next, ])
df_sim_out$X2[idxX_next] <- predict_normal_with_noise(model = model_X2, newdata = df_sim_out[idxX_next, ])
# simulate p_{t+1} for all including those not at risk anymore.
idx_pt <- which(df_sim_out$time == t)
# simulate Y_{t+1} only for those still at risk
idxY <- which(df_sim_out$time == t & df_sim_out$at_risk == 1)
if (length(idx_pt) > 0) {
# p_t <- predict(model_Y, newdata = df_sim_out[idx_pt, ], type = "response")
p_t <- predict_glm_with_noise(model = model_Y, newdata = df_sim_out[idx_pt, ])
df_sim_out$hazard[idx_pt] <- p_t
rel_idxY <- df_sim_out$at_risk[idx_pt] == 1
y_t <- rbinom(sum(rel_idxY), 1, p_t[rel_idxY])
df_sim_out$status[idxY] <- y_t
ids_event <- df_sim_out$id[idxY][y_t == 1]
df_sim_out$at_risk[
df_sim_out$id %in% ids_event &
df_sim_out$time > t
] <- 0
}
}
df_sim_out$hazard[is.na(df_sim_out$hazard)] <- 0
return(df_sim_out)
}
g-formulaの実行
N_sim <- 1000
tic()
df_sim_gformula <-
lapply(1:N_sim, function(simID) {
df_sim_untreat <- mcmc_one_iter(df_gformula, a_hypo = 0)
df_sim_treat <- mcmc_one_iter(df_gformula, a_hypo = 1)
rbind(
data.frame(hypo_interv = "Never treated", df_sim_untreat),
data.frame(hypo_interv = "Always treated", df_sim_treat)
) %>%
mutate(sim_n = simID)
}) %>%
bind_rows() %>%
mutate(hypo_interv = factor(hypo_interv, levels = c("Never treated", "Always treated")))
toc()
23.058 sec elapsed
結果の確認
- 全体的に少し高めに推定しているもののいい感じの結果となっていると思う。
get_df_surv <-
function(.data) {
out <-
.data %>%
arrange(sim_n, hypo_interv, id, time) %>%
group_by(sim_n, hypo_interv, id) %>%
mutate(risk = 1 - cumprod(1 - hazard)) %>%
ungroup() %>%
dplyr::select(hypo_interv, id, time, risk)
return(out)
}
get_df_risk_mean <-
function(.data) {
out <-
.data %>%
group_by(hypo_interv, time) %>%
summarise(
R_mean = mean(risk),
.groups = "drop"
)
return(out)
}
df_surv <- get_df_surv(df_sim_gformula)
df_risk_mean <-
get_df_risk_mean(df_surv)
df_risk_wide <-
df_risk_mean %>%
tidyr::pivot_wider(names_from = hypo_interv,
values_from = c(R_mean))
df_effect <-
df_risk_wide %>%
mutate(
RD = `Always treated` - `Never treated`,
RR = `Always treated` / `Never treated`,
) %>%
mutate(RR = if_else(is.na(RR), 1, RR))
> df_effect
# A tibble: 3 × 5
time `Never treated` `Always treated` RD RR
<dbl> <dbl> <dbl> <dbl> <dbl>
1 1 0.117 0.270 0.153 2.31
2 2 0.213 0.558 0.345 2.62
3 3 0.294 0.716 0.422 2.44
ブートストラップ
ブートストラップの中で使う1反復分の関数定義
- ある個人から複数時点の行が存在するので、その点を考慮したブロックブートストラップサンプリングになるようにする必要がある。
- ブートストラップCIを構成する際は、各ブートストラップ内で平均値を取ってその分布から作るのではなく、ブートストラップサンプル全体の分布からquantile-baseで構成している。このやり方が本当に正しいのかについては詳しい説明を見つけられていないが、後ほど試す{gfoRmula}のブートストラップと近しい値になるので一旦この方法としている。
- また、ブートストラップを行うと計算時間が膨大になるため、1回のMCシミュレーションの反復回数をオリジナルサンプルサイズよりも小さくしてブートストラップ回数を増やすという方法がありえるような気もしているが、この辺りもあまり調べられていない。
mcmc_one_iter_boot <- function(.df_gformula, a_hypo,
.model_X1, .model_X2, .model_Y) {
# a_hypoにはhypotheticalなA=aの値を入れる
N <- length(unique(.df_gformula$id))
# G-formulaなので仮想的なA=aを指定する
df_sim_out <-
expand.grid(id = c(1:N), time = c(1:(T_max)),
A_l1 = NA) %>%
mutate(
A = a_hypo, # static policy from t=1 onward
status = 0,
at_risk = 1,
hazard = NA
) %>%
# time = 1 でのX値を結合する
left_join(
.df_gformula %>%
filter(time == 1) %>%
dplyr::select(id, time, X1, X2, X1_l1, X2_l1),
by = c("id", "time")
) %>%
arrange(id, time)
# G-formulaなので仮想的なA_l1も値を指定する
df_sim_out$A_l1[df_sim_out$time <= 1] <- 0 # t=1が初回投与なのでA_lag1=0
df_sim_out$A_l1[df_sim_out$time > 1] <- a_hypo
for (t in 1:(T_max)) {
# now simulate X_t using the correct A_l1, X_l1 …
idxX_current <- which(df_sim_out$time == t)
idxX_next <- which(df_sim_out$time == t+1)
# add the predicted X values to the lag value columns of rows at next time t+1
df_sim_out$X1_l1[idxX_next] <- df_sim_out$X1[idxX_current]
df_sim_out$X2_l1[idxX_next] <- df_sim_out$X2[idxX_current]
df_sim_out$X1[idxX_next] <- predict_normal_with_noise(model = model_X1, newdata = df_sim_out[idxX_next, ])
df_sim_out$X2[idxX_next] <- predict_normal_with_noise(model = model_X2, newdata = df_sim_out[idxX_next, ])
# simulate p_{t+1} for all including those not at risk anymore.
idx_pt <- which(df_sim_out$time == t)
# simulate Y_{t+1} only for those still at risk
idxY <- which(df_sim_out$time == t & df_sim_out$at_risk == 1)
if (length(idx_pt) > 0) {
#p_t <- predict(model_Y, newdata = df_sim_out[idx_pt, ], type = "response")
p_t <- predict_glm_with_noise(model = model_Y, newdata = df_sim_out[idx_pt, ])
df_sim_out$hazard[idx_pt] <- p_t
rel_idxY <- df_sim_out$at_risk[idx_pt] == 1
y_t <- rbinom(sum(rel_idxY), 1, p_t[rel_idxY])
df_sim_out$status[idxY] <- y_t
ids_event <- df_sim_out$id[idxY][y_t == 1]
df_sim_out$at_risk[
df_sim_out$id %in% ids_event &
df_sim_out$time > t
] <- 0
}
}
return(df_sim_out)
}
ブートストラップの1反復分の定義
gformula_boot <-
function(.original_data, b, .N_sim) {
# 1) bootstrap-sample the original data
ids <- unique(.original_data$id)
ids_boot <- sample(ids, size = length(ids), replace = TRUE)
# 同じidでも繰り返し取ってスタックする
# かつ取ってきたオリジナルidを新しいidに書き換える
df_boot <- map2_dfr(
.x = ids_boot,
.y = ids, # idsがどうせ1:Nの整数配列なので、これを与えれば新しいid列になる
~ .original_data %>%
filter(id == .x) %>%
#mutate(original_id = id) %>% # 下流のデータには残らないけどオリジナルidの保存
mutate(id = .y) # mcmc_one_iter()内でid列を使うので新しい列名にしないこと
)
# 共変量のモデル
model_X1_boot <- glm(X1 ~ A_l1 + X1_l1 + X2_l1, data = subset(df_boot, time > 1), family = gaussian())
model_X2_boot <- glm(X2 ~ A_l1 + X1_l1 + X2_l1 , data = subset(df_boot, time > 1), family = gaussian())
# アウトカムモデル
model_Y_boot <-
glm(
status ~ A + A_l1 + X1 + X2 + X1_l1 + X2_l1,
data = df_boot, family = binomial()
)
res_inner <- map_dfr(
1:.N_sim,
function(simID) {
df0 <- mcmc_one_iter_boot(df_boot, a_hypo = 0,
.model_X1 = model_X1_boot, .model_X2 = model_X2_boot, .model_Y = model_Y_boot)
df1 <- mcmc_one_iter_boot(df_boot, a_hypo = 1,
.model_X1 = model_X1_boot, .model_X2 = model_X2_boot, .model_Y = model_Y_boot)
bind_rows(
tibble(hypo_interv = "Never treated", df0),
tibble(hypo_interv = "Always treated", df1)
) %>%
mutate(sim_n = simID)
}
) %>%
mutate(
hypo_interv = factor(hypo_interv,
levels = c("Never treated","Always treated")),
boot_n = b
)
# to avoid loading all the massive bootstrap data
# get aggregated results here
# return
return(res_inner)
}
ブートストラップの実行
- 10回リサンプリングするブートストラップ。
- {future}に関連する用量制限に引っかかったので用量制限を引き上げるオプションを追加した。
library(future)
library(furrr)
library(parallel)
N_boot = 10
N_sim = 1000
# By default, future refuses to export objects > 500 MB.
# allow up to 5 GB of globals
options(future.globals.maxSize = 5 * 1024^3)
# 1) Create PSOCK cluster
workers <- parallel::detectCores() - 1
cl <- makeCluster(workers)
plan(cluster, workers = cl)
# 2) Export data, models, and all custom functions
clusterExport(cl, varlist = c(
"df_gformula",
"mcmc_one_iter_boot",
"gformula_boot", "N_boot", "N_sim"
))
# 3) Load required packages on each worker
clusterEvalQ(cl, {
library(dplyr)
library(purrr)
library(MASS)
RNGkind("L'Ecuyer-CMRG")
})
tic()
# 4) Now run your future_map without re‐shipping df_gformula
df_bootstrap_results <- future_map_dfr(
1:N_boot,
~gformula_boot(b=., .N_sim = N_sim, .original_data = df_gformula),
.options = furrr_options(seed = TRUE),
.progress = TRUE
)
df_risk_summary <-
df_bootstrap_results %>%
# Calculate risk for each individual simulation
group_by(boot_n, sim_n, hypo_interv, id) %>%
arrange(time) %>%
mutate(risk = 1 - cumprod(1 - hazard)) %>%
ungroup() %>%
# Average within each bootstrap×simulation combination
group_by(boot_n, sim_n, hypo_interv, time) %>%
summarise(R = mean(risk), .groups = "drop") %>%
# Now calculate CIs across all bootstrap×simulation combinations
group_by(hypo_interv, time) %>%
summarise(
R_mean = mean(R),
R_lwr = quantile(R, prob = 0.025),
R_upr = quantile(R, prob = 0.975),
.groups = "drop"
)
# 5) When you’re done
plan(sequential)
stopCluster(cl)
toc()
168.792 sec elapsed
ブートストラップの結果確認
df_risk_summary
# A tibble: 6 × 5
hypo_interv time R_mean R_lwr R_upr
<fct> <dbl> <dbl> <dbl> <dbl>
1 Never treated 1 0.116 0.0997 0.135
2 Never treated 2 0.213 0.191 0.235
3 Never treated 3 0.293 0.270 0.317
4 Always treated 1 0.268 0.240 0.299
5 Always treated 2 0.557 0.520 0.593
6 Always treated 3 0.716 0.687 0.743
- 各種プロットでも視覚的に確認する。
# cumulative prob plot
plot_prob <-
function(.data, CI = TRUE) {
p <- ggplot(.data, aes(x = time, y = R_mean, color = hypo_interv)) +
geom_line(linewidth = 1.2) +
geom_point(size = 2) +
labs(
title = "Cumulative Incidence Curve (G-formula)",
y = "Cumulative Event Probability", x = "Time"
) +
theme_minimal()
# Conditionally add the ribbon
if (CI) {
p <- p + geom_ribbon(aes(ymin = R_lwr, ymax = R_upr,
fill = hypo_interv), alpha = 0.3)
}
return(p)
}
# RD plot
plot_RD <-
function(.data, CI = TRUE) {
p <- ggplot(.data, aes(x = time, y = RD)) +
geom_line(linewidth = 1.2, color = "darkblue") +
geom_point(size = 2, color = "darkblue") +
geom_hline(yintercept = 0, linetype = "dashed") +
labs(
title = "Risk Difference Over Time (Always - Never treated)",
x = "Time",
y = "Risk Difference"
) +
theme_minimal()
# Conditionally add the ribbon
if (CI) {
p <- p + geom_ribbon(aes(ymin = RD_lwr, ymax = RD_upr), alpha = 0.2)
}
return(p)
}
# RR plot
plot_RR <-
function(.data, CI = TRUE) {
p <- ggplot(.data, aes(x = time, y = RR)) +
geom_line(linewidth = 1.2, color = "darkblue") +
geom_point(size = 2, color = "darkblue") +
geom_hline(yintercept = 1, linetype = "dashed") +
labs(
title = "Risk Ratio Over Time (Always / Never treated)",
x = "Time",
y = "Risk Ratio"
) +
theme_minimal()
# Conditionally add the ribbon
if (CI) {
p <- p + geom_ribbon(aes(ymin = RR_lwr, ymax = RR_upr), alpha = 0.3)
}
return(p)
}
# 累積発現確率プロット
plot_prob(df_risk_summary, CI = TRUE)
# RD プロット
plot_RD(df_effect, CI = TRUE)
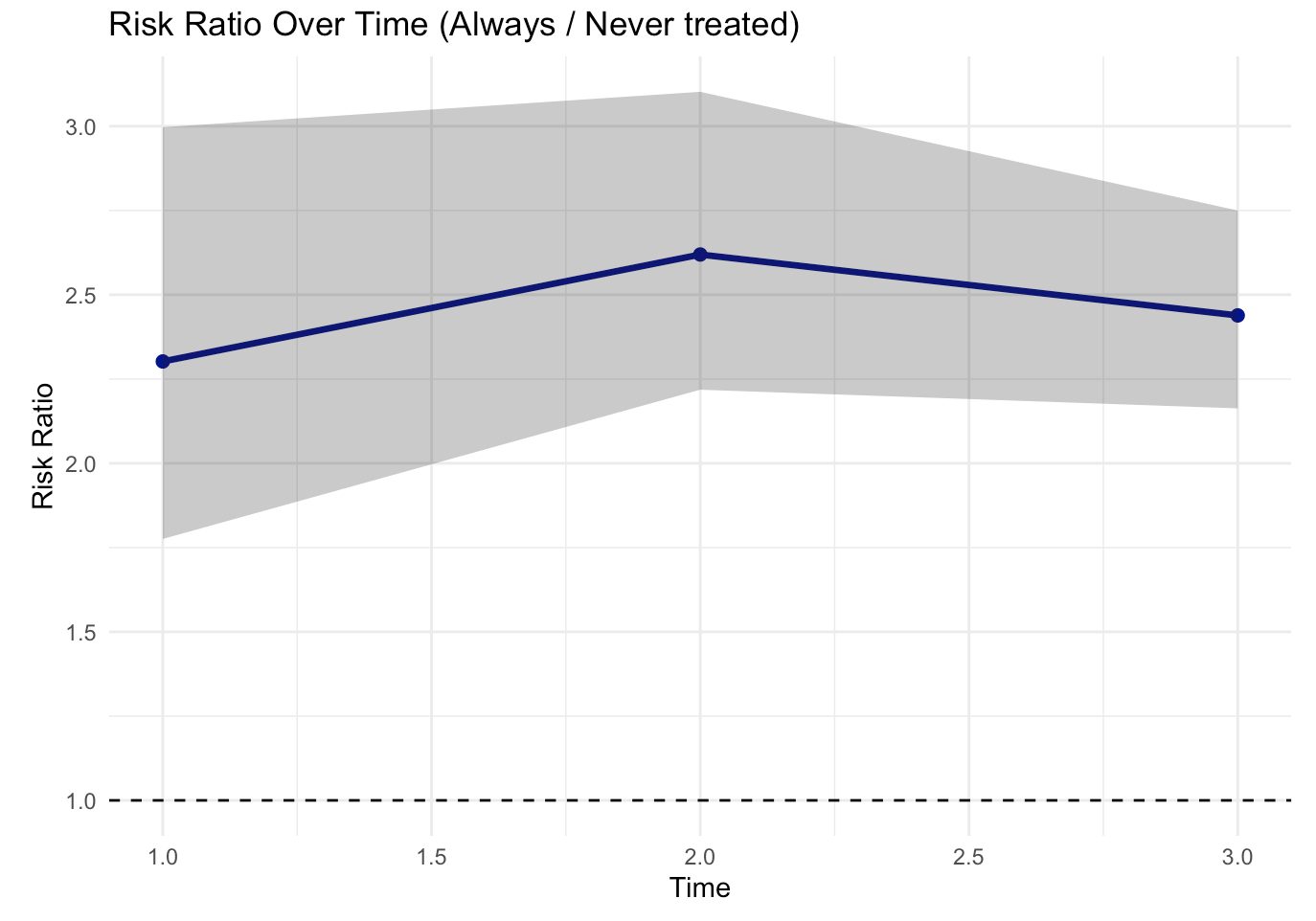
# RRのプロット
plot_RR(df_effect)


{gfoRmula}
下準備
- {gfoRmula}は開始時点を0にし{data.table}オブジェクトにする必要がある。
library(gfoRmula)
library(data.table)
dt_gformula <-
df_gformula_copy %>%
arrange(id, time) %>%
mutate(time = time - 1) %>%
as.data.table()
関数の実行
- 自作と比べると高速すぎる(data.tableはやはり速いのだろう)。
- 静的な決定的治療レジームだったらAの式はいらない気がするのだけど、指定しないとエラーになって実行できない。これはnatural courseの推定に必要になっている。
-
baselagsという引数は、pre-baseline times (t < 0)のレコードがデータに入っていない場合に、lagなどの共変量の処理がどう行われるかを調整する。 -
baselags = TRUEにした場合、t = 0の時の共変量の値がcarry backwardされる。一方、baselags = FALSEにした場合には、連続量ならば0、カテゴリ変数ならば参照水準で補完される。
covparams <- list(
covmodels = c(
X1 ~ lag1_A + lag1_X1 + lag1_X2,
X2 ~ lag1_A + lag1_X1 + lag1_X2,
A ~ lag1_A + lag1_X1 + lag1_X2
)
)
ymodel <- status ~ A + lag1_A + X1 + X2 + lag1_X1 + lag1_X2
tic()
gformula_fit <-
gformula(
outcome_type = 'survival',
obs_data = dt_gformula,
id = 'id',
time_name = 'time',
outcome_name = 'status',
covnames = c('X1', 'X2', 'A'),
histories = c(lagged),
histvars = list(c('X1', 'X2', 'A')),
covtypes = c('normal', 'normal', 'binary'),
covparams = covparams,
ymodel = ymodel,
time_points = 3,
intvars = list('A', 'A'),
int_descript = c('Never treat', 'Always treat'),
interventions = list(
list(c(static, rep(0, 3))),
list(c(static, rep(1, 3)))
),
nsimul = 1000,
baselags = TRUE, #pre-baseline情報がある場合にはT/Fどちらでも変わらない
model_fits = TRUE,
sim_data_b = TRUE,
seed = 1234)
toc()
0.184 sec elapsed
結果の確認
- 時点ごとの結果を確認したいので
resultを見る - 自作関数と近い値が得られた。
- 0がNatural course, 1がNever treated、2がAlways treatedになっている
- リスク比とリスク差はnatural courseとの比較になっているので、先に計算したものとの比較対象とはなっていない。
> gformula_fit$result
Index: <k>
k Interv. NP Risk g-form risk Risk ratio Risk difference % Intervened On
<num> <num> <num> <num> <num> <num> <num>
1: 0 0 0.182 0.1796748 1.0000000 0.00000000 NA
2: 0 1 NA 0.1160781 0.6460458 -0.06359665 NA
3: 0 2 NA 0.2682741 1.4931094 0.08859932 NA
4: 1 0 0.373 0.3672789 1.0000000 0.00000000 NA
5: 1 1 NA 0.2119940 0.5772017 -0.15528492 NA
6: 1 2 NA 0.5562891 1.5146230 0.18901019 NA
7: 2 0 0.513 0.5119456 1.0000000 0.00000000 0.0
8: 2 1 NA 0.2922588 0.5708787 -0.21968680 83.1
9: 2 2 NA 0.7138322 1.3943516 0.20188659 80.8
Aver % Intervened On
<num>
1: NA
2: NA
3: NA
4: NA
5: NA
6: NA
7: 0.00000
8: 49.96667
9: 46.93333
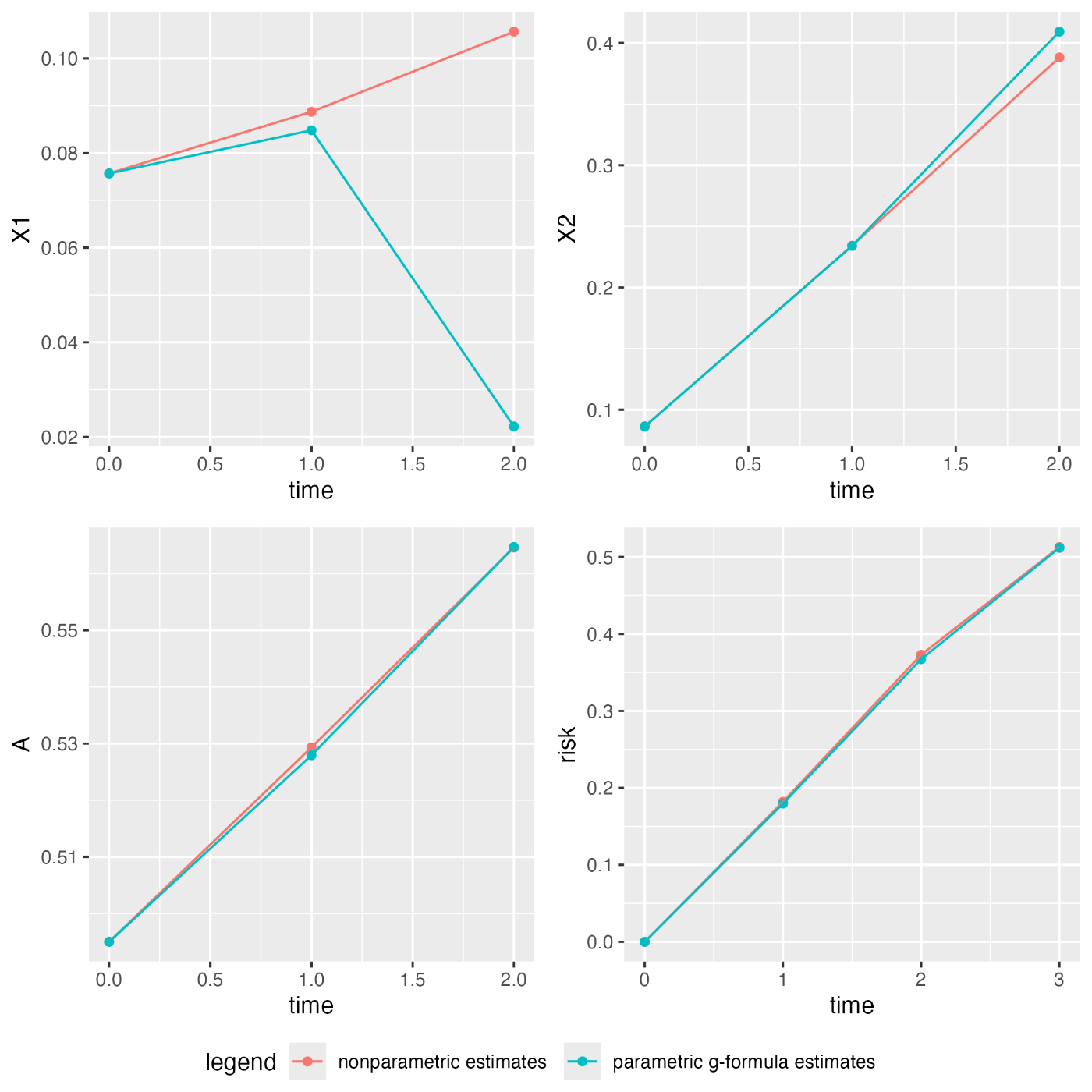
-
plot()を実行するとnatural courseにおけるnon-parametricとparametricの違いを見ることができる。natural courseは治療レジメンを変更しなかった場合の軌跡のことで、parametric natural courseは今回仮定しているparametric g-formulaのモデルを用いた場合のnatrural courseのことで、non-parametricは実データでの平均や割合を単純な集計によって推定しているものと思われる。 - riskのグラフだけデータセットで設定したtime 0がtime 1になっていて、0始点にするために新たなtime 0ができているので注意する。
- X1はずれているように見えるが、そのほかのプロットはほぼ一致していた。これをもって実データ解析でもモデルの妥当性を主張することができるのかどうか、X1のずれの部分をどう捉えるべきなのかは悩ましい。
plot(gformula_fit)
ブートストラップ
- ブートストラップを追加することで信頼区間も得られた。自作よりもやはりかなり高速。
- 平均値は自作とほぼ同じであったが、CIについては1桁%ずれている。少し差が大きいのでもっとブートストラップの反復回数を増やした方がいいのかもしれない。
ncores <- parallel::detectCores() - 1
tic()
gformula_fit_boot <-
gformula(
outcome_type = 'survival',
obs_data = dt_gformula,
id = 'id',
time_name = 'time',
outcome_name = 'status',
covnames = c('X1', 'X2', 'A'),
histories = c(lagged),
histvars = list(c('X1', 'X2', 'A')),
covtypes = c('normal', 'normal', 'binary'),
covparams = covparams,
ymodel = ymodel,
time_points = 3,
intvars = list('A', 'A'),
int_descript = c('Never treat', 'Always treat'),
interventions = list(
list(c(static, rep(0, 3))),
list(c(static, rep(1, 3)))
),
nsimul = 1000,
seed = 1234,
parallel = TRUE,
nsamples = 10,
ncores = ncores)
toc()
7.275 sec elapsed
> gformula_fit_boot$result
k Interv. NP Risk g-form risk Risk SE Risk lower 95% CI
<num> <num> <num> <num> <num> <num>
1: 0 0 0.182 0.1796748 0.009448988 0.15755249
2: 0 1 NA 0.1160781 0.008764534 0.09765739
3: 0 2 NA 0.2682741 0.012055155 0.24292510
4: 1 0 0.373 0.3672789 0.011568998 0.34670406
5: 1 1 NA 0.2119940 0.015020882 0.18136511
6: 1 2 NA 0.5562891 0.007914926 0.54598413
7: 2 0 0.513 0.5119456 0.012586060 0.49585785
8: 2 1 NA 0.2922588 0.019252716 0.25345941
9: 2 2 NA 0.7138322 0.009604172 0.70376668
Risk upper 95% CI Risk ratio RR SE RR lower 95% CI RR upper 95% CI
<num> <num> <num> <num> <num>
1: 0.1859603 1.0000000 0.00000000 1.0000000 1.0000000
2: 0.1249570 0.6460458 0.03251060 0.5942731 0.6950618
3: 0.2803768 1.4931094 0.04254912 1.4408003 1.5575123
4: 0.3843831 1.0000000 0.00000000 1.0000000 1.0000000
5: 0.2281291 0.5772017 0.02656587 0.5212755 0.6066566
6: 0.5704133 1.5146230 0.04934905 1.4643815 1.6183965
7: 0.5345241 1.0000000 0.00000000 1.0000000 1.0000000
8: 0.3131160 0.5708787 0.02687886 0.5096248 0.5980622
9: 0.7308065 1.3943516 0.03709057 1.3536635 1.4662874
Risk difference RD SE RD lower 95% CI RD upper 95% CI % Intervened On
<num> <num> <num> <num> <num>
1: 0.00000000 0.000000000 0.00000000 0.00000000 NA
2: -0.06359665 0.006498321 -0.07447327 -0.05406735 NA
3: 0.08859932 0.006332216 0.07855352 0.09685416 NA
4: 0.00000000 0.000000000 0.00000000 0.00000000 NA
5: -0.15528492 0.006966884 -0.16868636 -0.14740312 NA
6: 0.18901019 0.012431653 0.17443438 0.21417820 NA
7: 0.00000000 0.000000000 0.00000000 0.00000000 0.0
8: -0.21968680 0.010435188 -0.24406874 -0.20985202 83.1
9: 0.20188659 0.014739772 0.18522805 0.23144484 80.8
Aver % Intervened On
<num>
1: NA
2: NA
3: NA
4: NA
5: NA
6: NA
7: 0.00000
8: 49.96667
9: 46.93333
自作とパッケージの中身の一致確認
モデルフィッティングの確認
- プールしたデータにフィッティングしたモデルは完全に一致していることを確認した。
> coef(gformula_fit)
$X1
(Intercept) lag1_A lag1_X1 lag1_X2
-0.006481349 0.207692433 0.997608575 -0.004530390
$X2
(Intercept) lag1_A lag1_X1 lag1_X2
0.004115335 0.199187377 -0.004468244 1.002809184
$A
(Intercept) lag1_A lag1_X1 lag1_X2
0.01737885 0.17661264 -0.49736577 0.53253964
$status
(Intercept) A lag1_A X1 X2 lag1_X1
-2.26882387 1.11872329 0.64910668 1.14300019 -0.37191443 -0.48910410
lag1_X2
-0.09074852
> coef(model_X1)
(Intercept) A_l1 X1_l1 X2_l1
-0.006481349 0.207692433 0.997608575 -0.004530390
> coef(model_X2)
(Intercept) A_l1 X1_l1 X2_l1
0.004115335 0.199187377 -0.004468244 1.002809184
> coef(model_Y)
(Intercept) A A_l1 X1 X2 X1_l1
-2.26882387 1.11872329 0.64910668 1.14300019 -0.37191443 -0.48910410
X2_l1
-0.09074852
使用しているデータの一致確認
-
gformula_fit$fits$X1$dataでフィッティングされたデータ全体を確認でき、gformula_fit$fits$X1$modelでモデルに使われたデータを確認できる。 - gformulaのMCサンプリングの反復回数がオリジナルのサンプルサイズと同じ時は、観測されたXの値をそのまま初回時点では使用する仕様になっている。
- 1:5行までだとtime=1しか確認ができないがX1, X2の値の一致を確認できる。
- 注意点は、{gfoRmula}ではモデルに含めたラグの次数に合わせてXのモデリングに使う時点が変わることである。今回はt>1のみが利用されているので、時点がずれている。また、id = 2は time = 1のデータしか元々存在しなかっったため{gfoRmula}のデータには存在しない。
> gformula_fit$fits$X1$data[1:5, ]
Key: <id>
id time X1 X2 A status X1_l1 X2_l1 A_l1
<int> <num> <num> <num> <num> <num> <num> <num> <num>
1: 1 1 1.0155902 0.6296745 0 0 0.7980722 0.2628903 1
2: 1 2 1.0075913 0.5951780 1 1 1.0155902 0.6296745 0
3: 3 1 1.1640449 3.0293096 1 1 0.9009379 2.9411965 1
4: 4 1 -0.6958211 0.5941237 0 0 -0.7241960 0.7422998 0
5: 4 2 -0.6690531 0.6167777 1 0 -0.6958211 0.5941237 0
lag1_X1 lag1_X2 lag1_A newid
<num> <num> <num> <int>
1: 0.7980722 0.2628903 1 1
2: 1.0155902 0.6296745 0 1
3: 0.9009379 2.9411965 1 3
4: -0.7241960 0.7422998 0 4
5: -0.6958211 0.5941237 0 4
# {gfoRmula}ではt>1を使うのでこのデータセットのtime=2がgformulaデータでのtime=1なので一致している。
> df_gformula[1:5, ]
id time X1 X2 A status X1_l1 X2_l1 A_l1
1 1 1 0.7980722 0.2628903 1 0 0.7207567 0.1356414 0
2 1 2 1.0155902 0.6296745 0 0 0.7980722 0.2628903 1
3 1 3 1.0075913 0.5951780 1 1 1.0155902 0.6296745 0
4 2 1 -1.5785631 -0.2143476 1 1 -1.6550540 -0.3209638 0
5 3 1 0.9009379 2.9411965 1 0 0.8337854 2.9527814 0
- アウトカムの方はtime=0からデータをモデリングに使用しているので一致確認はやりやすい。
> gformula_fit$fits$status$model[1:5,]
status A lag1_A X1 X2 lag1_X1 lag1_X2
1 0 1 0 0.7980722 0.2628903 0.7207567 0.1356414
2 0 0 1 1.0155902 0.6296745 0.7980722 0.2628903
3 1 1 0 1.0075913 0.5951780 1.0155902 0.6296745
4 1 1 0 -1.5785631 -0.2143476 -1.6550540 -0.3209638
5 0 1 0 0.9009379 2.9411965 0.8337854 2.9527814
生成データの確認
-
gfoRmula()を実行する際に、sim_data_b = TRUEとしておくと生成されたデータが残るので中身を確認できる。
head(gformula_fit$sim_data$`Always treat`)
id time X1 X2 A eligible_pt intervened lag1_X1
<int> <num> <num> <num> <num> <lgcl> <lgcl> <num>
1: 1 0 0.7980722 0.26289031 1 TRUE FALSE 0.7207567
2: 1 1 0.9970083 0.17823385 1 TRUE FALSE 0.7980722
3: 1 2 1.1825142 0.28682885 1 TRUE FALSE 0.9970083
4: 2 0 -1.5785631 -0.21434755 1 TRUE FALSE -1.6550540
5: 2 1 -1.3133551 0.08916744 1 TRUE TRUE -1.5785631
6: 2 2 -1.0335129 0.37327747 1 TRUE TRUE -1.3133551
lag1_X2 lag1_A Py Y D prodp1 prodp0 poprisk
<num> <num> <num> <int> <num> <num> <num> <num>
1: 0.13564140 0 0.3316990 0 0 0.3316990 0.6683010 0.3316990
2: 0.26289031 1 0.5394433 1 0 0.3605105 0.3077905 0.6922095
3: 0.17823385 1 0.5597454 0 0 0.1722843 0.1355062 0.8644938
4: -0.32096376 0 0.1154687 0 0 0.1154687 0.8845313 0.1154687
5: -0.21434755 1 0.2237773 1 0 0.1979380 0.6865933 0.3134067
6: 0.08916744 1 0.2338226 0 0 0.1605410 0.5260523 0.4739477
survival
<num>
1: 0.6683010
2: 0.3077905
3: 0.1355062
4: 0.8845313
5: 0.6865933
6: 0.5260523
# 自作gformulaで利用したデータの中身の一部
> head(df_sim_gformula %>%
filter(hypo_interv == "Always treated"))
hypo_interv id time A_l1 A status at_risk hazard X1 X2
1 Always treated 1 1 0 1 0 1 0.3775870 0.7980722 0.26289031
2 Always treated 1 2 1 1 1 1 0.4834876 0.9181284 0.24856530
3 Always treated 1 3 1 1 0 0 0.5203826 1.0947756 0.55239309
4 Always treated 2 1 0 1 1 1 0.1378037 -1.5785631 -0.21434755
5 Always treated 2 2 1 1 0 0 0.1696942 -1.2386679 -0.08744384
6 Always treated 2 3 1 1 0 0 0.2785680 -1.0114323 0.14723566
X1_l1 X2_l1 sim_n
1 0.7207567 0.13564140 1
2 0.7980722 0.26289031 1
3 0.9181284 0.24856530 1
4 -1.6550540 -0.32096376 1
5 -1.5785631 -0.21434755 1
6 -1.2386679 -0.08744384 1
まとめ
- 時間依存性治療でtime-to-eventデータにおけるg-formulaの自作と、その{gfoRmula}との一致を確認した。
- 概ね実装として問題ないgformulaの自作を行うことができたが、ブートストラップに関しては疑問も残るため、モンテカルロシミュレーションのサンプリング数を減らしてブートストラップのリサンプリング数を増やすなどの対応をした方がいいのかなども含めて、トイデータで確認できると良いと考えている。
- {gfoRmula}ではラグ次数に応じて共変量モデリングにおいて使うデータを制限しているが、prebaseline情報がある場合にはこの制限を外してもよいように思うので、その違いの影響なども検証してみたい。
- ブートストラップのややこしさを考えると、やはりベイズ的にやった方が自然な結果を得られるような気がするため、ベイズでの実装もチャレンジしたい。
Discussion