Zenn
🖼️

ふんわり理解するGrad-CAM

2022/03/12に公開
TensorFlow
ディープラーニング
gradcam
tech

画像を入力としたモデルの局所的説明性を得る手法の1つであるGrad-CAMという手法について説明します。
論文：Grad-CAM: Visual Explanations from Deep Networks via Gradient-based Localization (ICCV オープンアクセス版) (arxiv版)

Grad-CAMってなあに


論文 fig1 より一部抜粋

深層学習ではモデルの予測が何を根拠に判断されているかが分からないという問題があります。Grad-CAMはCNNベースの画像認識モデルに対してある入力とその予測に対して局所的な説明を与える手法です。上の画像のようにある入力画像に対して画像のどの部分が予測に最も影響を与えたかをヒートマップとして出力することで個々の予測に対する視覚的説明を得ます。

視覚的説明の拠り所

ハイライトによる視覚的説明（なぜハイライトした部分がモデルが予測のために注目したと言えるのか）の根拠はClass Activation Mapping(CAM)をもとにしています。

Class Activation Mapping(CAM)について

CAMはCNNが位置情報を保持したまま特徴量を抽出できていることを用いて特徴量マップから画像のどこの部分が予測に影響を与えたかを計算します。

画像のクラス分類のタスク[1]を考えます。 クラス予測のモデルを
入力層→畳み込み、プーリング層→Global Average Pooling(GAP)層→出力層（ソフトマックス関数）

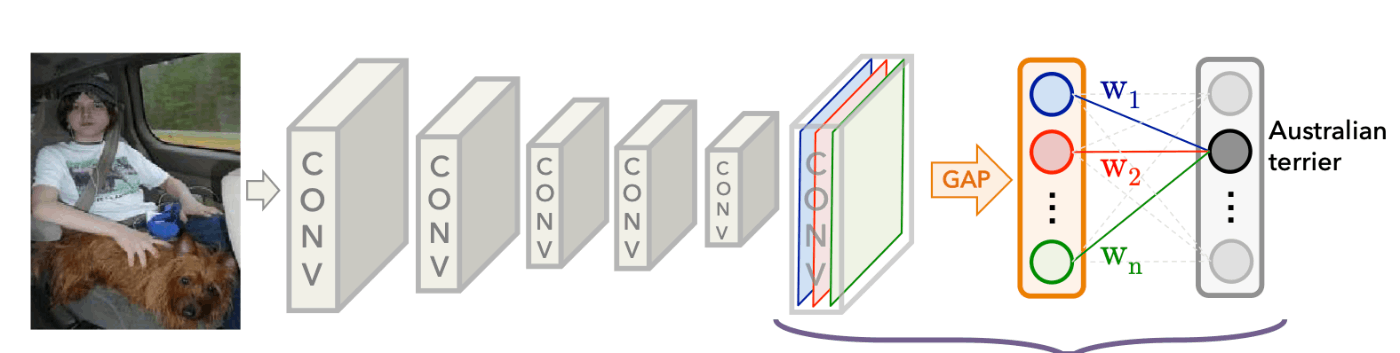
CAMの論文 fig2

とします。ここで入力画像ベクトルを\mathbf{I}, GAP層の前の畳み込み層の出力をk枚目の特徴量マップの位置x,yについてA^k_{xy}, 特徴量マップの要素数をZ, GAP層と出力層をつなぐ重みをw^k_c, クラスcについての出力層の値をS_c とする。


数式と対応させるためのモデルの概念図

あるクラスcについての出力は下のように計算される。

S_c = \sum_k w^k_c \underbrace{\frac{1}{Z}\sum_{x,y}A^k_{xy}}_{\text{grobal average pooling}}

ここで単純な積の計算は入れ替えられるので

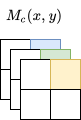
S_c = \frac{1}{Z} \sum_{x,y} \sum_k w^k_c A^k_{xy} \\ S_c = \frac{1}{Z}\sum_{x,y} M^c_{\text{CAM}}(x,y)


Mcはfeature mapのある位置x, yに基づいて計算されるので位置情報を保持している

（ただしM^c_{\text{CAM}}(x,y) = \sum_k w^k_c A^k_{xy}とまとめただけ。）ここでS_cはM_cによって計算され、またS_cはクラスの確率であるため大きければ大きいほどそのクラスであると判断されます。よって全ての位置x, yについてM^c_{\text{CAM}}(x,y)をみた時に値が大きければ大きいほどその位置x, yが予測に良い影響を与えたということになります。
このようにしてCAMでは視覚的説明のためのヒートマップを計算します。ただし問題点としてモデルにある程度制約がかかってしまいます。

CAMからGrad-CAMへ

Grad-CAMはCAMによるヒートマップの計算をモデルの制約に囚われないよう一般化したものです。
具体的にはCAMでのM^c_{\text{CAM}}(x,y)の計算においてw^k_c の代わりに\alpha^k_c = \frac{1}{Z}\sum_{x,y} \frac{\partial S_c}{\partial A^k_{xy}}を使えることを示しました。（ CAMの時の計算式(S_c = \sum_k w^k_c \frac{1}{Z}\sum_{x,y}A^k_{xy})で両辺偏微分したりいじったりしてると得ることができます。[2]）

M^c_{\text{Grad-CAM}}(x,y)=\sum_k \alpha^k_c A^k_{xy}

ここでGrad-CAMのヒートマップの計算のために必要なのは出力に対する特徴量マップの値の勾配であり、これは深層学習モデルでは任意のモデルで計算可能であるためモデルの制約の問題が解決されました。

ReLU関数による正の寄与度の抽出

Grad-CAMではCAMの時と違いヒートマップを算出する際にReLU関数を通すことで正の値のみを抽出しています。

M^c_{\text{Grad-CAM}}(x,y)=ReLU \left( \sum_k \alpha^k_c A^k_{xy} \right)

これはクラス分類のタスクを考えた時（ここでは特にクラス分類のタスクを考える）画像のある部分がそのクラスであるために正の寄与を与えたということが負の寄与よりも特に重要であることからこのような処理をほどこしています。

まとめと議論

まとめるとGrad-CAMではヒートマップを以下のように計算します。

M^c_{\text{Grad-CAM}}(x,y)=ReLU \left( \sum_k \alpha^k_c A^k_{xy} \right) \\ \alpha^k_c = \frac{1}{Z}\sum_{x,y} \frac{\partial S_c}{\partial A^k_{xy}}

勾配を使うことでCAMの理論に基づいて任意のCNNモデルでヒートマップを計算できるようになりました。しかし得られるヒートマップや説明性に対する評価がしにくい（説明に正解がないので）、妥当性が得づらいなどの課題が残りよく議論[3]されています。（これはGrad-CAMだけに限らず説明性手法全般に言えますが）

Grad-CAMの実装

実装はライブラリが揃ってるので雑にそれらを使うのもいいですがせっかくなので中まで覗いて写経するなり自分なりに実装するなりしておくと勉強になります。

参考コード：Keras documentation: Grad-CAM class activation visualization

def make_gradcam_heatmap(img,model,target_layer_name,pred_index=None):
    grad_model = tf.keras.Model(
        [model.inputs],[model.get_layer(target_layer_name).output,model.output]
    )
    
    with tf.GradientTape() as tape:
        target_layer_output, preds = grad_model(img)
        if pred_index is None:
            pred_index = tf.argmax(preds[0])
        class_channel = preds[:,pred_index]
    
    grads = tape.gradient(class_channel,target_layer_output)
    pooled_grads = tf.reduce_mean(grads,axis=(0,1,2)) # αの計算
    
    heatmap = target_layer_output[0] @ pooled_grads[...,tf.newaxis] # α * A^k
    heatmap = tf.squeeze(heatmap)
    
    # ReLU and normalize
    heatmap = tf.maximum(heatmap, 0) / tf.math.reduce_max(heatmap)
    
    return heatmap.numpy()

実装コードのリポジトリ
https://github.com/mfmf-gaupon/zenn-article-code/tree/main/ふんわり理解するGrad-CAM

Open In Colab モデルの予測からgrad-camによる可視化の一連の流れを確認できます。

その他参考文献

脚注

  1. 必ずしもクラス分類のタスクである必要はない ↩︎

  2. 詳細な計算はarxiv版論文に載ってるので割愛 ↩︎

  3. 画像を使った視覚的説明手法では説明の信頼性の議論、批判はよくなされている。（例えば Sanity Checks for Saliency Maps で重みをランダムにしてもヒートマップがほとんど変化しない≒モデルの説明性になっていないなど） ↩︎

Discussion