python覚えたい+財務分析
- Pythonを覚えたい。
- 三日坊主防止の為、株取引を目標に何か作りながら覚えたい。
- プログラミング自体は実務経験あるので、自分のメモ程度の内容になる。
- ついでにMarkdownにも慣れたい。(LaTeXなら学生時代触ったことがある。)
- いずれ記事や本にまとめたい。
- データ収集元案:EDINET、日本銀行、企業HP等
- 参考文献:
- 経営分析―会計データを読む技法(2007)
- 太田浩司の会計・ファイナンスホームページ「企業財務論」(アクセス:2022/03/17)
- 新・証券投資論[Ⅰ] ―理論編―(2009)
- 新・証券投資論[Ⅱ] ―実務編―(2009)
- 2022年版EDINETタクソノミの公表について:金融庁 - 3.公表資料:勘定科目リスト(アクセス:2022/03/18)
- 会計用語集
- 証券用語解説集|野村證券
- EDINET
資本利益率(ROE:return on equity)
-
利益:r
-
資本:e
-
モデル:
ROE = \dfrac{r}{e} -
目安:一般的に、10〜20%であれば優良企業。
#資本利益率
def roe(r, e):
return 0 if e == 0 else r/e
#ROE評価関数
def evaROE(val):
return "超優良" if val >= 0.2 else "優良" if val >= 0.1 else "劣"
#--------------------------------------------
# 主処理
def main():
profit = 100 #利益
equity = 5000 #資本
rate = roe(profit, equity)
print("利益 = " + str(profit) )
print("資本 = " + str(equity) )
print("資本利益率 = " + str(rate) )
print("評価 = " + evaROE(rate) )
#--------------------------------------------
# 実行
print("===========" + "開始" + "===========")
main()
print("===========" + "終了" + "===========")
実行結果
===========開始===========
利益 = 100
資本 = 5000
資本利益率 = 0.02
評価 = 劣
===========終了===========
roe関数及びevaROE関数では、returnに直接式を書いて結果を返すようにした。
今回は通常のif文を使わずに、三項演算子により記述量を減らしてみた。
評価方法は、比率が20%以上なら超優良、10%以上なら優良、10%未満なら劣。
値1 if 条件式1 else 値2
この場合、
条件式1が真ならば、結果は値1となる。
条件式1が偽ならば、結果は値2となる。
値1 if 条件式1 else 値2 if 条件式2 else 値3
「三項演算子1」の値2の場所に更に3項演算子をネストできるらしい。
これにより条件式1が偽の時、値2つまり条件式2の判定を行う。
したがって三項演算子2では、
条件式1が真ならば、値1となる。
条件式1が偽ならば、条件式2となる。
条件式2が真ならば、値2となる。
条件式2が偽ならば、値3となる。

貸借対照表

損益計算書
- 財務諸表の表記方法:勘定式と報告式がある。
| 損益計算書(報告式) | ||
|---|---|---|
| 営業損益計算 | Ⅰ. 売上高 | |
| Ⅱ. 売上原価 | ||
売上総利益 |
||
| Ⅲ. 販売費および一般管理費 | ||
営業利益 |
||
| 経常損益計算 | Ⅳ. 営業外収益 | |
| Ⅴ. 営業外費用 | ||
経常利益 |
||
| 純損益計算 | Ⅵ. 特別利益 | |
| Ⅶ. 特別損失 | ||
税引前当期純利益 |
||
| 法人税等 | ||
| 法人税等調整額 | ||
当期純利益 |
||
| 未処分損益計算 | 前期繰越利益 | |
| 任意積立金取崩額 | ||
| 中間配当額 | ||
| 利益準備金積立額 | ||
当期未処分利益 |
貸借対照表

負債(他人資本)+資本(自己資本):資金の調達源泉
資産:資金の運用形態
太田浩司の会計・ファイナンスホームページ「企業財務論」
| 用語 | 英訳 |
|---|---|
| 総資本 | total capital |
| 事業利益 | business interests |
| 資本事業利益率(総資産事業利益率) | ROA:Return on Assets |
収益性の分析
太田浩司の会計・ファイナンスホームページ「企業財務論」(8章)
資本利益率(ROE:return on equity)
- 企業の収益性は、財務分析で一番重要な視点で、その指標が資本利益率。
- 同じ売上高、同じ利益の企業同士を比較する時、元手(資本)に対する利益で評価できる。
ROE = \dfrac{利益}{資本}
- 目安:一般的に、10〜20%であれば優良企業。
- 3種
- 総資本事業利益率
- 経営資本営業利益率
- 自己資本当期純利益率
1. 総資本事業利益率
- 総資産事業利益率(ROA)と等価
ROA = \dfrac{事業利益}{総資本} \text{総資本}=\text{他人資本}+\text{自己資本} \text{事業利益}=\text{営業利益}+\text{自己資本}
2. 経営資本営業利益率
-
\text{経営資本営業利益率} = \dfrac{\text{営業利益}}{\text{経営資本}} - 経営資本:
- 企業本来の営業活動に投下された資本。
- 総資本から企業本来の営業活動に投下されていない資本を引く。
- ①流動資産のうち「現金預金、有価証券、短期貸付金」
- ②固定資産のうち「投資その他の資産」
- ③有形固定資産のうち「建設仮勘定」
- ④繰延資産
経営資本 = 総資本 - (① + ② + ③ + ④)
- 営業利益:企業本来の営業活動から得られた利益。
3. 自己資本純利益率
- 自己資本純利益率:株主観点で、株主が出資金額に対する収益性を分析する指標。
自己資本純利益率 = \dfrac{当期純利益}{自己資本}
- 自己資本:株主資本
- 当期純利益:最終的に株主に帰属する利益。
- 自己資本利益率(ROE:Return on Equity)
資本利益率の分解
\begin{align*} 資本利益率 &= \dfrac{利益}{資本} \\\\ &= \dfrac{利益}{売上高}\cdot\dfrac{売上高}{資本} \\\\ &= 売上高利益率 \times 資本回転率 \end{align*}
- 資本利益率は、「加算される付加利益(売上高利益率)」の大きさと「その営業循環を年に何回繰り返す(資本回転率)」によって決定する。
総資本事業利益率(ROA)と自己資本利益率(ROE)の分解
1. ROAの分解
- 総資本事業利益率(ROA)の2つの指標:売上高純利益率、総資本回転率。
ROA = \dfrac{事業利益}{売上高} = \dfrac{売上高}{総資本}
2. ROEの分解
- 自己資本純利益率(ROE)の3つの指標:売上高純利益率、総資本回転率、財務レバレッジ。
- デュポン・システムと呼ばれる。
ROE = \dfrac{利益}{資本} = \dfrac{当期純利益}{売上高}\cdot\dfrac{売上高}{総資本}\cdot\dfrac{総資本}{自己資本}
- 財務レバレッジ:定義は多数あるが、いずれも分母に自己資本を用いる。
\begin{aligned}財務レバレッジ= \dfrac{総資本}{自己資本} \\\\ or \space \space \space \space 財務レバレッジ = \dfrac{負債}{自己資本} = \dfrac{他人資本}{自己資本} \end{aligned}
3. ROAとROEの関係
ROE = \{ ROA + (ROA - 負債利子率 \cdot\dfrac{負債}{自己資本}) \}\cdot(1 - 法人税率)
- ROEの向上:
- ROA>負債利子率の時、財務レバレッジを上げる
- ROA<負債利子率の時、財務レバレッジを下げる
損益計算書
- 営業損益計算
- 売上総利益:粗利益
売上総利益 = 売上高 - 売上原価
\begin{aligned} 売上総利益率 = \dfrac{営業利益}{売上高}\\\\ または、 \dfrac{売上高-売上原価}{売上高} \end{aligned}
営業利益 = 売上総利益 - 販売費及び一般管理費
売上高営業利益率 = \dfrac{営業利益}{売上高}
- 経常損益計算
- 本来の営業活動以外から生じた損益。
- 毎期経常的・反復的に発生する営業外利益。
企業の正常収益力を表す。
経常利益 = 営業利益 + 営業外収益
売上高経常利益率 = \dfrac{経常利益}{売上高}
- 純損益計算
- 当期純利益。
税引前当期純利益 = 経常利益 \pm 特別利益
当期純利益 = 税引前当期純利益 - 法人税等
売上高当期純利益率 = \dfrac{当期純利益}{売上高}
自己資本当期純利益率 = \dfrac{当期純利益}{自己資本}
- 未処分損益計算
- 当期未処分利益(Unappropriated income at end of term)は、処分可能利益を表す。
- ①当期純利益(profit)
- ②前期繰越利益(Balance brought forward)
- ③任意積立金取崩額(Reversal of voluntary retained earnings)
- ④中間配当額(Interim dividends paid)
- ⑤中間配当に伴う利益準備金積立額(Legal reserve of retained earnings for interim dividends)
当期未処分利益 = ① + ② + ③ - ④ - ⑤
- 金融収益・費用
- 金融収益:企業の財務・金融活動から得られらた収益。
金融収益 = 受取利息 + 受取配当金 + 有価証券利息
- 金融費用:企業の資金調達活動によって生じた費用。
金融費用 = 支払利息 + 支払割引料 + 社債利息
- 事業利益
- 事業絶対の成果を表す利益。
事業利益 = 営業利益 + 金融収益
総資本事業利益 = \dfrac{事業利益}{総資本}
- 利払後事業利益
利払後事業利益 = 事業利益 - 金融費用
貸借対照表
- 経営資本
- 企業本来の経営活動のために利用する資本。
経営資本 = 総資産 - 財務活動資産 - 建設仮勘定 - 繰延資産
財務活動資産 = 預金 + 有価証券 + 短期貸付金 + 投資その他の資産
収益性の分析2
太田浩司の会計・ファイナンスホームページ「企業財務論」(9章)
その他の指標
- 売上高金融費用比率
売上高金融費用比率 = \dfrac{金融費用}{売上高}
- インスタント・カバレッジ・レシオ
インスタント・カバレッジ・レシオ = \dfrac{営業利益 + 受取利息+配当金}{支払利息+割引料等}
資本効率の分析
- 資産回転率
- 投下資本が年間で売上として何回回収されたかを示す指標。
資産回転率(回) = \dfrac{売上高}{資産}
資産回期間(月) = \dfrac{12ヶ月}{資産回転率}
資産回日数(日) = \dfrac{365日}{資産回転率}
- 売上債権回転率
- 売上債権の回収状況を示す指標
売上債権回転率(回) = \dfrac{売上高}{売上債権の期首及び期末平均残高}
売上債権 = 売掛金 + 受取手形 + 割引手形
- 棚卸資産回転率
- 棚卸資産の在庫期間を表す指標で,回転率が高いほど企業の販
売力が高い。
棚卸資産回転率(回) = \dfrac{売上高}{棚卸資産の期首及び期末平均残高}
- 有形固定資産回転率
- 設備投資に対する収益力の良否を表す指標。
有形固定資産回転率(回) = \dfrac{売上高}{有形固定資の期首及び期末平均残高}
- 手元流動性比率
- 企業が即時に支払うことができる資金である,流動資産の現金
預金と有価証券の合計額が,平均月商の何月分であるかを表す指標。
手元流動性比率(月) = \dfrac{(現金預金 + 有価証券)の期首及び期末平均残高}{(年間売上高\div12ヶ月)}
付加価値分析
- 付加価値の計算
- 企業が購入した材料などの中間財(中間生産物)に対して,新たに生み出した価値額。
- 付加価値の計算方法2つ。
- 控除法
付加価値=総生産高-前給付費用(中間生産物) - 加算法
付加価値=人件費+減価償却費+賃借料+租税公課+他人資本利子+税引後純利益
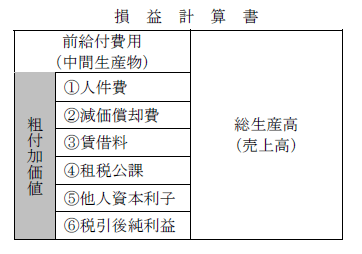
損益計算書
- 前給付費用(中間生産物)
- 総生産高(売上高)
- 粗付加価値:
①人件費
②減価償却費
③賃借料
④租税公課
⑤他人資本利子
⑥税引後純利益
- 労働生産性の分析
- 従業員一人当りの付加価値額であり,人的資源の観点からみた生
産性の指標。
労働生産性 = \dfrac{付加価値額}{平均従業員数}
-
労働生産性の分解
- 売上高との関連で「付加価値率」と「従業員一人当りの売上高」に分解。
\begin{align*}\dfrac{付加価値額}{平均従業員数} &= \dfrac{付加価値額}{売上高}\cdot\dfrac{売上高}{平均従業員数} \\\\ &= 付加価値率 \times 1人当り売上高 \end{align*} - また有形固定資産との関連で「設備生産性」と「労働装備率」に
分解。
\begin{align*}\dfrac{付加価値額}{平均従業員数} &= \dfrac{付加価値額}{有形固定資産}\cdot\dfrac{有形固定資産}{平均従業員数} \\\\ &= 設備生産性 \times 労働装備率 \end{align*}
- その他の生産性の分析
- 従業員一人当り人件費:
\begin{align*} 一人当り人件費 &= \dfrac{人件費}{平均従業員数} \\\\ &= \dfrac{人件費}{付加価値額}\cdot\dfrac{付加価値額}{平均従業員数} \\\\ &= 労働分配率 \times 労働生産性 \end{align*}
- 労働分配率:付加価値に占める人件費の割合。
労働分配率 = \dfrac{人件費}{付加価値額}
- 設備生産性:設備が付加価値の産出にどの程度貢献しているかをみる指標。
設備生産性 = \dfrac{付加価値額}{有形固定資産}
- 資本生産性:使用総資本がどの程度付加価値の産出に寄与しているかをみる指標。
資本生産性 = \dfrac{付加価値額}{総資本}
財務安全性の分析
太田浩司の会計・ファイナンスホームページ「企業財務論」(10章)
静態的安全性分析
- 財務安定性:
- 短期的な支払能力の分析:流動比率、当座比率
- 資金調達の構成を分析:負債比率、自己資本比率
- 長期資金と固定資産への運用の関係を分析:固定比率、固定長期適合率
- 流動比率と当座比率
-
短期的な財務安全性(債務返済能力)の分析指標2つ。
-
流動性比率:
- 運転資本である流動資産を処分して、短期的(一年以内)に支払わ
ねばならない流動負債を返済できるかどうかを表す指標。 - 目安:200%
流動性比率 = \dfrac{流動資産}{流動負債} - 運転資本である流動資産を処分して、短期的(一年以内)に支払わ
-
当座比率:
- 流動資産の中で換金性の低い棚卸資産(商品、製品、仕掛品)を除いた当座資産のみを支払手段として、短期的(一年以内)に支払わねばならない流動負債を返済できるかどうかを表す指標。
- 目安:100%
当座比率 = \dfrac{当座資産}{流動負債} 当座資産 = 現金預金 + 売上債権(受取手形や売掛金)+短期有価証券
- 負債比率と自己資本比率
- 長期的な財務安全性(債務返済能力)の分析指標。
- 負債比率:
- 比率が大きいほど財務リスクが大きい。
負債比率 = \dfrac{他人資本}{自己資本} - 自己資本比率(株主資本比率):
- 他人資本の安全度を見る指標。
- 自己資本は返済を必要としない資本であるから、自己資本比率が高いほど他人資本への返済担保力が大きい。
自己資本比率 = \dfrac{自己資本}{自己資本+他人資本}
- 固定費率と固定長期適合率
- 長期的な観点から企業の財務安全性(債務返済能力)を分析するもう一つの方法。
- 長期的な資金運用が短期的な資金調達によってなされていないかどうかを分析す
る方法。 - 固定比率と固定長期適合率の2つ。
- 固定比率:
- 設備投資は返済の必要のない自己資本で賄われるべきであるとする考え方。
- 目安:100%。
固定比率 = \dfrac{固定資産}{自己資本} - 固定長期適合率:
- 設備投資は返済の必要のない自己資本で賄われるべきであるが、それを超過する分は少なくとも、社債・長期借入金といった固定負債で賄われるべきであるとする考え方。
固定長期適合率 = \dfrac{固定資産}{自己資本+固定負債}
損益分岐点分析
- 費用を変動費及び固定費に分解して、その費用構造の観点から、利益に及ぼす財務安全性を評価する方法。
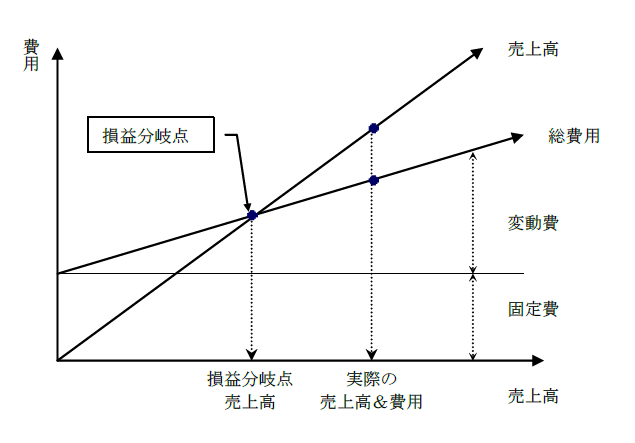
- 損益分岐点の意味
- 損益分岐点(Break Even Point: BEP):
- 損失も利益もでない損益の分かれ目、すなわち「総収益(売上高)-総費用=0」となる点。
- 損益ゼロの点における損益とは、営業利益を意味する。
-実際の損益計算書から損益分岐点分析を行う場合には、「売上原価」と「販売費及び一般管理費」を変動費と固定費に分解して、営業利益がゼロになる、損益分岐点売上高を算定する。

- 損益分岐点売上高の計算
\begin{align*} 損益分岐点売上高 &= \dfrac{固定費}{1-\dfrac{実際変動費}{実際売上高}} \\\\ &= \dfrac{固定費}{1-変動費率} \end{align*}
- 損益分岐点率と安全余裕率
- 損益分岐点比率:
- 実際の売上高に占める損益分岐点売上高の比率。
- 比率が小さいほど安全度が高い。
損益分岐点比率 = \dfrac{損益分岐点売上高}{実際の売上高} - 安全余裕率:
- 実際の売上高が損益分岐点売上高と比較してどの程度上回っているか(余裕度)を示す指標。
- 比率が大きいほど安全度が高い。
安全余裕率 = \dfrac{実際の売上高-損益分岐点売上高}{実際の売上高}
成長性の分析
太田浩司の会計・ファイナンスホームページ「企業財務論」(11章)
成長性の指標
- 株主観点:利益の成長性を重視。
一株当り利益の推移
- 利益総額の成長性を分析する。
- 一株当り利益(EPS: Earnings Per Share)
- 時系列で値を見る。
EPS = \dfrac{当期純利益}{発行済株式数}
- 一株当り利益の要因分解
\begin{align*} EPS &= \dfrac{当期純利益}{発行済株式数} \\\\ &= \dfrac{自己資本}{発行済み株式数}\cdot\dfrac{当期純利益}{自己資本} \\\\ &= BPS \times ROE \end{align*}
BPS:一株当り純資産
ROE:自己資本純利益率
- 潜在株式調整後一株当り利益
- 潜在株式調整後一株当り利益(完全希薄化後EPS)とは、潜在株式(転換社債、ワラント)が利権行使され、株式が発行されたとした場合の一株当り利益。
潜在株式調整後EPS = \dfrac{当期純利益\pm利益調整}{発行済株式数+潜在株式数}
- 転換社債:
当期純利益 += 転換に伴う金利負担軽減額(税引後) 発行済株式数 += 転換株数
- ワラント:
発行済株式数 += 未行使株数\cdot\dfrac{時価 - 行使価格}{時価}
- 希薄効果がない潜在株式(転換するとEPSが増加する転換社債、行使価格が時価を下回っているワラント)は除外する。
株式分割調整後の一株当り利益
- EPSを時系列で比較することは、その企業の成長性を判断する尺度となるが、株式分割が行われている場合には、単純な時系列比較はできない。
- このような希薄化に対して調整を行う。
- 株式分割がある場合の時系列比較
- 株式分割では、株式を無償交付するため株式数が増加するのみ、純資産は増加しないので、EPSを遡及修正計算する必要がある。
| 当期純利益 | 発行済み株式数 | EPS | |
|---|---|---|---|
| R1年3月期 | 120円 | 40株 | 3.0円 |
| R2年3月期 | 120円 | 48株 | 2.5円 |
| R3年3月期 | 120円 | 60株 | 2.0円 |
(資本異動)
R1年4月1日:1株に対して1.2株の分割
R2年4月1日:1株に対して1.25株の分割
<<遡及修正>>
R1年3月期の修正発行済み株式数:40 x 1.2 x1.25 = 60株
R2年3月期の修正発行済み株式数:48 x 1.25 = 60株
R3年3月期の修正発行済み株式数:60株
| 当期純利益 | 発行済み株式数 | EPS | |
|---|---|---|---|
| R1年3月期 | 120円 | 60株 | 2.0円 |
| R2年3月期 | 120円 | 60株 | 2.0円 |
| R3年3月期 | 120円 | 60株 | 2.0円 |
- 公募増資や合併がある場合の時系列比較
- 株式の有償交付である公募増資や合併では、株式数の増加に伴って純資産も増加するので、EPSを遡及修正計算する必要はない。
- 株式分割と公募増資がある場合の時系列比較
| 当期純利益 | 発行済み株式数 | EPS | |
|---|---|---|---|
| R1年3月期 | 120円 | 40株 | 3.0円 |
| R2年3月期 | 120円 | 48株 | 2.5円 |
| R3年3月期 | 120円 | 60株 | 2.0円 |
(資本異動)
R1年4月1日:公募(時価発行)によって8株を発行
R2年4月1日:1株に対して1.25株の分割
<<遡及修正>>
R1年3月期の修正発行済み株式数:40 x 1.25 = 50株
R2年3月期の修正発行済み株式数:48 x 1.25 = 60株
R3年3月期の修正発行済み株式数:60株
| 当期純利益 | 発行済み株式数 | EPS | |
|---|---|---|---|
| R1年3月期 | 120円 | 50株 | 2.4円 |
| R2年3月期 | 120円 | 60株 | 2.0円 |
| R3年3月期 | 120円 | 60株 | 2.0円 |
重要な投資指標
- 株価収益率(PER:Price-Earnings Rato)
- 株価が一株あたり利益の何倍になっているかを表す指標。
PER = \dfrac{株価}{一株当たり利益}
- 株価純資産倍率(PBR:Price-Book value Rato)
- 株価が一株あたり純資産額の何倍になっているかを表す指標。
PBR = \dfrac{株価}{一株当たり純資産}
- 配当利回り
- 株式への投資に対する配当の比率を表す指標。
配当利回り = \dfrac{一株当たり配当}{株価}
株式の基礎
太田浩司の会計・ファイナンスホームページ「企業財務論」(12章)
株式の投資収益率
株式の投資収益率
- インカム・ゲイン:配当
- キャピタル・ゲイン:株価の値上がり益
投資時点から1年後に配当を受取、直ちに売却した場合
r= \dfrac{D_1}{P_0} + \dfrac{ P_1 - P_0}{P_0}
:株式投資収益率 r :投資時点の株価 P_0 :売却時点の株価 P_1 :配当額(インカム・ゲイン) D_1
株式分割のある投資収益率
- 投資期間中に株式分割が行われた場合、投資収益率の計算には売却時の株数が増加していることを考慮しなければならない。
投資時点から1年後に配当を受取、直ちに売却した場合
r= \dfrac{D_1}{P_0} + \dfrac{ (1+a)P_1 - P_0}{P_0}
:1株に対する新株の割当比率 a
株式の投資尺度
株価収益率(PER: Price-Earnings Ratio)
- 株価を1株当り純利益(EPS: Earnings Per Share)で割った値。
- 一般に、PERの低い銘柄程割安、高い銘柄程割高。
PER = \dfrac{株価}{1株当たり利益}
株価純資産場率(PBR: Price-Book value Rate)
- 株価を一株当り純資産(BPS: Book value Per Share)で割った値。
- 一般に、PBRの低い銘柄程割安、高い銘柄程割高。
PBR = \dfrac{株価}{1株当たり純資産}
配当利回り
- 一株当たりの配当を株価で割った値
- 投資家の期待収益率の一部を表す
配当利回り = \dfrac{1株当たり配当} {株価}
益利回り
- EPSを株価で割った値
- PERの逆数
益利回り = \dfrac{EPS} {株価} = \dfrac{1} {PER}
イールド・スプレッド
- 債券利回りと益利回りの差をとったもの
- 株式相場の水準が長期国債と比較して割安割高を判断する指標
- 通常、正の値をとる。
- 値が小さくなるほど、株価の割安感が強くなる
イールド・スプレッド = 長期国債利回り - 益利回り
トービンのq
トービンのq = \dfrac{発行済株式数の時価総額 - 負債時価総額}{資産時価総額}
一般に、
- q<1:株価割安
- q=1:株価適正
- q>1:株価割高
配当割引モデル(DDM)
太田浩司の会計・ファイナンスホームページ「企業財務論」(13章)
- 配当割引モデル(DDM:Dividend Discount Model)
株式投資によって得られる将来キャッシュ・フローは配当であるので、株式の本質的価値(intrinsic value)は将来支払われる配当の現在価値の合計であるとする株式評価モデルである。
また、本質的価値は内在価値とも呼ばれ、一般に、理論株価と同義である。
定額配当割引モデル
- 毎年一定の配当額が支払われると仮定したDDM。
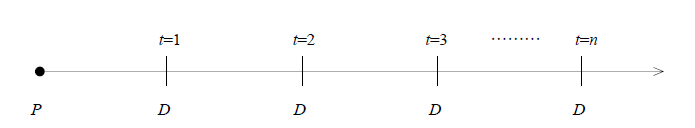
\begin{align*} P &=\dfrac{D}{(1+r)} + \dfrac{D}{(1+r)^2} + \dfrac{D}{(1+r)^3} + \cdots + \dfrac{D}{(1+r)^n} \\\\ &= \dfrac{D}{r} \end{align*}
:期間 t :現在価値 P :一定の将来配当額 D :投資家の期待収益率 r
定率成長配当割引モデル
- 毎年一定の割合で配当額が成長すると仮定したDDM。
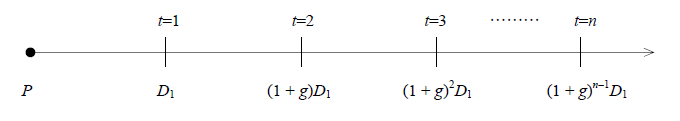
\begin{align*} P &=\dfrac{D_1}{(1+r)} + \dfrac{(1+g)D_1}{(1+r)^2} + \dfrac{(1+g)^2D_1}{(1+r)^3} + \cdots + \dfrac{(1+g)^{n-1}D_1}{(1+r)^n} \\\\ &= \dfrac{D_1}{(r-g)} \space \space \space \space \space \space \space \space (ただしr>g\geq0) \end{align*}
:期間 t :現在価値 P :1年後の配当額 D_1 :投資家の期待収益率 r :配当成長率 g
二段階成長配当割引モデル
- 配当額の成長率が、二段階に分かれて成長すると仮定したDDM。

\begin{align*} P &= \dfrac{D_1}{(1+r)} + \cdots + \dfrac{ (1+g_1)^{m-1}D_1 }{(1+r)^m} + \dfrac{ (1+g_2)^{m-1}D_m }{(1+r)^{m+1}} + \cdots+ \dfrac{(1+g_2)^{n-m}D_1}{(1+r)^n} \\\\ &= D_1\sum_{t=1}^{m}\dfrac{(1+g_1)^{t-1}}{(1+r)^t} + D_m\sum_{t=m+1}^{n}\dfrac{(1+g_2)^{t-m}}{(1+r)^t} \space \space \space \space \space \space \space \space (ただしr>g_2,\space g_2\geq0で,\space通常はg_1>g_2) \end{align*}
:期間 t :現在価値 P :m年後の配当額で D_m (1+g_1)^{m-1}D_1 :投資家の期待収益率 r :1~m年までの配当成長率 g_1 :m+1年以降の配当成長率 g_2
サスティナブル成長率 (Sustainable Growth Rate)
- 企業の利益成長率を表す指標
- 一定の仮定の下では、利益、自己資本、配当が全て同じ成長率。
ROEが一定、配当性向d
\begin{align*} 利益成長率 &= \dfrac{E_{t+1} - E_t}{E_t} \\\\ &= \dfrac{B_{t+1}ROE - E_t}{E_t} \\\\ &= \dfrac{\lbrace B_t+(1-d)E_t\rbrace ROE - E_t}{E_t} \\\\ &= \dfrac{(1-d)E_t ROE + B_t ROE - E_t}{E_t} \\\\ &= (1-d)ROE \end{align*}
: E_t 期の当期純利益 t
この仮定の下、以下の等式が成り立つ。
\begin{align*} 利益成長率 &= 自己資本成長率 \\\\ &= 配当成長率 \\\\ &= (1-配当性向)ROE \end{align*}
これをサスティナブル成長率という。
ポートフォリオ理論1
太田浩司の会計・ファイナンスホームページ「企業財務論」(14章)
リスクとリターン
- 自己の資産を投資する際に、様々なリスクを最小化し且つリターンを最大させることのできる組み合わせ、すなわち最適な資産分配を見つけ出す。
リターン
- 尺度:期待収益率(収益率の期待値)
\begin{align*} E[\~R] &= p_1R_1 + p_2R_2 + \cdots + p_nR_n \\\\ &= \sum_{i=1}^{n}p_iR_i \end{align*}
: p_i の生起確率 i \sum_{i=1}^{n}p_i = 1 : R_i の場合の収益率 i
リスク
- 尺度:標準偏差(収益率のばらつき)
\begin{align*} Var[\~R] &= E[\lbrace \~R_A - E(\~R_A)\rbrace^2 ] \\\\ &= \sum_{i=1}^{n}p_i \lbrace \~R_A - E(\~R_A)\rbrace^2 \\\\ &= p_1\lbrace \~R_1 - E(\~R)\rbrace^2 + p_2\lbrace \~R_2 - E(\~R)\rbrace^2 + \cdots + p_n\lbrace \~R_n - E(\~R)\rbrace^2 \\\\ &= \sigma^2 \end{align*}
\begin{align*} \sigma &= \sqrt{Var[\~R]} \\\\ &= \sqrt{\sum_{i=1}^{n}p_i\lbrace R_i - E(\~R)\rbrace^2} \end{align*}
-
Var[\~R] = \sigma^2 -
\sigma
2証券間の連動性
共分散
- 尺度:共分散
\begin{align*} Var[\~R] &= E[\lbrace \~R_A - E(\~R_A)\rbrace \lbrace \~R_B - E(\~R_B)\rbrace] \\\\ &= \sum_{i=1}^{n}p_i \lbrace \~R_A - E(\~R_A)\rbrace \lbrace \~R_B - E(\~R_B)\rbrace \\\\ &= p_1\lbrace \~R_{A1} - E(\~R_A)\rbrace \lbrace \~R_{B1} - E(\~R_B)\rbrace + p_2\lbrace \~R_{A2} - E(\~R_A)\rbrace \lbrace \~R_{B2} - E(\~R_B)\rbrace + \cdots +p_n\lbrace \~R_{An} - E(\~R_A)\rbrace \lbrace \~R_{Bn} - E(\~R_B)\rbrace \\\\ &= \sigma_{AB} \end{align*}
-
Var \lbrack \bar R \rbrack=\sigma^2 -
\sigma
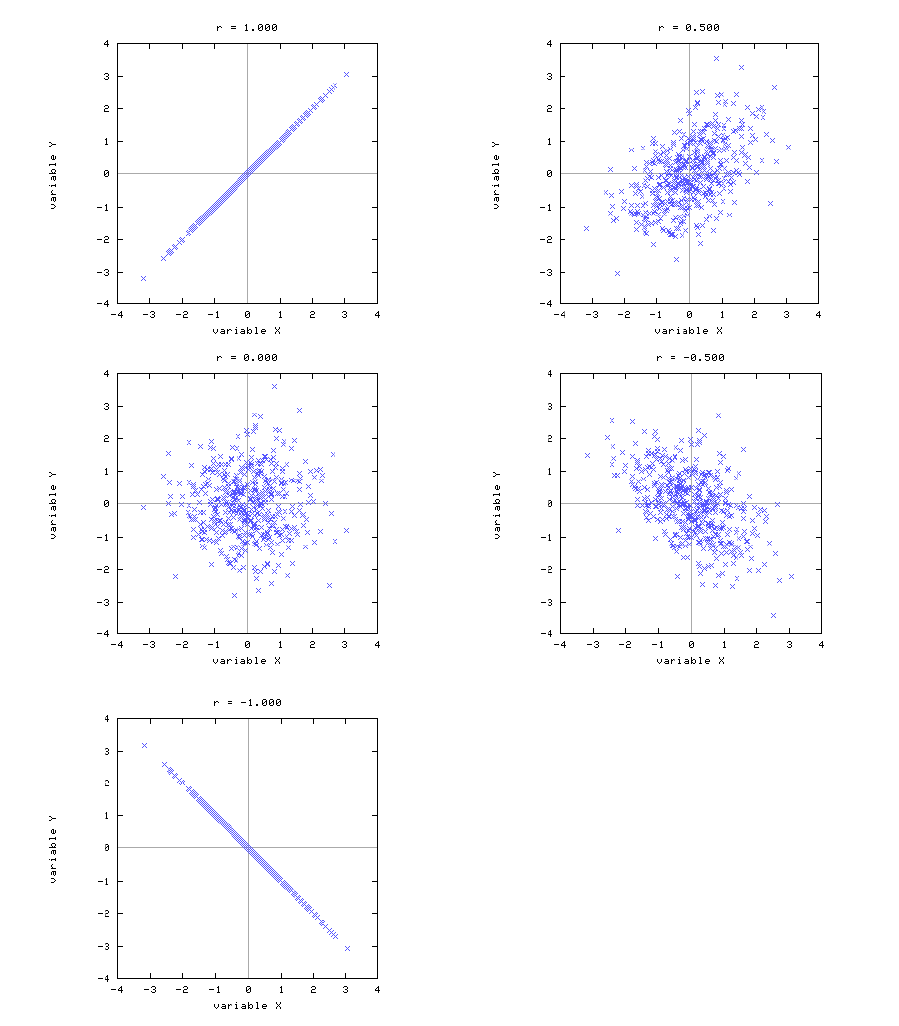
相関係数
- 2証券間の連動性を単位に影響を受けない指標
証券Aと証券Bの相関係数
\begin{align*} \rho_{AB} &= \dfrac{\rho_{AB}}{\rho_{A}\rho_{B}} \\\\ &= \cfrac{E[\lbrace\bar{R_A} - E(\bar{R_A}\rbrace \lbrace\bar{R_B} - E(\bar{R_B})\big\rbrace] }{ \sqrt{ E \big\lbrace\bar{R_A} - E(\bar{R_A}\rbrace^{2} } \sqrt{E \big\lbrace\bar{R_B} - E(\bar{R_B})\big\rbrace^{2} } } \end{align*}
- 相関係数(通常
\rho r -
-1 \leq \rho \leq 1 -
\rho<0 -
\rho=0 -
\rho>0