📈

多項式近似による活性化関数の計算量削減実験

2022/12/01に公開

機械学習

tech

TL;DR

高価な計算量を持つ活性化関数を微分可能なHardsigmoid付き多項式関数(1次項を括り出して残りの変数は区間でclampした関数)で近似する。

GELU: $G(x) = 0.5x(1+\text{tanh}(\sqrt{2/\pi}(x - 0.044x^3)))$
polyGELU: $f_G(x) = -0.0092x^4 + 0.2500x^2 + 0.5000x$

指数計算を含む高負荷な活性化関数を微分可能な形の多項式関数で近似することで、Swish形状の関数であれば本手法を用いて滑らかに近似可能で、計算量も小さくなる。

モチベーション

GELU[1]やSwish(SiLU)[2]、Mish[3]などの最近の活性化関数は指数計算(主にtanhやsigmoid)が入っており、エッジデバイス上など計算量がシビアな条件では採用を見送ることがある。例えばYOLOv7の実装[4]はGPU modelでSwishが使用されているが、より高速な条件をクリアするためのYOLOv7-tinyはLeakyReLUが使われている。また、MobileNetv3[5]ではSwishをHardswishとしてReLU6(HardSigmoidのmaxを6とした関数)を用いたクランプを挟んで2次関数を用いる近似で代用している。
しかし問題もあり、Hardswishはたったの2次でSwishを良く近似するが、グラフから分かるように $|x| = 3$ で微分不可能になっている。1次導関数のグラフはSwishを近似できているとは言えない。

Swish(黒)とHardswish(赤)

[2]によれば、非滑らかな関数であるReLUを用いたNNの出力は $x = 0$ の特異点に起因すると思われる鋭い領域があり、これに対しSwishを用いたNNの出力は滑らかなになっている。損失ランドスケープが滑らかであれば、NNの初期値および学習率に対する感度が低くなるため最適化が容易であると考えられる。この性質を考えると活性化関数が滑らかである方がよい。

[2]より、出力ランドスケープ
[3]より、ReLU, Mish, Swishの損失ランドスケープ

本稿では4次多項式をHardSigmoidでクランプすることで $x = 0$ 周辺で活性化関数を近似し、さらに端点でも導関数が連続である条件条件を課すことで、微分可能で、計算量も削減された活性化関数を作る。

4次多項式による近似の条件

Swish型の関数fは以下の性質をもつ。

$x \to -\infty$ で0に収束する
区間(-∞, 0]で $f(x) <= 0$
$f(0) = 0$
区間[0,∞)で単調増加する
$x \to +\infty$ で $f(x) = x$ に漸近する

実際Hardswishはこの条件を満たしていて、区間(-∞, -3]で0、[-3, 3]で2次関数 $f = x(x + 3)$ 、[3, +∞)で $x$ となっていて、実装は $H(x|a,b) = \text{max}(\text{min}(b,x),a)$ を用いて次の式で表せる。

\text{Hardswish}(x) = \frac{1}{6} x * H(x+3|0,6)

H(x+c|0,b)はクランプ用のHardsigmoidで、これの積により $d = b-c$ として区間[-c, d]だけ所望の多項式を適用することができるようになる。接続点は(-c, 0)と(d, d)。

さらに微分可能となるため次の条件を与える。

$f'(-c) = 0$
$f(-c) = 0$
$f'(d) = 1$
$f(d) = d$

この区間に4次関数を用いる。2次関数では変曲点が1つしかなく端点2つを滑らかに接合できない。3次関数では変曲点が2つのため、 $f(x) = 0$ 以外で $f(x) = x$ と滑らかに接続できないため、正の領域でSwishやMishを近似できない(GELUはこれらに比べ正域のカーブが小さいためある程度近似できる)。4次関数の負係数の凹曲線を用いてSwish型関数のの確率的正則化機能を近似し、微分可能な性質を保持しながら指数計算を排除した多項式で形状を再現する。

懸念点としては、[2]では微分が1であることはもはや現代のNNアーキテクタでは必須ではないことを示唆していること、[6]にあるように区間(-∞, -c]で勾配が常に0になるため学習が低速になる可能性があることが挙げられる。後者については負域で分数関数と接続するなどにより、活性化されていないときでも非ゼロな勾配を与えることができる。今回これらは考えず、計算量が小さいSwish型関数をつくることのみを目標とする。

関数の探索

条件を満たす4次関数として次の関数を用意する。

f(x) = \frac{ x * (x+c)^2 * (x-q) }{ (d+c)^2 * (d-q) }

cとqは探索するパラメータ。
$c > 0$
$q > 0$
端点dは $f'(x) = 1$ となる最大のx。解析的に求まる。
分母は $x > d$ において傾きを1にする正規化定数。

これをHardsigmoidによりクランプすると次になる。

f_{\text{poly}}(x) = \frac{ x * H(x+c| 0, d)^2 * (H(x+c| 0, d) -c -q) }{ (d+c)^2 * (d-q) }

区間[-c, d]では $f(x)$ に一致する。

近似する活性化関数と $f_{\text{poly}}(x)$ との誤差を最小化するようにcとqを変更していく。

実際にGELU, Swish, Mishに対してこれを適用すると、以下の関数が得られる。厳密に最適化したわけではなく、真の活性化関数と近似曲線のなす面積が最小になるように(c,q)が整数の範囲で試行した。

GELU:  c = 3, q = 6  (d = 3)
Swish: c = 4, q = 8  (d = 4)
Mish:  c = 4, q = 10 (d = 5.333...)

真の活性化関数

GELU: $G(x) = 0.5x(1+\text{tanh}(\sqrt{2}/\pi(x + 0.044715x^3)))$
Swish: $S(x) = x/(1 + e^{-x})$
Mish: $M(x) = x \text{tanh}(\text{log}(1 + e^{x}))$

近似した関数の曲線部分の式

GELU: $f_G(x) = -0.0092x^4 + 0.2500x^2 + 0.5000x$
Swish: $f_S(x) = -0.0039x^4 + 0.1875x^2 + 0.5000x$
Mish: $f_M(x) = -0.0024x^4 + 0.0049x^3 + 0.1574x^2 + 0.3936x$

4次の多項式で近似できており、GELUやSwishに関しては3次の項の係数が0になり2の累乗次の3項のみで表現できている。計算量が削減可能な形であり好ましい。

黒が真の活性化関数、赤が近似した4次関数、またその1次導関数

GELU
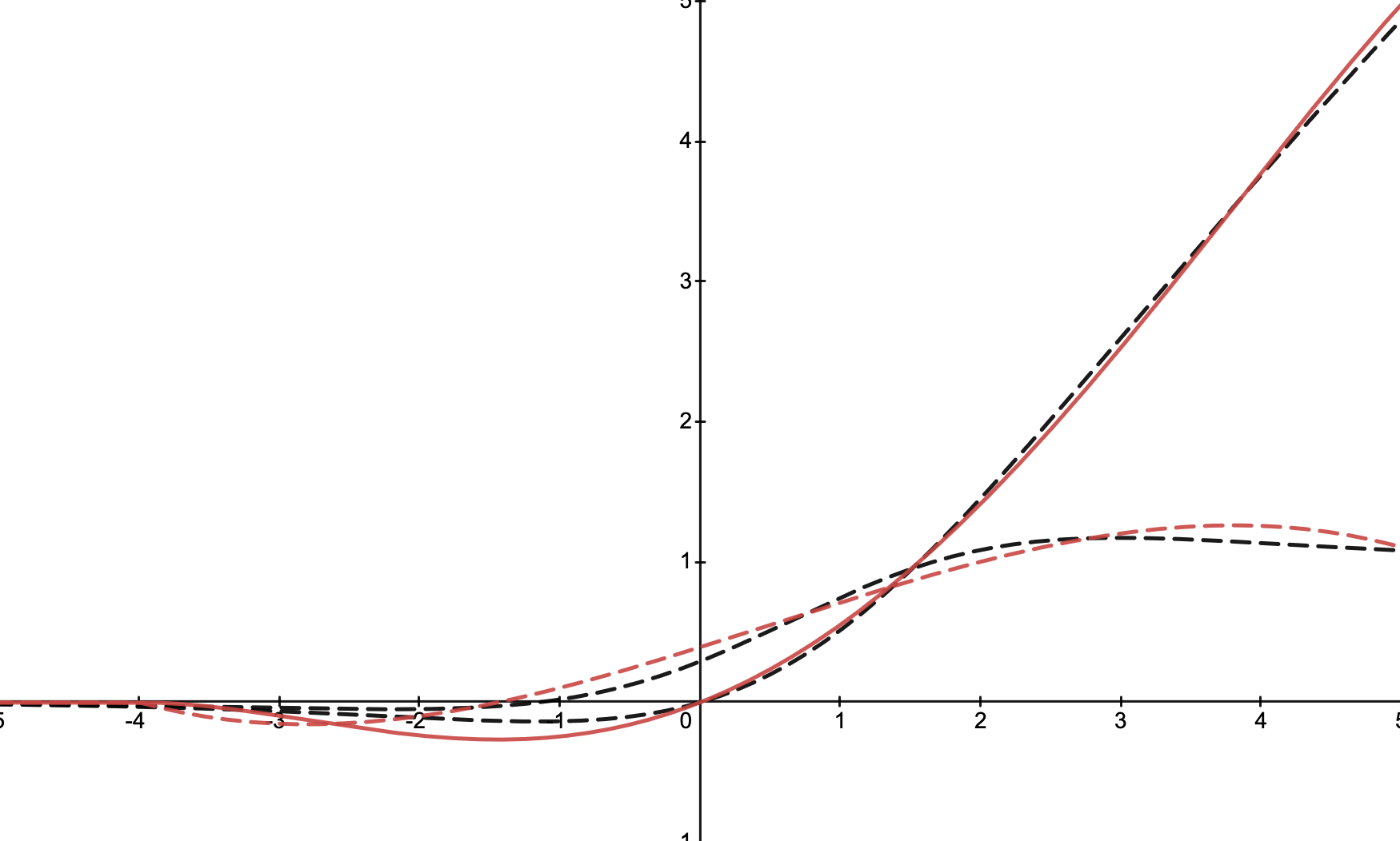Swish
Mish

数値実験

M2チップ上で各活性化関数を用いてtorch.tensorを処理したときの処理時間指標は以下となった。

ReLU:       521 
LeakyReLU:  526 
Tanh:       2588
Hardtanh:   528 
GELU:       5247
SiLU:       1749
Hardswish:  537 
Mish:       5655

これらはtorch._C._nnから呼ばれるC実装の関数が動くので単純に比較できないため、torch.nnのスクリプトで作成したMyHardswishを実装し、そのスケールでMishの近似Polymishと処理時間を比較する。

class Hardswish(nn.Module):
    def __init__(self):
        super().__init__()
        return None

    def forward(self, x):
        return F.hardswish(x)
        
        
class MyHardswish(nn.Module):
    def __init__(self):
        super().__init__()
        return None

    def forward(self, x):
        x_ = F.hardtanh(x+4.0, 0.0, 6.0)
        return x*x_/6
 
 
class Polymish(nn.Module):
    def __init__(self):
        super().__init__()
        return None

    def forward(self, x):
        x_ = F.hardtanh(x+4.0, 0.0, 9.33)
        return x*(x_**2)*(x_-14.0)/406.5

この処理時間指数は次のようになった。

Hardswish:   537
MyHardswish: 2524025
PolyMish:    4473932

積の回数が異なるので単純に比較できないが、torch._C._nnのスケールに直すと、処理時間指数5000のGELUやMishを処理時間指数1000程度の関数として処理できる可能性がある。Swishはもともと1700ほどの速度なのであまり高速化はできないかもしれない。

実際にCifar100を用いてconvnext_femtoの64epoch時点での精度を測定する。

ReLU:       0.334 
GELU:       0.361
Hardswish:  0.249 
Mish:       0.280
Polymish:   0.331

雑な設定で回したので比較はできないが学習はできている。

結論

微分可能な多項式活性化関数を作り、速度を参考程度に比較した。
実際の学習でも標準的な活性化関数をもちいた場合と同程度の精度が出るため、よい性能と両立した計算量の削減が期待できる。

追記: Pytorch2.0では徐々にC++実装がpythonに戻されるらしいので、より期待が高まっている。

参照

[1] Dan Hendrycks, Kevin Gimpel, "Gaussian Error Linear Units (GELUs)", 8 Jul 2020
[2] Prajit Ramachandran, Barret Zoph, Quoc V. Le, "Swish: a Self-Gated Activation Function", https://arxiv.org/abs/1710.05941v1, 16 Oct 2017
[3] Diganta Misra, "Mish: A Self Regularized Non-Monotonic Activation Function", https://arxiv.org/abs/1908.08681, BMVC 2020, 13 Aug 2020
[4] YOLOv7 config: https://github.com/WongKinYiu/yolov7/blob/eef4f2c92851e4d72c0630ee1f3615144353a73e/cfg/training/yolov7-tiny.yaml
[5] Andrew Howard, Mark Sandler, Grace Chu, Liang-Chieh Chen, Bo Chen, Mingxing Tan, Weijun Wang, Yukun Zhu, Ruoming Pang, Vijay Vasudevan, Quoc V. Le, Hartwig Adam, "Searching for MobileNetV3", https://arxiv.org/abs/1905.02244v5, ICCV 2019, 20 Nov 2019
[6] Maas, A.L., "Rectifier Nonlinearities Improve Neural Network Acoustic Models", ICML 2013

参考: Shiv Ram Dubey, Satish Kumar Singh, Bidyut Baran Chaudhuri, "Activation Functions in Deep Learning: A Comprehensive Survey and Benchmark", https://arxiv.org/abs/2109.14545 Neurocomputing, Elsevier, 28 Jun 2022
結局Swishっぽい形であれば精度が出たり出なかったりするらしい。

モチベーション

4次多項式による近似の条件

関数の探索

数値実験

結論

参照

Discussion