ランダムに並んでいるn個のデータに対してクイックソートを適用したときの,データ比較回数の平均値は,以下の漸化式を満たす.
- C_0 = C_1 = 0
- \displaystyle C_n = n+1 + \frac{2}{n} \sum^{n-1}_{k=0} C_k \quad (n>1)
本記事では,この漸化式を用いてクイックソートの平均時間計算量を求めていきます.
漸化式の解き方
方針
上記の漸化式には,
-
nによる割り算
-
nより小さいインデクスに関する和
の二つが含まれており,これらが漸化式を複雑にしています.そこで,これら二つを取り除くように式変形をしていきます.
nによる割り算の除去
まず,nによる割り算を除去するために両辺をn倍します.
\displaystyle nC_n = n^2+n + 2 \sum^{n-1}_{k=0} C_k \quad (n>1)
これで,nによる割り算を除去することができました.
nより小さいインデクスに関する和の除去
上式において,nをn-1に置き換えると,
\displaystyle (n-1)C_{n-1} = n^2-n + 2 \sum^{n-2}_{k=0} C_k \quad (n>2)
1番目の式から,2番目の式を引いて
nC_n - (n-1)C_{n-1} = 2n + 2 C_{n-1}
\therefore nC_n = (n+1)C_{n-1} + 2n \quad (n>2)
これで,和の計算を除去することができました.
漸化式を解く
上記操作により,漸化式がシンプルな形になったため実際に解いていきましょう.
まず両辺を(n+1)nで割ると,
\displaystyle \frac{C_n}{n+1} = \frac{C_{n-1}}{n} + \frac{2}{n+1} \quad (n>2)
となり,\displaystyle T_n = \frac{C_n}{n+1}とおくことで次式を得る.
\displaystyle T_n = T_{n-1} + \frac{2}{n+1} \quad (n>2)
この式を展開していくと,
\displaystyle T_n = T_{n-2} + \left(\frac{2}{n+1} + \frac{2}{n}\right)
\displaystyle T_n = T_{n-3} + \left(\frac{2}{n+1} + \frac{2}{n} + \frac{2}{n-1}\right)
のようになり,最終的にはn>2より以下の式にたどり着きます.
\displaystyle T_n = T_{2} + \left(\frac{2}{n+1} + \frac{2}{n} + \frac{2}{n-1} + \cdots + \frac{2}{3+1}\right)
ここで,
- \displaystyle T_2 = \frac{C_2}{2+1} = \frac{3}{3} = 1
- \displaystyle \frac{2}{n+1} + \frac{2}{n} + \frac{2}{n-1} + \cdots + \frac{2}{3+1} = 2\sum^{n}_{k=1}\frac{1}{k+1}-2\left(\frac{1}{2+1} + \frac{1}{1+1}\right) = 2\sum^{n}_{k=1}\frac{1}{k+1}-\frac{5}{3}
より,
\displaystyle T_n = 1+ \left(2\sum^{n}_{k=1}\frac{1}{k+1}-\frac{5}{3}\right)
\displaystyle \therefore T_n = 2\sum^{n}_{k=1}\frac{1}{k+1}-\frac{2}{3}.
最後に,\displaystyle T_n = \frac{C_n}{n+1}と置いたので,上式の両辺に(n+1)をかけて,
\displaystyle C_n = 2(n+1)\sum^{n}_{k=1}\frac{1}{k+1}-\frac{2}{3}(n+1).
以上より,n個のランダムなデータにクイックソートを適用したときの平均比較回数は
\displaystyle C_n = 2(n+1)\sum^{n}_{k=1}\frac{1}{k+1}-\frac{2}{3}(n+1).
調和級数
\displaystyle H_n = 1 + \frac{1}{2} + \frac{1}{3} + \cdots \frac{1}{n} = \sum^{n}_{k=1}\frac{1}{k}
は調和数(haemonic number)と呼ばれる.
調和数は,前節で求めたC_nにも\displaystyle \sum^{n}_{k=1}\frac{1}{k+1}という形で表れていることが分かる.
そこで,本節では調和数H_nを用いて,C_nを表してみる.
\displaystyle \sum^{n}_{k=1}\frac{1}{k+1} = \sum^{n+1}_{k=2}\frac{1}{k}
であるから,\displaystyle H_n = \sum^{n}_{k=1}\frac{1}{k}を用いるには,H_nから
という操作をすれば辻褄が合う.従って,
\displaystyle \sum^{n}_{k=1}\frac{1}{k+1} = \sum^{n}_{k=1}\frac{1}{k} - \frac{1}{1} + \frac{1}{n+1} = H_n - \frac{n}{n+1}.
以上より,
\displaystyle C_n = 2(n+1)\left(H_n - \frac{n}{n+1}\right) - \frac{2}{3}(n+1) = 2(n+1)H_n- \frac{8}{3}n-\frac{2}{3}
\displaystyle \therefore C_n = 2(n+1)H_n- \frac{8}{3}n-\frac{2}{3}.
調和級数の計算量の導出
T(n)がオーダーf(n)であるとき,その定義は
T(n) = O(f(n))
⇔ある実数c>0と自然数n_0が存在して,全てのn \geq n_0に対してT(n) \leq c \cdot f(n)が成り立つ
であり,f(n)はT(n)の漸近的上界(asymptotic upper bound)を意味する.
つまり,調和数の計算量を求めるには,H_n \leq c \cdot f(n)を満たすようなf(n)を探せば良い.
次の図において,黄色で示した長方形は\displaystyle H_n = \sum^{n}_{k=1} \frac{1}{k}の面積,青で示した部分は\displaystyle y=\frac{1}{x} \ (1 \leq x \leq n)とx軸に囲まれた部分の面積である.
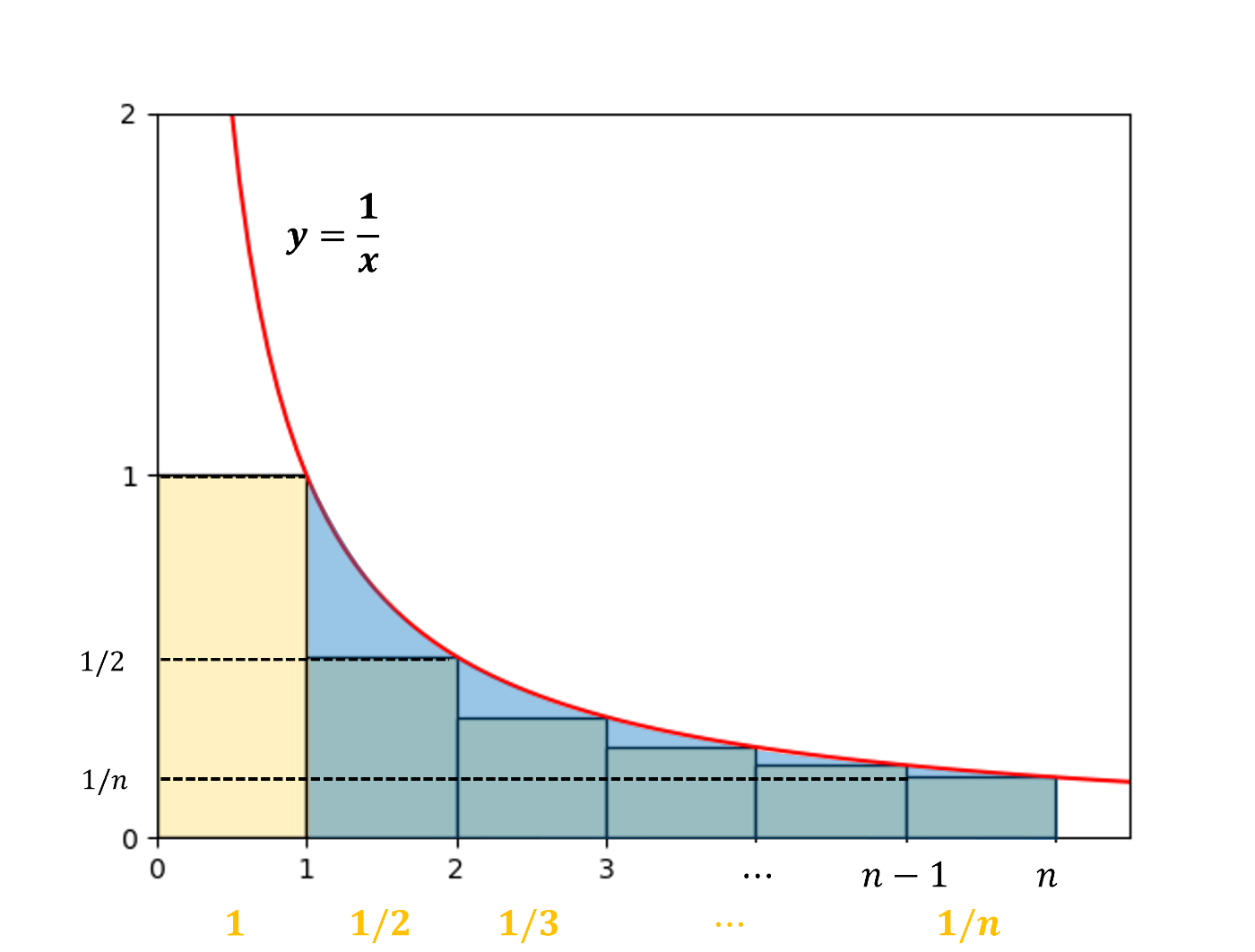
上図より,1 \leq x \leq nの範囲において,
「黄色の面積」\leq「青の面積」
であることは明らかである.
青で示した部分の面積は,積分を用いることで求めることができ,その値は
\displaystyle \int^{n}_{1} \frac{1}{x}dx
である.
従って以下の関係が成り立つ:
\displaystyle \sum^{n}_{k=2} \frac{1}{k} \leq \int^{n}_{1} \frac{1}{x}dx.
次に,図の左側に位置する面積1の長方形の面積を両辺に足すことで以下の関係を得る:
\displaystyle 1 + \sum^{n}_{k=2} \frac{1}{k} \leq 1+ \int^{n}_{1} \frac{1}{x}dx
\displaystyle \sum^{n}_{k=1} \frac{1}{k} \leq 1+ \int^{n}_{1} \frac{1}{x}dx \qquad \left(\because 1 + \sum^{n}_{k=2} \frac{1}{k} = \sum^{n}_{k=1} \frac{1}{k}\right)
\displaystyle \therefore H_n \leq 1+ \log n \qquad \left(\because \int^{n}_{1} \frac{1}{x}dx = \log n \right)
この関係は,全ての自然数nに対して成り立つため,ある実数c>0を用いて
H_n \leq c \cdot (1 + \log n).
以上より,H_n = O(\log n)であることが分かった.
クイックソートの平均時間計算量
さて,これまでの内容ではクイックソートの平均比較回数と調和数の計算量を求めてきました.それらの結果をまとめると,以下のようになります:
- \displaystyle C_n = 2(n+1)H_n- \frac{8}{3}n-\frac{2}{3}.
- H_n = O(\log n)
この二つの結果を用いてクイックソートの平均時間計算量を求めます.
まず,C_nの第一項目について,
2(n+1) = O(n),H_n = O(\log n)
なので,
2(n+1)H_n = O(n) O(\log n) = O(n \log n)
第二項目以降について,
\displaystyle -\frac{8}{3}n = O(n),\displaystyle -\frac{2}{3} = O(1)
なので,
\displaystyle -\frac{8}{3}n - \frac{2}{3}= O(n)O(1) = O(n)
上で求めた結果を合わせて,
C_n = O(n \log n) + O(n) = O(n\log n).
以上より,C_n = O(n\log n)となる.
参考文献

Discussion