Zenn
Closed26

Advent of Code 2023

adventofcode
ikdikd

Day 1: Trebuchet?!

https://adventofcode.com/2023/day/1

Part 1

英小文字と数字からなる文字列が与えられる。

文字列を前から見ていって現れる最初の数字と最後の数字をつなげて2桁の整数をつくる問題。

a1b2c3d4e5f → 15

解法

文字列を1文字ずつのリストに分解して、数字 1, 2, 3, 4, 5, 6, 7, 8, 9 のみを残す。リストの先頭と末尾を見て答える。

Part 2

「one」や「two」も数字と解釈して、最初の数字・最後の数字から2桁の整数をつくる。

xtwone3four -> 24

解法

Part 1 と異なり 1 文字がひとつの数字に対応するとは限らない。ただ、three, seven, eight を考慮しても、いま見ている文字の4文字先まで見て数字に変換していけばよい。

ikdikd

Day2: Cube Conundrum

https://adventofcode.com/2023/day/2

Part 1

バッグからキューブを取りだす予定

  • 赤キューブの個数
  • 緑キューブの個数
  • 青キューブの個数

が複数件与えられる。取りだしたキューブたちはそのつどバッグに戻す。

赤キューブ12個、緑キューブ13個、青キューブ14個あればすべての予定を達成できるか判定する問題。

解法

ひとつずつ予定を見て 赤 <= 12, 緑 <= 13, 青 <= 14 の条件を満たすか確かめればよい。

Part 2

すべての予定を達成するために必要な最小限の赤キューブ・緑キューブ・青キューブの個数を求める問題。

解法

赤・緑・青それぞれ独立に考えられる。たとえば、赤キューブの個数は「すべての予定にわたる赤キューブの個数最大値」にすればよい。

ikdikd

Day 3: Gear Ratios

https://adventofcode.com/2023/day/3

Part 1

二次元のグリッドが与えられる。

8 方位のいずれかで記号 (*, #, ...) に隣り合う数を列挙する問題。

次の例だと

  • 467 は 7 の右下に * があるため条件を満たす。
  • 114 は条件を満たさない。
467..114..
...*......
..35..633.
......#...
617*......
.....+.58.
..592.....
......755.
...$.*....
.664.598..

解法

それぞれの数について隣接 8 方向のマスを見る。記号は 1 マスだが数には「幅」があるので注意する。

Part 2

記号の中でも * は歯車だった。それぞれの歯車について隣り合う数を列挙する問題。

解法

Part 1 とだいたい同じ。

感想

数値のパースがちょっと厄介。

ikdikd

Day 4: Scratchcards

https://adventofcode.com/2023/day/4

Part 1

カードが与えられる。カードには、当たりの数リストと自分が持っている数のリストが書いてある。自分が持っている数のうち当たりであるものの個数を求める問題。

次の例だと、83, 86, 17, 48 の 4 個。

Card 1: 41 48 83 86 17 | 83 86  6 31 17  9 48 53

解法

自分が持っている数をひとつずつ見て条件を満たすか確かめればよい。

Part 2

カードが複数枚与えられる。カード 1 から順に使っていき、自分が持っていて当たりである数の個数 (= Part 1 の答え) だけ続くカードのコピーを受けとる。たとえば、カード 10 に条件を満たす数が 5 個あると、カード 11, 12, 13, 14, 15 のコピーを受けとる。最終的に (オリジナルとコピーの) カードを使う合計回数を求める問題。

解法

カード枚数の増え方は、(オリジナルのカード枚数に関して) 指数的なのでそのままシミュレーションすると実行が終わらない。

そこで、カード番号 \mapsto 現在の所持枚数　の連想配列を更新していけばよい。計算量はざっくり二乗で抑えられるはず。

ikdikd

Day 5: If You Give A Seed A Fertilizer

https://adventofcode.com/2023/day/5

Part 1

(ストーリーをよく分かってない)

seed の番号リストが与えられる。

seed の区間 → soil の区間　の平行移動による変換が複数与えられる。それぞれの変換は排反、つまり seed の区間たちは交差しない。

  • [50, 97] -> [52, 99]
  • [98, 99] -> [50, 51]

たとえば上の変換があるとき

  • seed 79 は soil 81 に移る
  • seed 98 は soil 50 に移る
  • seed 14 は soil 14 に移る

そして、seed → soil と同様に

  • soil → fertilizer
  • fertilizer → water
  • water → light
  • light → temperature
  • temperature → humidity
  • humidity → location

の変換も与えられる。最終的に seed が移った先の location 番号の最小値を求める問題。

解法

seed の個数 ≦ 20 のようなので、それぞれについて seed → soil → fertilizer → ... → location を辿っていけばよい。

Part 2

seed の番号リストだと思っていた入力

1778931867 1436999653 3684516104 2759374 1192793053 358764985 1698790056 76369598 3733854793 214008036 4054174000 171202266 3630057255 25954395 798587440 316327323 290129780 7039123 3334326492 246125391

を、ふたつずつペアにして

  • 1778931867, 1436999653
    • → seed が番号 1778931867 から 3215931519(=1778931867+1436999653-1) まである
  • ...
  • 3334326492, 246125391
    • → seed が番号 3334326492 から 3580451882(=3334326492+246125391-1) まである

と解釈する。

Part 1 と同じ変換をして行き着く先の location 番号の最小値を求める問題。

解法

Part 1 と異なり seed の個数が多いので番号をひとつずつ追っていくことはできない。

そこで、番号の区間リストを管理する。変換によって区間がたかだか 3 つの区間に分割される。最後に location の区間たちのそれぞれの左端を見て答えればよい。

seed → soil の変換は 30 個程度あり、soil 以降も同様なので最悪で区間が 90^7 個とかになり厳しい気がするが、実際は ≦ 200 に収まったのでOK (見積もり間違えてるかも？)

別解

seed の個数は ≦ 3e9 だったので、ひとつずつ Part 1 の要領で処理すると、速い言語では現実的な時間で終わる。

感想

Part 2 がかなり難しかったー。

ikdikd

Day 6: Wait For It

https://adventofcode.com/2023/day/6

Part 1

ボートレースの制限時間とこれまでの最高記録が与えられる。

レースは次の手順で進む。

  1. ボタンを好きな時間だけ押す
  2. ボタンを離す。k ミリ秒ボタンを押していたとき、速度が k mm/ms のボートが走る
  3. 制限時間までにボートの走った距離が記録になる

時間はボタンを押したタイミングから測られる。(ボタンを離してボートを走らせたタイミングではない)

最高記録を超えるボタンの押し方が何通りあるか求める問題。

解法

ボタンを押す時間を 1 ミリ秒、2 ミリ秒、…… と全通り試して、それぞれのレースでの記録を求めて最高記録を超えるか判定する。

与えられる制限時間を t ミリ秒として、ボタンを k ミリ秒押したとき、ボートの走る時間は t - k ミリ秒なので記録は k × (t - k) になる。

Part 2

Part 1 と同じだがレースの制限時間が長いケースが与えられる。

解法

入力が大きくなったが、それでもレースの制限時間 ≦ 10⁸ なので Part 1 と同じ解法で答えを求められる。

感想

Part 1 はもっとナイーブな解法があったのかも……？

ikdikd

Day 7: Camel Cards

https://adventofcode.com/2023/day/7

Part 1

ポーカーのようなゲーム。

カードが 13 種類：A, K, Q, J, T, 9, 8, ..., 2 あり、この順に強い。5 枚のカードからなる「手」のリストが与えられる。強い順に手を並び替える問題。

役は 7 種類：ファイブカード、フォーカード、フルハウス、スリーカード、ツーペア、ワンペア、ハイカード あり、この順に強い。手の強さはつくれる役の強さに従い、タイブレークは手を構成するカードの強さでおこなう。

解法

与えられた手でつくれる役を求めよう。種類別でカードを束にまとめたとき、それぞれの束が何枚のカードからなるかわかればよい。これはたとえば group by 的な処理でおこなえる。

役がわかれば手の並び替えは自然にできる。

Part 2

「J」のカードは実はジョーカーで、好きな種類のカードに置き換えて役をつくれる設定。

解法

「J」の枚数 0, 1, 2, 3, 4, 5 ごとにがんばって場合分けする。各ケースでは Part 1 と同じ要領で、つくれる役を求める。

ikdikd

Day 8: Haunted Wasteland

https://adventofcode.com/2023/day/8

Part 1

L/R からなる命令列とグラフが与えられる。グラフの各頂点から「L」「R」の有向辺が生えている。

頂点 AAA から命令列にしたがって頂点 ZZZ に至るまでの時間を求める問題。

命令列は LRR という形で与えられるが無限に続いているもの LRRLRRLRRLRR... と解釈する。

解法

頂点をひとつずつ移動していく。

Part 2

「A」で終わる頂点たちから一斉にスタートすることを考える。「Z」で終わる頂点に同時に着く時間を求める問題。

解法

実験してみると移動経路はこういう形になっていることがわかる。

さらに、A → Z までの時間と Z から一周して Z に戻ってくるまでの時間がたまたま等しい。

そこで連結成分ごとに Part 1 と同じタイプの時間を求めて LCM をとれば答えになる。

感想

Advent of Code によくある、入力によい特徴があることを期待して

  • 実験でたしかめる
  • 信じる

などを経て解く問題。

ikdikd

Day 9: Mirage Maintenance

https://adventofcode.com/2023/day/9

Part 1

整数列が与えられる。階差をとってあたらしい数列をつくる。数列のすべての要素が 0 になるまで続ける。手順をさかのぼって、各数列の末尾にひとつ要素を追加する。要素はパスカルの三角形の要領で決まる値にする。はじめに与えられた数列の末尾に追加される値を求める問題。

最初の数列が 1, 3, 6, 10, 15, 21 だと階差をとっていくと 0, 0, 0 になる。

1   3   6  10  15  21
  2   3   4   5   6
    1   1   1   1
      0   0   0

その後、各数列の末尾に追加する値は

  • 1 + 0 = 1
  • 6 + 1 = 7
  • 21 + 7 = 8

なので最終的にこうなる。

1   3   6  10  15  21  28
  2   3   4   5   6   7
    1   1   1   1   1
      0   0   0   0

解法

問題の入出力をそのまま関数にすると、自然に再帰的に実装できる。

Part 2

数列の末尾ではなく先頭に要素を追加する設定。ただし値は「和」ではなく「差」により決める。

最初の数列が 10, 13, 16, 21, 30, 45 の場合、いろいろあって最終的にこうなる。もとの数列の先頭に 5 が追加された。

5  10  13  16  21  30  45
  5   3   3   5   9  15
   -2   0   2   4   6
      2   2   2   2
        0   0   0

解法

Part 1 とだいたい同じ。

ikdikd

Day 10: Pipe Maze

https://adventofcode.com/2023/day/10

Part 1

線の描かれたタイルが敷き詰められていて、全体で線がひとつながりの閉路になっている。

閉路に含まれるタイルがひとつ指定される。閉路の上で最も遠いタイルまでの距離を求める問題。

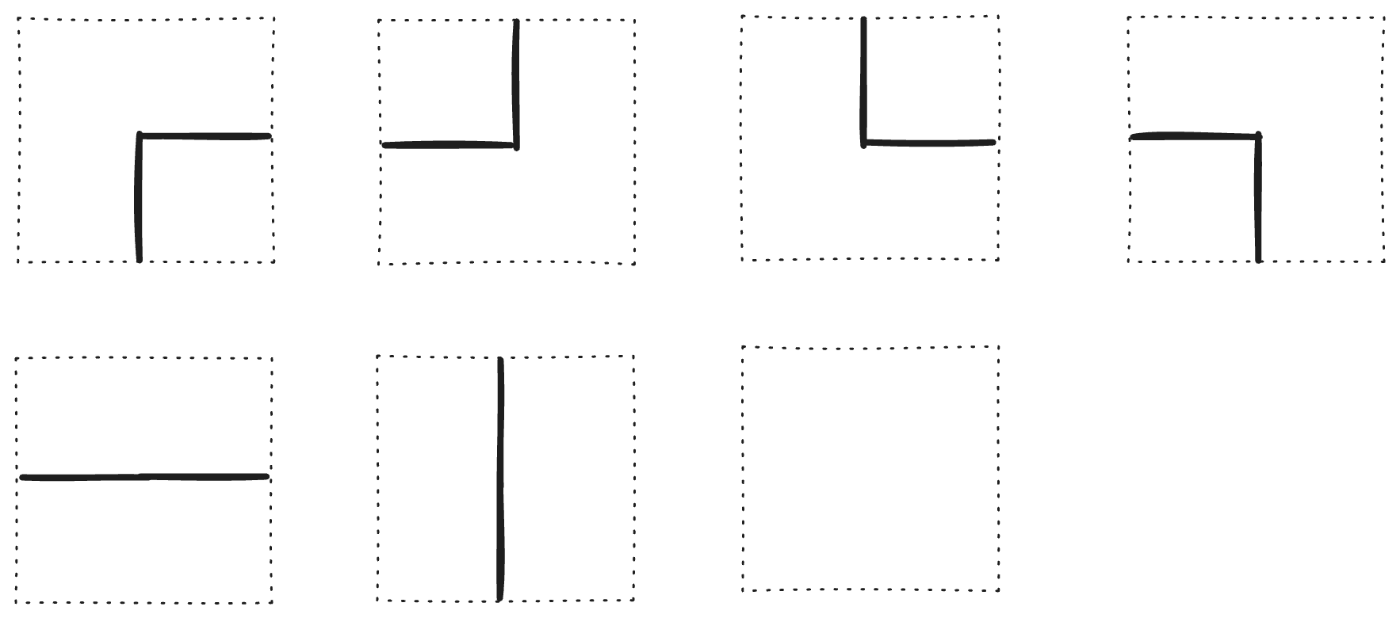
解法

スタートから閉路上を BFS して各タイルへの距離を求めればよい。

Part 2

閉路の内側にあるタイル数を求める問題。

こういう場合だと、中央の 8 個のタイルは閉路の外側であることに注意する。左下と右下は閉路の内側。

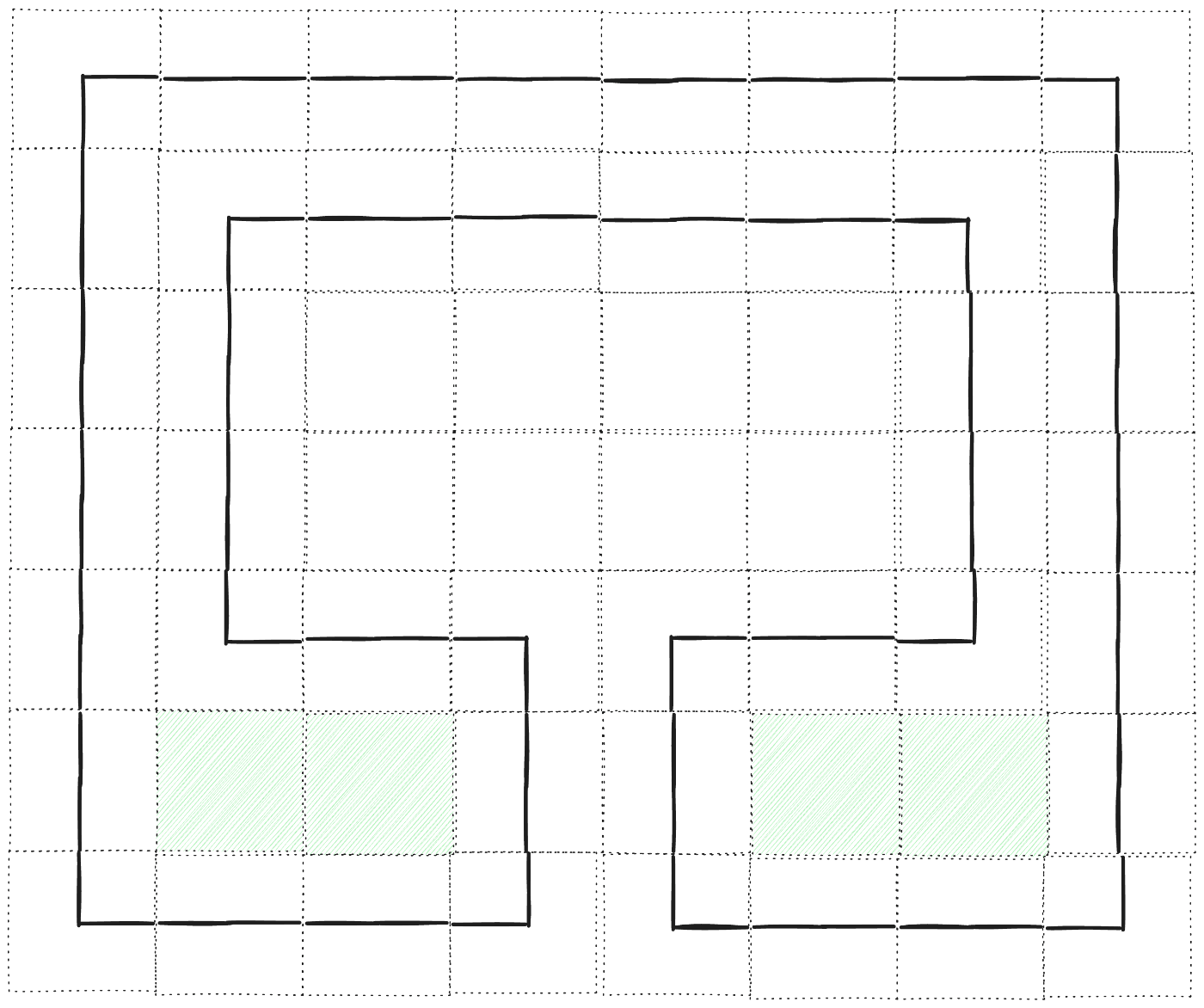
解法

DFS や BFS で外側のタイルを「塗る」解法 (★) だとうまくいかなそう。

そこで、各タイルが内側かどうかを even–odd rule により判定する。タイルから半直線を引いて閉路との交差回数が奇数なら内側、偶数なら外側。

別解

タイルを縦横「3倍」すると (★) で解ける。

ikdikd

Day 11: Cosmic Expansion

https://adventofcode.com/2023/day/11

Part 1

二次元グリッドが与えられる。. のみからなる行、列を 2 倍したグリッドを考える。# のペア全てにわたる距離の総和を求める問題。 距離は、隣り合う上下左右のマスへの移動回数で測る。

...#......
.......#..
#.........
..........
......#...
.#........
.........#
..........
.......#..
#...#.....

↓

....#........
.........#...
#............
.............
.............
........#....
.#...........
............#
.............
.............
.........#...
#....#.......

解法

問題文の通りにグリッドを「拡大」する。拡大後のグリッド上でふたつの # が

  • i_1 行目、j_1 列目
  • i_2 行目、j_2 列目

にあるとき、それらの距離はマンハッタン距離 ▲ |i_1 - i_2| + |j_1 - j_2| になる。

すべての # のペアについて ▲ の値の総和をとればよい。

Part 2

. のみからなる行、列を 1000000 倍したグリッドに対する問題。

解法

行と列をそれぞれ 1000000 増やすとグリッド全体では 1000000^2 増えるので、Part 1 と同様に素直にグリッドを拡大することはできない。

# のペアをひとつ固定して考えよう。もとのグリッドでの距離が d, 「2倍」グリッドでの距離が d + α とすると、「3倍」グリッドでは距離が d + 2α になる。より一般に「n倍」グリッドでは d + (n-1)α が言える。これは、マンハッタン距離を「行」の項と「列」の項に分けて考えると示せる。

「1倍」グリッド、「2倍」グリッド、…… における「行」の項が等差数列になることが分かり、「列」の項も等差数列になる。等差数列たちの和は等差数列になるので上に書いたことが従う。

結局、Part 1 に出てきた「2倍」グリッドでの # ペアの距離に加え、「1倍」グリッドでの距離を求めれば「n倍」グリッドでの距離も計算できる。あとはすべての # のペアについて総和をとる。

感想

けっこうシンプルに解ける問題でよかった。

ikdikd

Day 12: Hot Springs

https://adventofcode.com/2023/day/12

Part 1

., #, ? からなる文字列と整数列が与えられる。

すべての ? を . または # に置き換えてできる文字列は、? の個数を n として 2^n 個ある。その中で 「# の連続する長さ」の列が、与えられた整数列と等しいものの個数を求める問題。

  • ???.### / 1, 1, 3
    • #.#.### の 1 通り
  • .??..??...?##. / 1, 1, 3
    • 4 通りある
      • .#...#....###.
      • .#....#...###.
      • ..#..#....###.
      • ..#...#...###.

文字列の長さ ≦ 20

解法

? の個数が ≦ 20 と小さいので ? の置き換え方をすべて試せる。? 置換後の文字列が条件を満たすかは、たとえば run-length encoding を計算すればすぐにわかる。

Part 2

与えられた文字列と数列を 5 回繰り返してできる新しい文字列・数列に対して、Part 1 と同様に場合の数を求める問題。文字列の連結は間に ? を挟む。

???.### / 1, 1, 3 → ???.###????.###????.###????.###????.### / 1, 1, 3, 1, 1, 3, 1, 1, 3, 1, 1, 3, 1, 1, 3

解法

文字列の長さが最大で 100 近くになる。Part 1 の解法だと指数時間かかるので別の方法を考える。

たとえば dp[i][j] を、文字列の先頭 i 文字目まで、数列の先頭 j 項目までを考慮したときの場合の数、とすれば (i, j) の昇順に決まる。

与えられる文字列を S, 数列を A としよう。最終的な答えは dp[len(S)][len(A)] になる。

S[i] の文字で場合分けをする。

  • . のとき
    • 数列を「消費」しないので j は変えず \mathrm{dp}[i][j] \overset{+}{\to} \mathrm{dp}[i + 1][j] と更新する
  • # のとき
    • 位置 i から始まる # の連続する長さを A[j] と等しくすることを考える
      • S[i], S[i + 1], ..., S[i + A[j] - 1] がすべて # or ?
        • ? → # に置き換えれば # をつなげられる
      • S[i + A[j]] が . or ?
        • ? → . に置き換えれば # の連続を切れる
    • 上の条件ふたつ両方を満たしているときに \mathrm{dp}[i][j] \overset{+}{\to} \mathrm{dp}[i + \mathrm{A}[j] + 1][j + 1] と更新する
  • ? のとき
    • 上の「. のとき」「# のとき」と同じ式で dp テーブルを更新する

感想

DP の式が若干ややこしい。

添字をキーに持つのではなくて (部分) 文字列を直接扱うとすこし簡単になるかも。

ikdikd

Day 13: Point of Incidence

https://adventofcode.com/2023/day/13

Part 1

., # からなるグリッドが与えられる。鏡映しになっている位置を求める問題。

例1

#.##..##.
..#.##.#.
##......#
##......#
..#.##.#.
..##..##.
#.#.##.#.

↓

5列目と6列目の間

123456789
    ><   
#.##..##.
..#.##.#.
##......#
##......#
..#.##.#.
..##..##.
#.#.##.#.
    ><   
123456789

例2

#...##..#
#....#..#
..##..###
#####.##.
#####.##.
..##..###
#....#..#

↓

4行目と5行目の間

1 #...##..# 1
2 #....#..# 2
3 ..##..### 3
4v#####.##.v4
5^#####.##.^5
6 ..##..### 6
7 #....#..# 7

解法

  • 1列目と2列目の間、2列目と3列目の間、……
  • 1行目と2行目の間、2行目と3行目の間、……

をぜんぶ試して条件を満たすかチェックする。

Part 2

一箇所だけ . → # or # → . に変える。変更後に鏡映しになっている位置を求める問題。

解法

., # を反転させるマスをぜんぶ試す。あとは Part 1 と同じ。

グリッドの高さ、幅は ≦ 15 と小さい。

ikdikd

Day 14: Parabolic Reflector Dish

https://adventofcode.com/2023/day/14

Part 1

., #, O からなるグリッドが与えられる。グリッドを「傾ける」と丸い岩 O は傾けた方向に寄る。四角の岩 # は動かない。

グリッドを北に傾けたあとの丸い岩の位置を求める問題。

O....#....
O.OO#....#
.....##...
OO.#O....O
.O.....O#.
O.#..O.#.#
..O..#O..O
.......O..
#....###..
#OO..#....

↓

OOOO.#.O..
OO..#....#
OO..O##..O
O..#.OO...
........#.
..#....#.#
..O..#.O.O
..O.......
#....###..
#....#....

解法

一次元のリストで岩を傾ける処理を実装する。グリッドの transpose と組み合わせると欲しい操作ができる。

Part 2

「グリッドを 北、西、南、東 に傾ける」を 1 ステップとして、1000000000 ステップ繰り返したあとの丸い岩の位置を求める問題。

解法

グリッドの高さ、幅 = 100 で、グリッドを「傾ける」操作はおよそ 2 乗の計算量なので、1000000000 ステップを素直に実行するのはきびしい。

実験するとグリッドの状態 (丸い岩の位置) に周期性がありそう。

そこでグリッドの状態をキーに、ステップ数を値に持つ連想配列を管理して、「ループ」を飛ばすと高速化できる。

感想

周期性を使う Advent of Code あるある。

ikdikd

Day 15: Lens Library

https://adventofcode.com/2023/day/15

Part 1

文字列が与えられる。ASCII コードの列とみなして、掛け算や剰余をとってハッシュ値を求める問題。

'HASH' の場合

((((ord('H') * 17 % 256)
    + ord('A')) * 17 % 256
    + ord('S')) * 17 % 256
    + ord('H')) * 17 % 256

→ 52

解法

問題文の通りに計算する。

Part 2

hash map で連想配列を自作する問題。

カンマ , 区切りでこういう命令列が与えられる：rn=1,cm-,qp=3,cm=2,qp-,pc=4,ot=9,ab=5,pc-,pc=6,ot=7

  • 「rn=1」はキー hash('rn') の位置に ('rn', 1) を追加
    • すでに ('rn', *) があれば数値を更新
  • 「cm-」はキー hash('cm') に対応する値から ('cm', *) を削除
    • ('cm', *) がなければ何もしない

を意味する。ハッシュ関数は Part 1 で実装したもの。

連想配列の値は (string, int) のリスト。たとえば rn=1,cm=2 を実行したあとの連想配列は {0: [('rn', 1), ('cm', 2)]} になる。hash('rn') = hash('cm') = 0 に注意する。

解法

計算量はとくに気にしなくてよさそうなので素直に実装する。

ハッシュ値は 0 〜 255 の整数になるのでデータは配列で管理できる。

ikdikd

Day 16: The Floor Will Be Lava

https://adventofcode.com/2023/day/16

Part 1

., |, -, /, \ からなるグリッドが与えられる。|, -, /, \ は「鏡」で光を反射する。

  • |：左 (or 右) から光が来ると上下両方に光を放つ。上から来た光は下に、下から来た光は上に素通りさせる
  • -：「|」の反対
  • /：左から来た光を上に、上から来た光を左に、右から来た光を下に、下から来た光を右に導く
  • \：「/」の反対

一番左上のマスから右向きに光を発射する。光が通るマスの個数を求める問題。

.|...\....
|.-.\.....
.....|-...
........|.
..........
.........\
..../.\\..
.-.-/..|..
.|....-|.\
..//.|....

↓

######....
.#...#....
.#...#####
.#...##...
.#...##...
.#...##...
.#..####..
########..
.#######..
.#...#.#..

解法

光の経路をひとつずつ進めることを考える。

反射のルールからわかるように、「次のマス」を決めるには現在の位置だけでなく光が進む向きの情報も必要。

頂点を (行, 列, 方向) としたグラフ上で DFS や BFS をして解ける。

Part 2

グリッドの縁の好きなマスから光を発射できる。最初の向きも自由に決められる。光が通るマスの個数の最大値を求める問題。

解法

スタートの位置と向きの組み合わせはたかだか 100 × 100 × 4 通り。それぞれについて Part 1 と同様の計算をして最大値をとる。

ikdikd

Day 17: Clumsy Crucible

https://adventofcode.com/2023/day/17

Part 1

各マスに正整数が書かれたグリッドが与えられる。グリッドの左上から右下まで移動する最小コストを求める問題。コストは、通ったマスに書かれた数の総和で定める。

同じ向きへの移動は最大で3回連続まで。たとえば3回連続で右に動いたら次は右以外に移らないといけない。

解法

頂点を (行, 列, 方向) としたグラフ上で dijkstra

頂点 (i, j, 右) からは

  • (i - 1, j, 上)
  • (i - 2, j, 上)
  • (i - 3, j, 上)
  • (i + 1, j, 下)
  • (i + 2, j, 下)
  • (i + 3, j, 下)

に辺を引く。「左」は不要なはず。(i, j, 左), (i, j, 上), (i, j, 下) も同じように辺を引く。

辺の数は頂点数の 10 倍くらいで抑えられるので十分小さい。

Part 2

同じ向きへの移動が 4 回以上 10 回未満の制限になった問題。

解法

Part 1 とほとんど同じ。

感想

dijkstra でなくても bellman-ford とかでよいかも。

「この向きに移動した回数」を頂点に持たせる実装もありそう。

ikdikd

Day 18: Lavaduct Lagoon

https://adventofcode.com/2023/day/18

Part 1

グリッド上の閉路を表す (向き, 移動量) のリストが与えられる。閉路の周を含む内部のマスの個数を求める問題。

  • 移動量 ≦ 15
  • 移動回数 = リストの長さ ≦ 700

右に6、下に5、左に2、……と進む例

R 6
D 5
L 2
︙

解法

マス (i, j) が閉路に含まれるかの情報を二次元配列で持てる。(★)

あとは、たとえば閉路を囲む bounding box を考えて閉路の「外部」の面積を求めよう。bounding box の面積から閉路外部の面積を引けば答えになる。

確実に外部であることがわかる、bounding box 左上隅のマスから始めて、(★) を見て DFS や BFS をすれば外部のマスを列挙できる。

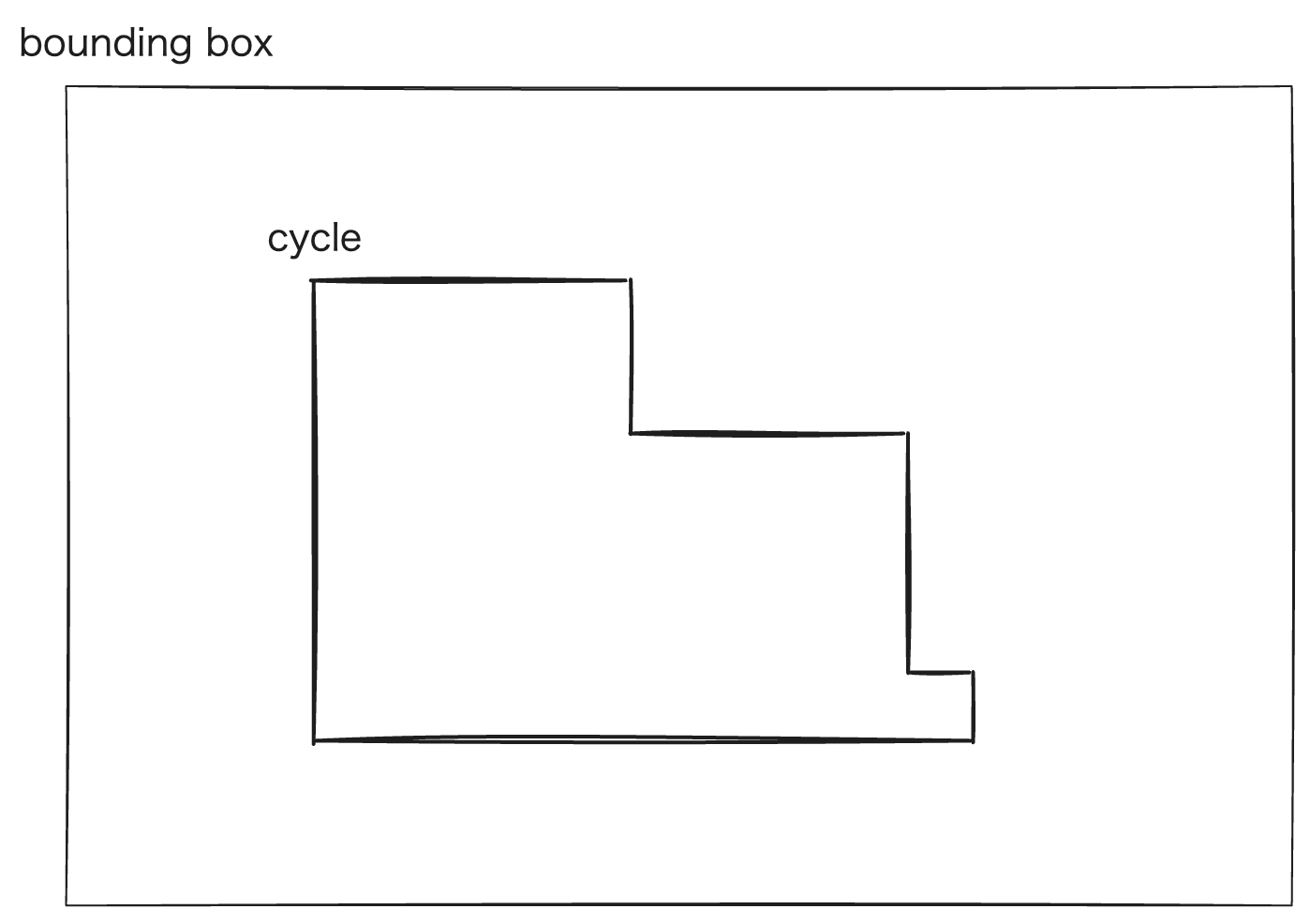
(直接、閉路内部の面積を求められる気もする。あるマスが内部かどうかは even–odd rule でわかる。)

Part 2

(向き, 移動量) の移動量が最大 400000 ほどになった問題。

解法

閉路の面積がざっくり 400000^2 以上になりうるので Part 1 (★) の方法はそのままではメモリに乗らない。

いわゆる座標圧縮で解く。

閉路の「角」の x 座標は (移動量によらず) 700 種類で抑えられることを利用する。y 座標も同じ。

x 座標と「順位」の対応付け、つまり

  • 1, 4, 10, 17, 19, 23
  • → 0, 1, 2, 3, 4, 5

こういう変換を考えると、0 ≦ x ≦ 700, 0 ≦ y ≦ 700 の範囲の問題になる。Part 1 (★) と同じ方法でほぼ解ける。

面積を求めるためには移動量の情報を復元する必要がある。たとえば順位「2」と「5」の元の座標における距離は、10 と 23 の距離、というふうにわかる。x 座標と y 座標の両方で考えると少しややこしいが面積を求められる。

別解

shoelace formula を使うときれいに解けそう。

感想

2次元の座標圧縮 混乱する〜

グリッドのマスが幅を持っているので厄介な気がする。

ikdikd

Day 19: Aplenty

https://adventofcode.com/2023/day/19

Part 1

4つの数値 x, m, a, s が与えられる。これは部品の4カテゴリにおける評価を表す。

頂点が

  • 「accept」頂点
  • 「reject」頂点
  • 中間頂点

の3種類ある。中間頂点では次のような規則で部品を次の頂点に送る。指定された頂点から始めて、最終的に部品が accept か reject のどちらにたどり着くか求める問題。

if a < 2006:
    goto ●
elif m > 2090:
    goto ▲
else:
    goto ■

解法

入力のパースが少し厄介だけど問題に書いてある通りに実装する。

Part 2

部品がひとつではなくたくさんある状況を考える。

具体的には、x, m, a, s がそれぞれ 1 以上 4000 以下の整数を動く。これら 4000^4 個の部品のうち accept 頂点にたどり着く個数を求める問題。

解法

取りうる x の値の集合 ⊆ {1, 2, ..., 4000}, m の集合, a の集合, s の集合を管理する。

中間頂点を通るたびに、「if」のどの条件を満たすかに応じて取りうる値の集合が狭まる。

if a < 2006:
    # x ∈ {1, 2, ..., 4000}
    # m ∈ {1, 2, ..., 4000}
    # a ∈ {1, 2, ..., 2005}
    # s ∈ {1, 2, ..., 4000}
    goto ●
elif m > 2090:
    # x ∈ {1, 2, ..., 4000}
    # m ∈ {2091, 2092, ..., 4000}
    # a ∈ {2006, 2007, ..., 4000}
    # s ∈ {1, 2, ..., 4000}
    goto ▲
else:
    # x ∈ {1, 2, ..., 4000}
    # m ∈ {1, 2, ..., 2089}
    # a ∈ {2006, 2007, ..., 4000}
    # s ∈ {1, 2, ..., 4000}
    goto ■

スタートの頂点から DFS や BFS をして、各頂点における「(x の集合, m の集合, a の集合, s の集合) のリスト」を更新していけばよい。リストの要素が、部品の通った経路に対応する。

最後に accept 頂点を見ると (x, m, a, s) の組合わせの個数が分かる。(x の集合) × (m の集合) × (a の集合) × (s の集合)

感想

Part 2 がむずかしい。解法の説明もむずかしい。

ikdikd

Day 20: Pulse Propagation

https://adventofcode.com/2023/day/20

Part 1

順序回路が題材？

ボタンを押すと「broadcaster」につながっている素子ぜんぶに low パルスが送られる。パルスは low と high の 2 種類がある。

素子は 3 種類ある。

  • flip-flop
    • on/off の状態をもつ
    • 入力されたパルスの low/high と状態 on/off から、次の状態と出力するパルスを計算、宛先の素子たちへパルスを送る
  • conjunction
    • 入力素子たちが前回送ってきたパルスの high/low を記憶している
    • 入力されたパルスをもとにメモリを更新して、出力するパルスを計算、宛先の素子たちへパルスを送る
  • untyped
    • パルスを受けとるだけ

1000 回ボタンを押したときに、素子が送った low パルスの回数・high パルスの回数の合計を求める問題。

解法

若干ややこしいけど問題文の通りに実装する。

1 回ボタンを押すたびに、それぞれの flip-flop, conjunction 内部が変わりうることに注意する。

Part 2

「rx」という名前のついた素子に low パルスがちょうど一回送られる、が起こるのはボタンを何回押したあとか求める問題。

解法

与えられた入力を観察すると、素子同士の接続はこうなっていて、A, B, C, D の出力の挙動を調べればよいと分かる。

実験すると A, B, C, D の出力はそれぞれ短め (≦ 5000) の周期を持つ。これらの LCM を考えると答えが出る。

感想

むずい。

ikdikd

Day 21: Step Counter

https://adventofcode.com/2023/day/21

Part 1

., # からなるグリッドが与えられる。# は壁でそのマスには移動できない。

はじめ一箇所に石が置かれている。1ステップで石は隣接する4方向に分裂する。64ステップ後に石があるマスの個数を求める問題。

壁がまったくない場合で、石の移動を2ステップ目まで描いた図。

.....
.....
..O..
.....
.....

.....
..O..
.O.O.
..O..
.....

..O..
.O.O.
O.O.O
.O.O.
..O..

解法

そのまま実装する。

Part 2

グリッドが上下左右繰り返されて無限に広い設定。26501365ステップ後に石があるマスの個数を求める問題。

解法

1ステップの処理に石の個数オーダーの計算量かかるので、なにかしら工夫する必要がある。

Part 1 で 64 ステップ終了後の石の配置を眺める。運よく、ひし型の縁に壁 # がないことがわかる。

Part1の図

ざっくり 64 + 64 × 2 ステップ終了後には再びこの形が表われると予想できる。

すこし補正すると 26501365 = 65 + (65 × 2 + 1) × 202300 ときれいに書ける。

相似的な形が拡大(?)していくので

  • 65 ステップ後の石の個数
  • 65 + (65 × 2 + 1) ステップ終了後の石の個数
  • 65 + (65 × 2 + 1) × 2 ステップ終了後の石の個数
  • 65 + (65 × 2 + 1) × 3 ステップ終了後の石の個数
  • ︙

に規則性がありそう。階差をとった列が等差数列だとエスパーして、欲しい答え 65 + (65 × 2 + 1) × 202300 ステップ終了後の石の個数 を求められる。

ikdikd

Day 22: Sand Slabs

https://adventofcode.com/2023/day/22

Part 1

ジェンガ。ピースは 1 × 1 × n の直方体。

宙に浮いているピースたちが与えられる。自由落下させると各ピースは底につくか他のピースに引っかかって止まる。

各ピースについて、安全に抜けるか、つまり、そのピースを抜いても上のピースたちが止まったままかを求める問題。

解法

「ピースたちの位置を入力、自由落下後のピースたちの位置を出力」とする関数を実装する。これで安全でないピースがわかり、余事象を考えて答えを求められる。

Part 2

安全でないピースを抜いたとき、落ちてくるピースと止まったままのピースがある。落ちてくるピースの個数を求める問題。

解法

Part 1 で実装した処理を流用して答えられる。

感想

けっこう素直な問題？

ikdikd

Day 23: A Long Walk

https://adventofcode.com/2023/day/23

Part 1

., #, <, ^, >, v からなるグリッドが与えられる。

# は壁で通れない。<, ^, >, v のマスでは、左、上、右、下にのみ動ける。

スタート (左上) からゴール (右下) まで同じマスを通らない経路の最長距離を求める問題。

#.#####################
#.......#########...###
#######.#########.#.###
###.....#.>.>.###.#.###
###v#####.#v#.###.#.###
###.>...#.#.#.....#...#
###v###.#.#.#########.#
###...#.#.#.......#...#
#####.#.#.#######.#.###
#.....#.#.#.......#...#
#.#####.#.#.#########v#
#.#...#...#...###...>.#
#.#.#v#######v###.###v#
#...#.>.#...>.>.#.###.#
#####v#.#.###v#.#.###.#
#.....#...#...#.#.#...#
#.#########.###.#.#.###
#...###...#...#...#.###
###.###.#.###v#####v###
#...#...#.#.>.>.#.>.###
#.###.###.#.###.#.#v###
#.....###...###...#...#
#####################.#

解法

入力を観察すると、<, ^, >, v によってグラフが DAG になってそう。

したがって dp(i, j) := スタートからマス (i, j) までの最長距離 をメモ化再帰で実装すると解ける。

Part 2

<, ^, >, v を . とみなして、最長距離を求める問題。

解法

再び入力を観察する。ほとんどが一本道であり、@ で示したような「交差点」は少ないことがわかる。

交差点を頂点、一本道でつながった交差点の間に辺を張ったグラフを考える。辺の重みは交差点の間の最長距離、これは経路が一通りなので簡単に求められる。

上で作ったグラフは頂点数が少ない (≦ 36) ので、通った頂点をぜんぶ覚えておく DFS (BFS?) で答えを出せる。

#.#####################
#.......#########...###
#######.#########.#.###
###.....#.>@>.###.#.###
###v#####.#v#.###.#.###
###@>...#.#.#.....#...#
###v###.#.#.#########.#
###...#.#.#.......#...#
#####.#.#.#######.#.###

感想

よかった。

ikdikd

Day 24: Never Tell Me The Odds

https://adventofcode.com/2023/day/24

Part 1

3次元空間にある石たちの座標・速度が与えられる。

z 軸は無視して、xy 平面の特定の矩形内で、軌跡が交差するような石のペアの個数を求める問題。

解法

ふたつの石の座標を (x_1, y_1, z_1), (x_2, y_2, z_2), 速度を (v_{x, 1}, v_{y, 1}, v_{z, 1}), (v_{x, 2}, v_{y, 2}, v_{z, 2}) として、連立方程式

  • x_1 + s v_{x, 1} = x_2 + t v_{x, 2}
  • y_1 + s v_{y, 1} = y_2 + t v_{y, 2}
  • s \geq 0, t \geq 0

を解くと、軌跡の交差する座標 P、一つ目の石が P に着くまでの時間、二つ目の石が P に着くまでの時間がわかり、答えを求められる。

連立方程式は中学数学を思いだして、式変形をして s を消して t のみの方程式にして解いた。Python とかだとライブラリを使うのもあり。

Part 2

好きな整数の座標に置いた岩を、好きな整数の速度で放つことができる。この岩にすべての石が同時に一箇所で衝突する座標を求める問題。

解法

速度が整数であることを活かそう。岩の x 方向の速度 v_x, y 方向の速度 v_y, z 方向の速度 v_z を適当な範囲ぜんぶ試す。

岩の速度に対するそれぞれの石の相対速度を考えると、すべての石が衝突する点があれば、そこが岩の座標となる。たぶん。

適当に石を 3 つ取り、石A, 石B, 石C とする。石Aと石Bが (岩に対する相対速度のもとで) 衝突する (x, y, z)、石Aと石Cが衝突する (x, y, z) が一致しないといけない。この (x, y, z) が固定した v_x, v_y, v_z における岩の座標の候補となる。

あとは、A, B, C 以外のすべての石について岩との衝突を見れば、上で出した (x, y, z) が岩の座標として妥当か確かめられる。

3 次元での衝突には xy 平面での衝突が必要なので、いい感じに Part 1 の処理を流用できる。

浮動小数点数だと精度が問題になりそうなので有理数などを使わないといけないかも。

ikdikd

Day 25: Snowverload

https://adventofcode.com/2023/day/25

Part 1

単純無向連結グラフが与えられる。

辺を 3 本削除してふたつの連結成分に分けられることが保証されている。それぞれの連結成分を求める問題。

頂点数 ≒ 1500

解法

辺の削除の仕方は一意っぽい？

適当な頂点をひとつ取って A とする。どのように辺を 3 本削除しても A と連結のままになる頂点の条件を考える。A から 4 通り以上の (辺素な) ルートで到達できる頂点たち、それ以外の頂点たち、と分ければよさそう。

計算量は頂点数の 3 乗か 4 乗くらいになる。(?)

別解

最小カットの問題とみて、乱択アルゴリズムのひとつである Karger's algorithm https://en.wikipedia.org/wiki/Karger's_algorithm を使えるらしい。

Part 2

なし

このスクラップは3ヶ月前にクローズされました