競プロメモ

ikd

??? 〜 2021年: https://scrapbox.io/ia7ck-comp-pro

ikd

ARC 147 A - Max Mod Min

操作回数がそこまで大きくならないことから、操作をシミュレーションすることで解ける。

実際、 $A_i := \max A$ は 1 回の操作で半分以下になる。 $A_j := \min A$ とおく。 $A_i$ を $A_j$ で割った余り $A_i \mod A_j$ が $A_i / 2$ 以下になることを示そう。

余りは割る数未満 $A_i \mod A_j < A_j$ なので $A_j \le A_i / 2 \Rightarrow A_i \mod A_j < A_i / 2$
$A_j > A_i / 2 \Rightarrow A_i - A_j < A_i / 2$ より $A_i \mod A_j = (A_i - A_j) \mod A_j < A_i / 2$

よって $A_i$ は 1 回の操作で半分以下になるため、合計操作回数は $O(\sum \log A_i) = O(N \log \max A_i)$

ikd

ABC 269 F - Numbered Checker

ていねいに等差数列の和を計算する問題。

クエリで与えられた二次元領域の左上 (マス $(A, C)$ ) に $x \ne 0$ が書かれているとする。 $x = 0$ の場合、つまり $A + C$ が奇数の場合もほとんど同じ。

整数は以下のように並んでいる。 $A$ 行目、 $A + 2$ 行目、 $A + 4$ 行目、……の答えへの寄与の合計を求めよう。 $A + 1$ 行目、 $A + 3$ 行目、……の寄与も同様に求められる。

   x  0    x+2  0     x+4  0  ...
   0  *      0  *       0  *  ...
x+2M  0 x+2+2M  0  x+4+2M  0  ...
   0  *      0  *       0  *  ...
x+4M  0 x+2+4M  0  x+4+4M  0  ...
   .
   .
   .

どの行にも共通して現れる $x + (x + 2) + (x + 4) + \cdots$ の部分は

初項 $x$
階差 $2$

の等差数列の和で、項数は $\lceil (D - C) / 2 \rceil$ なので $O(1)$ で求められる。

$M$ が含まれる項の総和は

$A$ 行目: $0$
$A + 2$ 行目: $2M \times \lceil (D - C) / 2 \rceil$
$A + 4$ 行目: $4M \times \lceil (D - C) / 2 \rceil$
...

なので $0 + 2M + 4M + \cdots$ がわかればよく、これも等差数列の和。

提出: https://atcoder.jp/contests/abc269/submissions/34955958

ikd

ABC 271 E - Subsequence Path

dp[i][v] := E[1], ..., E[i] まで考えたとき頂点 1 から頂点 v への最短距離

dp[i][*] → dp[i + 1][*] の遷移:

dp[i + 1][v] = dp[i][v]
辺 E[i] を (a, b, c) として、chmin(dp[i + 1][b], dp[i][a] + c)
- 辺 E[i] を使うときだけ最短距離が更新されうる

DP 配列の次元を削減するテク (?) で dp[i][v] を dp[v] と管理すれば (1) の遷移がなくなり、空間 O(N), 時間 O(K) で解ける

提出: https://atcoder.jp/contests/abc271/submissions/35334583

ikd

ARC 149 A - Repdigit Number

答えの候補が少ないので全探索。

実際、桁数をたとえば 4 に固定すると、どの桁の数字も同じという条件から

1111
2222
...
9999

の 9 つのみ考えればよい。桁数 1 〜 N まで考えても全部で 9N 個。

ただ、素朴に 11111...11 などを文字列として持つと、数字の個数が合計で N^2 になる。いまは M で割った余り 11111...11 mod M だけあればよく、桁数が大きい数でも下から 10 倍しながら M による剰余を計算していける。余りは M 未満になるので 64bit 整数に収まる。

このように答えの候補 (を M で割った余り) を列挙して、桁数の大きい順、数字の大きい順に見ていき mod M が 0 のものに初めて出会ったところで答えを出力すればよい。

提出: https://atcoder.jp/contests/arc149/submissions/35375626

ikd

ABC 276 F - Double Chance

$K$ に対する答えは、期待値の定義からこうなる。

\frac{\sum_{i = 1, 2, \dots, K} \sum_{j = 1, 2, \dots, K} \max(A_i, A_j)}{K^2}

$K$ が $1$ 増えたときの差分を求める。

$\left[ \left[ \sum_{i = 1, \dots, K} \sum_{j = 1, \dots, K} \max(A_i, A_j) \right] + \clubsuit \right] / (K + 1)^2$ の $\clubsuit$ 部分を求める。

$A_{K + 1}$ の期待値への寄与を考えると $\clubsuit$ は $2 \sum_{i = 1, \dots, K} \max(A_i, A_{K + 1}) + A_{K + 1}$ となる。

1 回目の操作で引くカード $A_i$	2 回目の操作で引くカード $A_j$
$A_{K + 1}$	$A_{K + 1}$ 以外
$A_{K + 1}$ 以外	$A_{K + 1}$
$A_{K + 1}$	$A_{K + 1}$

$\sum_{i = 1, \dots, K} \max(A_i, A_{K + 1})$ はよくあるパターンで、 $\max(A_i, A_{K + 1})$ が $A_{K + 1}$ 以上かどうか分けて考えると

$A_{K + 1}$ 以上の $A_i$ についての総和 $\sum A_i$
( $A_{K + 1}$ 未満の $A_i$ の個数) × $A_{K + 1}$

の和になる。これは Segment Tree や Fenwick Tree で $K = 1, 2, \dots, N - 1$ に対して高速に計算できる。

提出: https://atcoder.jp/contests/abc276/submissions/36265759

ikd

ABC 277 F - Sorting a Matrix

列の入れ替え操作によって各行をソート済みにできるか、という問題の解法をメモ。

A が

3 3 1
5 4 4
9 8 6

であるケースを考える。

たとえば 1 行目 [3, 3, 1] について、列の入れ替えによって

1 列目は 3 列目より後
2 列目は 3 列目より後

に動かす必要がある。このような制約が 2 行目, ...., H 行目についても同様に課される。

この問題は以下のグラフが DAG かどうか、つまり、トポロジカルソートができるかを判定すれば解ける。

頂点
- 頂点 1: 「1 列目」を表す頂点
- ︙
- 頂点 W: 「W 列目」を表す頂点
辺
- 「u 列目は v 列目より後」という制約に対して有向辺 u -> v を張る

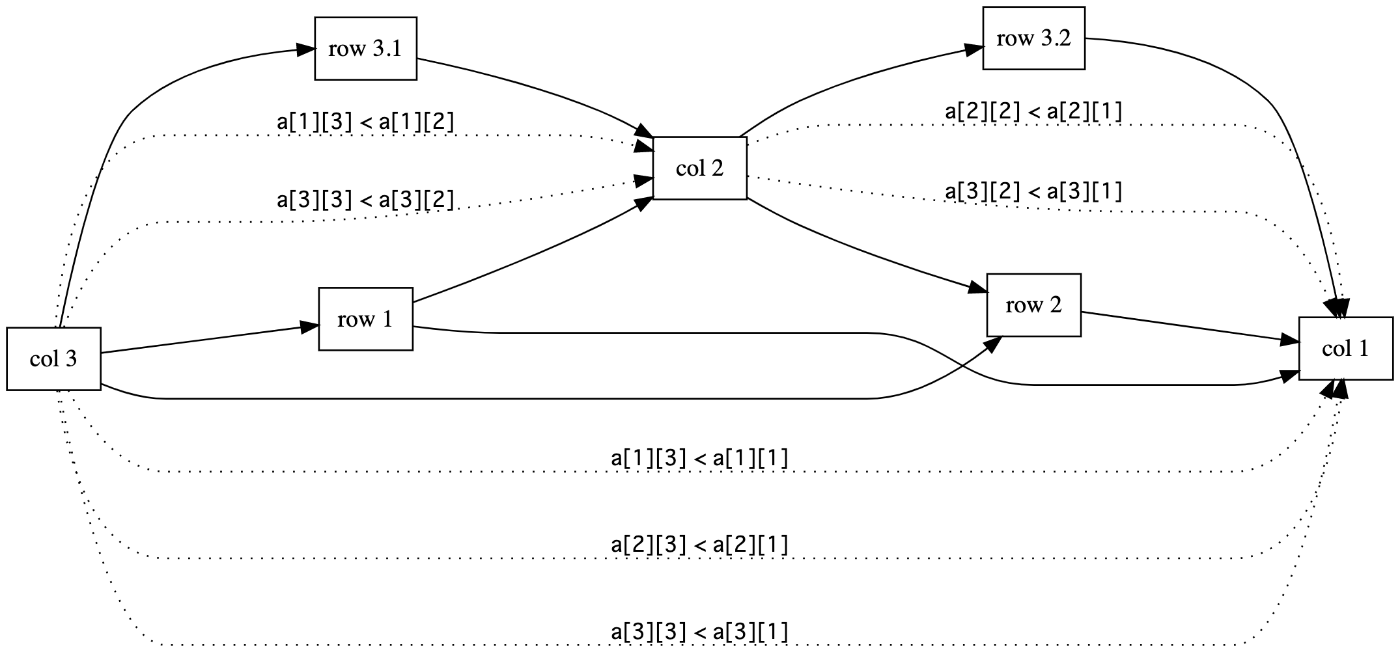
たとえば上の A においては次のグラフが対応する。この場合、頂点 3 → 頂点 2 → 頂点 1 がトポロジカル順序とわかる。

グラフ

ただ、「u 列目は v 列目より後」という制約の個数 = 辺の本数は Ω(HW^2) になる。そこで、必要な辺のみを含むグラフを構築して DAG 判定をする。

素朴な (上に書いた) グラフ構築手順では A の 3 列目 [9, 8, 6] から、以下の制約

(α) 1 列目は 2 列目より後
(β) 2 列目は 3 列目より後
(γ) 1 列目は 3 列目より後

に対応する辺を張ることになる。しかし、この例だと (α), (β) のみでよく (γ) は不要。

この要領 (くわしくは公式解説) でグラフを構築すると頂点数と辺数が O(HW) に抑えられる。上の A に対応するグラフは次の図の実線部分になる。

辺数を削減したグラフ

提出: https://atcoder.jp/contests/abc277/submissions/36471301

ikd

ABC 283 E - Don't Isolate Elements

PAST の過去問 https://atcoder.jp/contests/past202010-open/tasks/past202010_n と同様の DP

ikd

ARC 153 B - Grid Rotations

縦横独立に考えられるので 1 次元の列に対して区間の反転操作を高速にできればよい。この記事 https://xuzijian629.hatenablog.com/entry/2018/12/08/000452 のデータ構造を使うとできる。

ikd

ABC 307 E - Distinct Adjacent

包除原理で解くことを考える。

$K = 1, 2, \dots, N - 1$ に対して、「同じ数を渡された隣り合う組が $K$ 以上」となる場合の数が分かればよい。これは $N$ 頂点が環状に並んだ状態から、隣り合う頂点同士を辺でつなぐことを $K$ 回おこなったあとの連結成分数を $c$ として $\mathrm{choose}(N, K) \times M^c$ になる。二項係数 choose(N, K) は辺のつなぎ方、M^c は各連結成分内で 1 〜 M どの数にするかに対応している。

K 本の辺のつなぎ方に応じて、連結成分数が変わるかと勘違いしていたけどそんなことはなかった。c = N - K で一定。

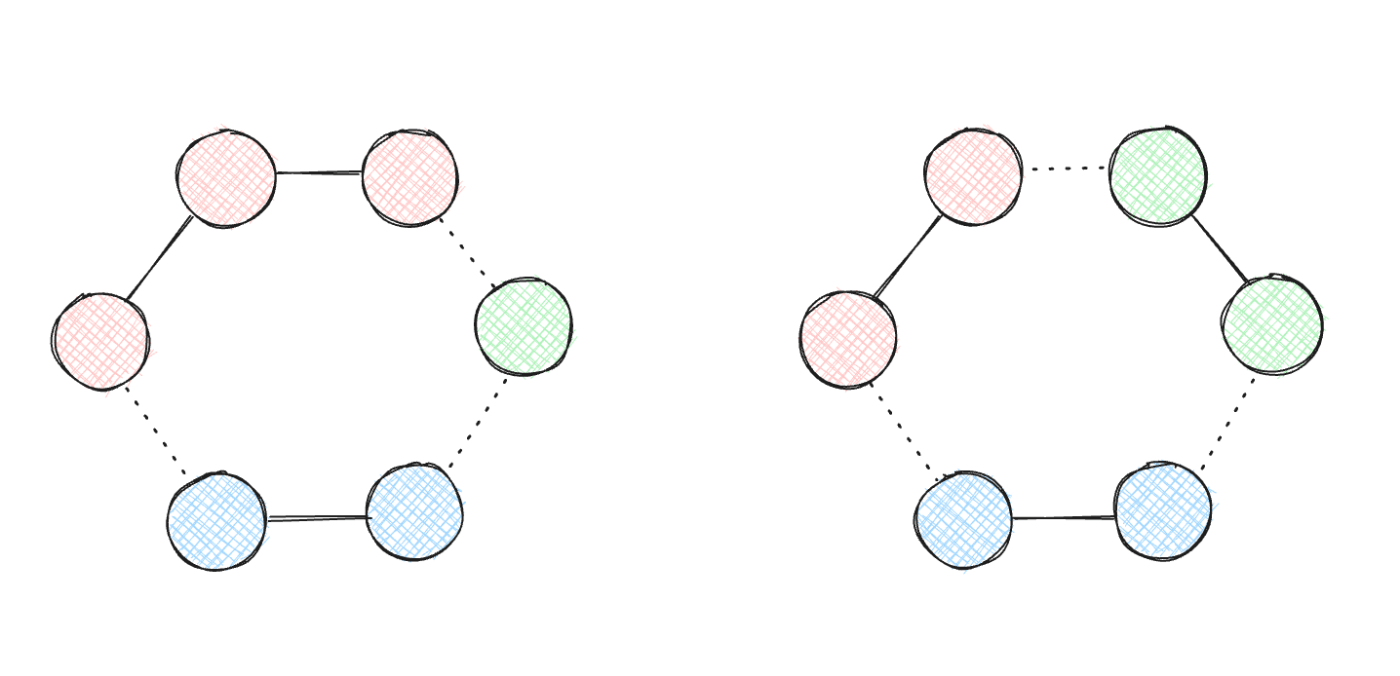
N = 6, K = 3, c = 3 の例

ikd

頻出らしいのでメモ。

ふたつの整数列 $A, B$ が与えられる。「 $i, j$ をえらんで $A_i \leftarrow A_i - 1, A_j \leftarrow A_j + 1$ と更新する」という操作をおこなえる。 $A = B$ にするための最小操作回数は？

まず sum(A) = sum(B) が必要。このとき答えは $(\sum_{i = 1}^N \mathrm{abs}(A_i - B_i))/2$ になる。

ikd

ARC 167 B - Product of Divisors

$A$ の素因数分解を $A = p_1^{e_1} p_2^{e_2} \cdots p_n^{e_n}$ とする。

「 $A^B$ の正の約数の総積 $P$ を $A$ で最大何回割れるか」は $P$ を $p_i^{e_i}$ で割れる回数の ( $i = 1, 2, \dots, n$ にわたる) 最小値。

$P$ における $p_i$ の指数を調べよう。 $A^B$ の約数における $p_i$ の指数ごとに考えてまとめあげればいい。

$A^B$ の約数のうち $p_i$ の指数が $1$ の項は $\prod_{j \ne i}(e_jB + 1)$ 個ある
- $p_i$ 以外の素因数の指数は $0$ から $e_\star B$ まで独立に動くので
- (よくわからなくなったら小さい $A, B$ で確かめてください)
$p_i^2$ も同じだけある
$\vdots$
$p_i^{e_iB}$ も同じ

結局 $P$ における $p_i$ の指数は $(1 + 2 + \cdots e_iB) \prod_{j \ne i}(e_jB + 1)$ となる。前半は等差数列の和で $e_iB(e_iB+1)/2$ と書ける。

ikd

ABC 328 F - Good Set Query

「頂点 u と頂点 v の『差』が w」の関係を保ちつつ頂点集合をマージする問題。

diff[v] := (親 p の値) - (自身 v の値) を管理する UnionFind で解ける。「値」は「重み」とも呼ばれる。

頂点 v に対する Find 操作後には diff[v] = (根 r の値) - (自身 v の値) となる必要がある。この値は親を辿る過程で diff の累積和をとっておくことで求められる。

Union 操作：TODO あとで図を描く。

提出コード：https://atcoder.jp/contests/abc328/submissions/47511009

ikd

ABC 341 E - Alternating String

平方分割。

入力の 0/1 数列を $\sqrt{N}$ 個の区間 (ブロック) に分割する。各ブロックの長さは $\sqrt{N}$ にする。

ブロックごとに

全要素を反転させるかのフラグ flip
隣接要素が異なる個数 ( $S_i \neq S_{i + 1}$ の個数) diff
- (オーバーキルな気がするので「隣接要素がすべて異なるか」だけでもいいかも)

を管理する。

反転クエリ
- ブロック全体への適用：flip の真偽を反転させる、diff は変わらない
- ブロックの一部への適用：flip の効果を全要素に伝搬して、あとは要素をひとつずつ処理する、diff を定義通りに再計算する
判定クエリ
- 「直前のブロックの最後の要素 (0 or 1)」を持って、クエリ対象のブロックを左から見ていくと答えられる
- ブロックの「境界」の要素が異なる個数 + 各ブロックの diff の総和を計算できる
  - → クエリで与えられた区間の幅と比較して Yes or No がわかる

N = 16, 判定クエリが [3, 13] に来たときの例

提出コード：https://atcoder.jp/contests/abc341/submissions/50494167

ikd

ABC360 G - Suitable Edit for LIS

変更する場所 x をすべて試して LIS の長さの max を取る。

A[1] は -∞
A[N] は +∞

に変更するのが最適なので 1 < x < N を考える。

A[x - 1] と A[x + 1] の間に「隙間」があると LIS を伸ばせそう。

A[x - 1] + 1 < A[x + 1] のとき A[x] を A[x - 1] + 1 とおけば、

A[1], A[2], ..., A[x - 1] の LIS のうち、A[x - 1] で終わるもの (▲)
A[x]
A[x + 1], ..., A[N] の LIS のうち、A[x + 1] で始まるもの (■)

をこの順につないだ列は A[1], ..., A[N] の LIS になる。

LIS (▲) の長さは dp をセグメント木で高速化して LIS を求めるよくあるやり方で分かる。(■) も同じようにして分かる。