ドドスコするオートマトン考
はじめに
ある日 twitter に問題が降ってきてちょっとした熱狂がありました。
"ドド" と "スコ" からなるランダムな入力を受け付けて、"ドドスコスコスコ" が連続で3回ならんだら「ラブ注入♡」を出力して終了する、という問題。
いろんな言語で書かれて、Golf的に短いものとか、グラフィカルなものとか夏休みの自由研究という感じで面白いものがたくさんあったの[1]ですが、やっぱり最初に思いつくのは有限オートマトンですよね。
手で書いてみる
入力の種類が「ドド」と「スコ」しかなくて、"ドドスコスコスコ"を3回受け付けたら受理状態になるオートマトンなので、単純に手で書けそうです。

3回受け付ける、とありますが、カウンタを用意して、"ドドスコスコスコ"の回数をカウントする必要はありません。状態を増やして対応してしまいましょう。
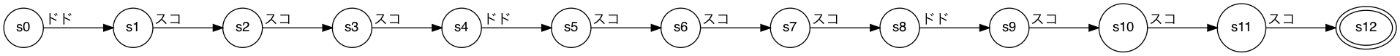
ここまでうまくいく場合だけのケースで辺を追加していましたが、ここに失敗するときの辺を追加してやります。
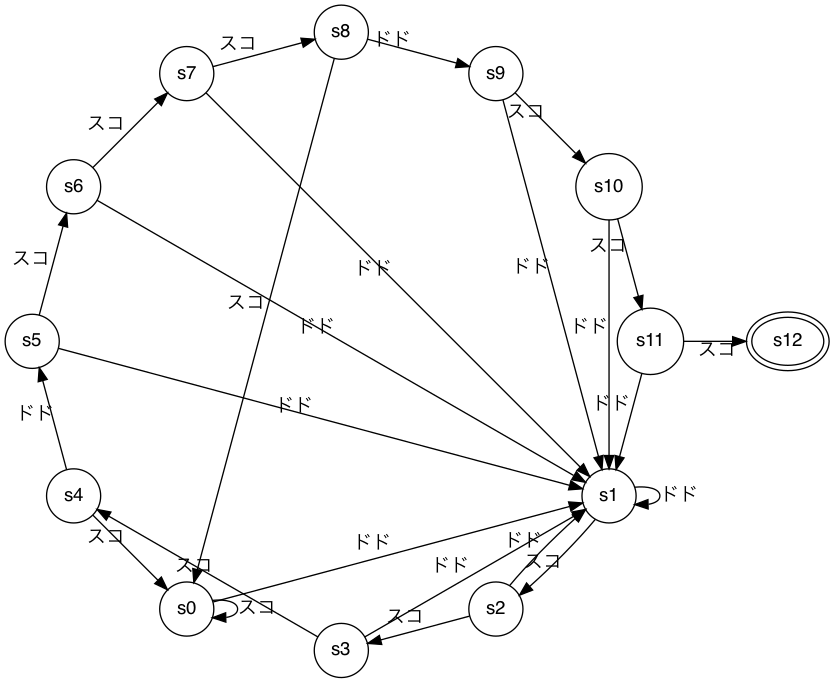
これで完成です。
オートマトンの構造
オートマトンは次のように5つ組で定義されます。たぶん正確には決定性[2]有限[3]オートマトンと呼ばれるやつです。
Q: 状態の集合
これだけです。上の例と対応させるとこんな感じです。
| オートマトンの項目 | ドドスコ | 補足 |
|---|---|---|
| s0, s1, ... | グラフのノード(丸のところ) | |
| "ドド" と "スコ" | 入力の種類 | |
| 「状態と入力のペア」と次の状態 |
|
|
| s0 | 初期状態。開始時の状態のこと | |
| 受理状態。オートマトンのゴールみたいなもの。ドドスコでは受理状態は |
状態
状態遷移は、「状態と入力のペア」から次の状態への関数ですが、要するに「今の状態と入力のペア」から次の状態が分かればいいので map で表現できます。

type pair struct {
State State
Input string
}
var transition = map[pair]State{
{State: s0, Input: "ドド"}: s1,
{State: s1, Input: "スコ"}: s2,
{State: s2, Input: "スコ"}: s3,
{State: s3, Input: "スコ"}: s4,
....
Go は map のキーに構造体を取れるので、ここに状態と入力のペアが取れて便利。
動かしてみる
状態遷移はこんな感じです。
var transition = map[pair]state{
{state: s0, input: "ドド"}: s1, {state: s0, input: "スコ"}: s0,
{state: s1, input: "スコ"}: s2,
{state: s2, input: "スコ"}: s3,
{state: s3, input: "スコ"}: s4,
{state: s4, input: "ドド"}: s5, {state: s4, input: "スコ"}: s0,
{state: s5, input: "スコ"}: s6,
{state: s6, input: "スコ"}: s7,
{state: s7, input: "スコ"}: s8,
{state: s8, input: "ドド"}: s9, {state: s8, input: "スコ"}: s0,
{state: s9, input: "スコ"}: s10,
{state: s10, input: "スコ"}: s11,
{state: s11, input: "スコ"}: s12,
}
なんか数が足りないなと思った方は鋭いです。s0 に遷移する状態を端折っています。
s1 を 0 として定義しているので、map になければゼロ値で s1 になるので端折っています。
もちろんちゃんと書いてもいいです(それが正しい)。
実行部分はこんな感じ:
func acceptor(ctx context.Context, ch <-chan string, w io.Writer) bool {
q := start
for {
select {
case v, ok := <-ch:
if !ok {
return false
}
q = transition[pair{state: q, input: v}]
fmt.Fprint(w, v)
if q == accept {
fmt.Fprintln(w, "ラブ注入♡")
return true
}
case <-ctx.Done():
return false
}
}
}
ランダムな入力がチャンネルから入ってくるので、受け取って、状態遷移をチェックします。
もし状態が accept(=s12) なら「ラブ注入♡」して終わります。
並びがそろわないと延々と終わらない可能性があるので、ctx を受け取って、timeout 出来るようにしています。
また、入力がなくなってしまったときも終了します。

※ 着色はわかりやすさのためにターミナルでマッチさせてます
これライブラリ化しといたら便利では?
ちょっとしたマッチングとかするときに、小さなオートマトンを書けるようにしておいたら便利では?と思って
ライブラリかしてみました。入力が文字列でなくても、比較可能でさえあればいいので、ジェネリクスの comparable を使って対応してみました。
オートマトンの実行中に何か作業を差し込めれば便利なので、適当に関数を取れます。
ドドスコはこんな感じで書けます。
a := automaton.New(start, transition, final)
ok, err := a.Run(ctx, ch, func(_ automaton.State, in string, q automaton.State) {
fmt.Printf(in)
if a.Final(q) {
fmt.Printf("ラブ注入♡")
}
})
便利・・・ですかねぇ。
おわりに
ちょっと思い立って書いてみたらよくわからん数のイイネをいただいたので、勢いにまかせていろいろやってみました。
有限オートマトン、計算機科学の基礎でやるけどなんのこっちゃい、と思われてる方も多いかも知れませんが、5つの要素を分かってるだけで構築できていろいろ便利なので、是非遊んでみて下さい。
Happy hacking!

Discussion