これは「マルチボディダイナミクス(2) ー数値解析と実際ー」コロナ社 のp.4 (2) 並進ジョイントの内容を理解するためにまとめ直したものです。
並進ジョイントは2つのボディの方向が常に等しく、軸に沿った移動しかできない拘束のことです。
拘束条件式
並進ジョイントの拘束条件は、それぞれのボディの角度が常に同じであることなので、ボディの角度を \theta_i , \theta_j とすると
\theta_i-\theta_j-(\theta_i^0-\theta_j^0)=0
となります。ここで上付き添え字の0は初期位置をあらわし、両ボディは初期値の角度を保ったまま常に同じでなくてはなりません。
また角度が同じでも位置がずれると拘束軸に沿わなくなるので、拘束軸のベクトル \vec{s_i} と、両ボディの拘束点を結んだベクトル \vec{d_{ij}} は平行であるという条件も必要になります。このことは \vec{s_i} に垂直なベクトル \vec{n_i} を用いると、\vec{n_i}\perp\vec{d_{ij}} と表すことができて、式にするとこれは内積が0という条件なので
\vec{n_i}\cdot\vec{d_{ij}}=0
となり、xy 成分で表すと
(x_i^P-x_i^Q)(y_j^p-y_i^P)-(y_i^P-y_i^Q)(x_j^P-x_i^P) = 0
となります。よって並進ジョイントの拘束条件式は次のようになります。
\begin{bmatrix}
(x_i^P-x_i^Q)(y_j^p-y_iP)-(y_i^P-y_i^Q)(x_j^P-x_i^P) \\
\theta_i-\theta_j-(\theta_i^0-\theta_j^0)
\end{bmatrix} = 0
ヤコビアン
次に、拘束条件式を偏微分してヤコビアン J にすると
| \partial x_i |
\partial y_i |
\partial\theta_i |
| (y_i^P-y_i^Q) |
-(x_i^P-x_i^Q) |
-(x_j^P-x_j)(x_i^P-x_i^Q) \\ -(y_j^P-y_j)(y_i^P-y_i^Q) |
| 0 |
0 |
1 |
| \partial x_j |
\partial y_j |
\partial \theta_j |
| -(y_i^P-y_i^Q) |
(x_i^P-x_i^Q) |
(x_j^P-x_j)(x_i^P-x_i^Q) \\ +(y_j^P-y_j)(y_i^P-y_i^Q) |
| 0 |
0 |
-1 |
ベクトル表記だと
J =
\begin{bmatrix}
\vec{QP_{i}y} & -\vec{QP_{i}x} & -\vec{O'P_j}\cdot\vec{QP_i} &
-\vec{QP_{i}y} & \vec{QP_{i}x} & \vec{O'P_j}\cdot\vec{QP_i} \\
0 & 0 & 1 & 0 & 0 & -1
\end{bmatrix}
これを拘束方程式の
JM^{-1}J^T\lambda\Delta t+J(u+M^{-1}F\Delta t)
に入れて \lambda を求めます。
具体例
ワールド座標系に固定された ボディI の軸に、ボディJ が拘束されている状態を計算します。
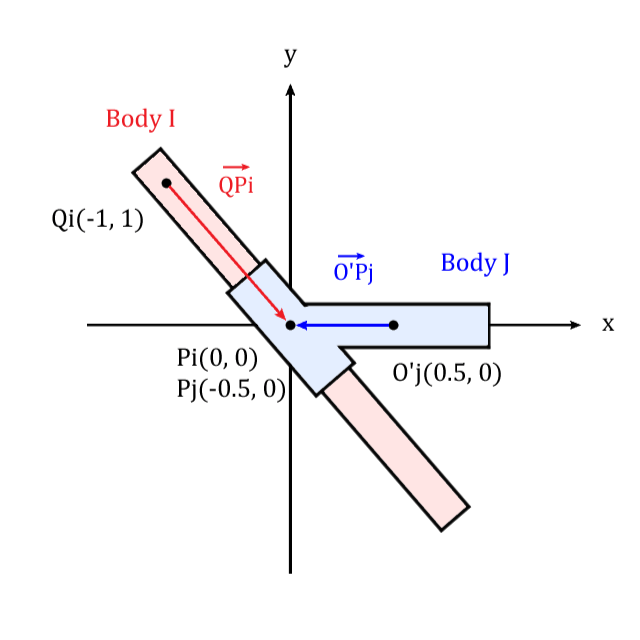
拘束条件を表すにはボディI 上で拘束軸を表す2点 P_i,Q_i と、拘束軸上のボディJ の点 P_j の座標が必要になります。点 O'j はボディJ の原点です。
ボディJのパラメータは次のとおり。計算結果を見てわかるようにできるだけ単純にしておきます。
| パラメータ |
値 |
| 質量 |
1 kg |
| 長さ |
1 m |
| 初期座標 |
(0.5, 0) |
| 初期角度 |
0 |
| 慣性モーメント |
1/3 |
ボディI はワールド座標に固定しているので、ボディJの拘束条件式を解いていきます。まずヤコビアンを求めます。
J = \begin{bmatrix}
-(y_{i}^P-y_{i}^Q) & (x_{i}^P-x_{i}^Q) & \begin{gather}(x_j^P-x_j)(x_i^P-x_i^Q) \\ +(y_j^P-y_j)(y_i^P-y_i^Q)\end{gather} \\
0 & 0 & -1
\end{bmatrix} =
\begin{bmatrix}
1 & 1 & -0.5 \\
0 & 0 & -1
\end{bmatrix}
質量の逆数マトリクス M^{-1} は
M^{-1} = \begin{bmatrix}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 3
\end{bmatrix}
ここから A マトリクスを求めると
A = JM^{-1}J^T = \begin{bmatrix}
1 & 1 & -0.5 \\
0 & 0 & -1 \end{bmatrix}
\begin{bmatrix}1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 3\end{bmatrix}
\begin{bmatrix}1 & 0\\ 1 & 0\\ -0.5 & - 1\end{bmatrix} =
\begin{bmatrix}2.75 & 1.5 \\ 1.5 & 3\end{bmatrix}
次に方程式の右辺 b = J(u+M^{-1}F\Delta t) を求めます。u は速度、F は外力です。
u = \begin{bmatrix}0 \\ 0 \\ 0\end{bmatrix},
F = \begin{bmatrix}0 \\ -9.81 \\ 0\end{bmatrix}
ここから \Delta t = 0.01 とすると
b = \begin{bmatrix}1 & 1 & -0.5\\ 0 & 0 & -1\end{bmatrix}
(\begin{bmatrix}0\\0\\0\end{bmatrix}+\begin{bmatrix}1&0&0\\0&1&0\\0&0&3\end{bmatrix}
\begin{bmatrix}0\\-9.81\\0\end{bmatrix}\times0.01) =
\begin{bmatrix}-0.0981\\0\end{bmatrix}
方程式 Ax = b (x = A^{-1}b) を解くと
x = \begin{bmatrix}-0.04905\\0.024525\end{bmatrix}
となって、ヤコビアンの転置行列 J^T をかけて元に戻すと拘束力が求まります。
J^Tx = \begin{bmatrix}X軸の拘束力\\Y軸の拘束力\\回転トルク\end{bmatrix}=
\begin{bmatrix}-0.04905\\-0.04905\\0\end{bmatrix}
拘束軸が斜め45度なので、拘束軸に垂直な拘束力がボディJ にかかり軸に沿った動きになることがわかります。

Discussion