Zenn
📏

【競プロ】ダイクストラ法

2024/03/02に公開
競技プログラミング
AtCoder
グラフ理論
アルゴリズム
tech

はじめに

今回は最短経路を求めるアルゴリズムの中でも頻出なダイクストラ法について、お気持ちから実装まで解説したいと思います！

最短経路アルゴリズム比較

アルゴリズム 実行時間 使用するデータ構造 求める最短経路 負の重み 負閉路の検出
BFS O(V + E) キュー 単一始点 x x
ダイクストラ法 O((V+E)\log V) ヒープ（優先度付きキュー） 単一始点 x x
ベルマンフォード法 O(VE) 配列またはリスト 単一始点 o o
フロイド-ワーシャル法 O(V^3) 行列 全頂点間 o o
  • BFS: 重みなしグラフにおける単一始点最短経路を求めるのに使用される。
  • ダイクストラ法: 重み付きグラフにおける単一始点最短経路を求めるのに使用される。負の重み付き辺には対応していないが、非負の重み付きグラフでは効率的。最短経路が木構造となる。負の閉路の検出には使えない。
  • ベルマンフォード法: 負の重み付き辺を含むグラフにおける単一始点最短経路を求めるのに使用される。負の閉路が存在する場合は検出できる。遅いが、負の重みに対応している。
  • フロイド-ワーシャル法: すべての頂点間の最短経路を求めるのに使用される。負の重み付き辺を含むグラフにも対応している。計算量は大きいが、密なグラフや辺の数が少ない場合に有用。

アルゴリズム

お気持ち

始点から最短で行けるところを探索していくイメージです。
アルゴリズムとしては優先度付きキューを用いて、始点からの暫定距離が小さい順に点を取り出せるようにします。
取り出した点から到達できる点に対して、暫定距離を再計算してキューに格納します。
キューが空になったら終了です。

擬似コード

始点をstartとする

  1. 暫定距離を表す配列distを距離の最大値で初期化
  2. 距離が小さいものを優先する優先度キューを用意
  3. キューに、距離と頂点のペア(0, start)を追加
  4. キューが空になるまで、以下の操作を繰り返す
    • キューの先頭(d, v)を取り出す
    • 距離dが暫定距離dist[v]より大きければ3.に戻る
    • そうでなければ、この頂点vから到達できる頂点nに対して以下の操作をする
      • vからnに移動したときの距離が暫定距離dist[n]より大きければ何もしない
      • そうでなければ、キューに距離と頂点のペアを追加
動作例

赤：確定、黒：未確定、青：更新候補

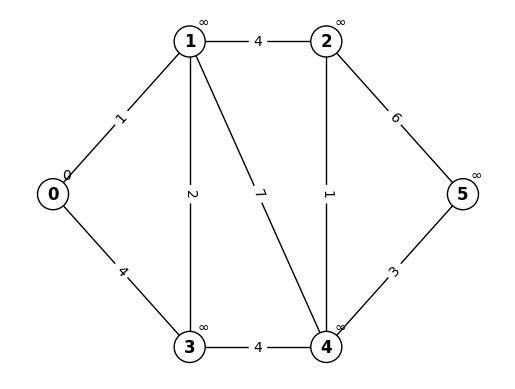
STEP.0

始点0の暫定距離を0、それ以外をINFと初期化

キュー
(0,0)

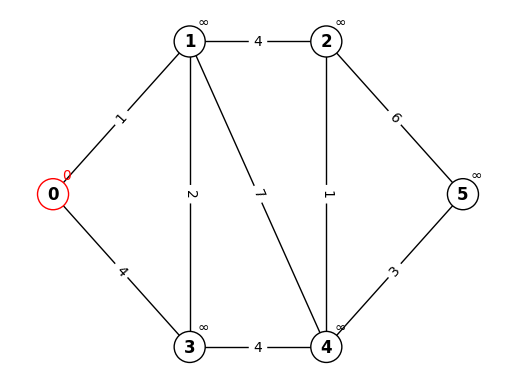
STEP.1

確定していない点（赤以外）から暫定距離が最小のものである点0を確定

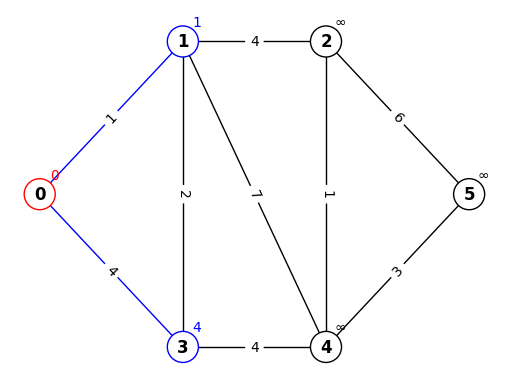
確定した点0の隣接する点(1,3)の暫定距離を更新

キュー
(1,1)
(3,4)

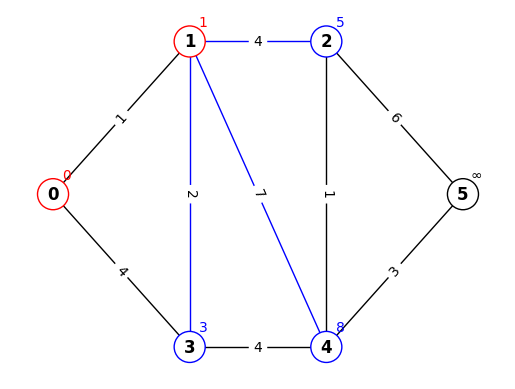
STEP.2

確定していない点（赤以外）から暫定距離が最小のものである点1を確定

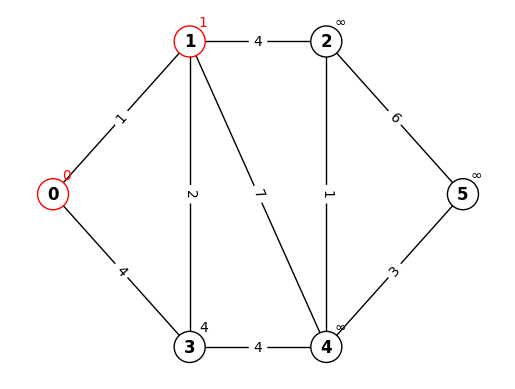
確定した点1の隣接する点(2,3,4)の暫定距離を更新

キュー
(3,3)
(3,4)
(2,5)
(4,8)

STEP.3

確定していない点（赤以外）から暫定距離が最小のものである点3を確定

キュー(3,4)は点3が確定しているためスキップ
確定した点3の隣接する点(4)の暫定距離を更新

キュー
(2,5)
(4,7)
(4,8)

STEP.3

確定していない点（赤以外）から暫定距離が最小のものである点2を確定

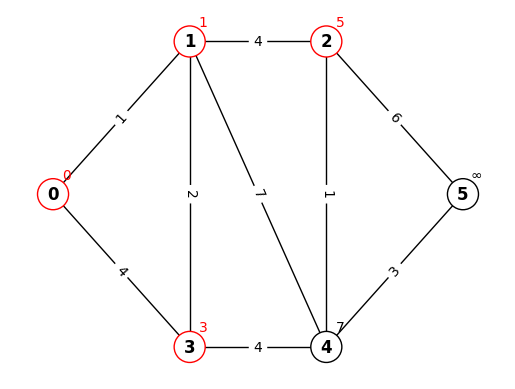
確定した点2の隣接する点(4,5)の暫定距離を更新

キュー
(4,6)
(4,7)
(4,8)
(5,11)

STEP.3

確定していない点（赤以外）から暫定距離が最小のものである点4を確定

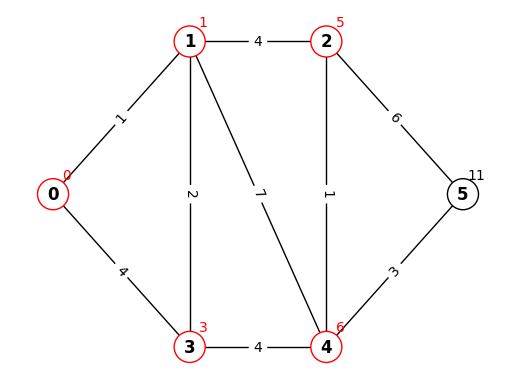
キュー(4,7),(4,8)は点4が確定しているためスキップ
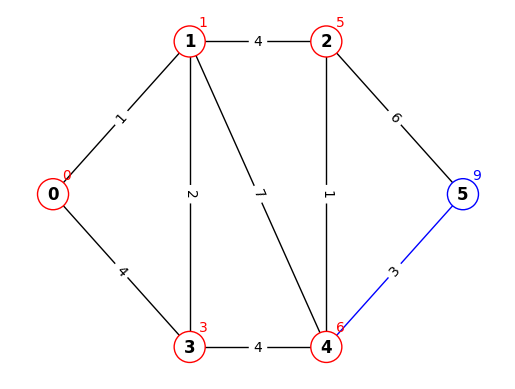
確定した点4の隣接する点(5)の暫定距離を更新

キュー
(5,9)
(5,11)

STEP.3

確定していない点（赤以外）から暫定距離が最小のものである点5を確定

(5,11)は点5が確定しているためスキップ
全ての点が確定したので終了

コード

dijkstra
struct Edge{
    long long to;
    long long cost;
    // その他、必要な情報があれば要素を追加
};
using Gpaph=vector<vector<Edge>>; // 隣接リストを表す型
using Pair = pair<long long, long long>; // 距離と頂点のペアを表す型
vector<long long> dist; // 暫定距離を格納する配列
const long long INF = 1LL << 60;

void dijkstra(const Graph& G, vector<long long>& dist, long long start){
  priority_queue<Pair,vector<Pair>,greater<Pair>> Q;
  dist.assign(G.size(),INF);
  Q.emplace(dist[start]=0,start); // dist[start]=0をして、qに(0,start)をpush

  while(!Q.empty()){
    Pair q=Q.top();
    Q.pop();
    long long d=q.first;
    long long v=q.second;

    if(d>dist[v]) continue;

    for(const auto& edge:G[v]){
      long long nextdist = d+edge.cost;
      if(nextdist<dist[edge.to]){
        Q.emplace(dist[edge.to]=nextdist,edge.to);
      }
    }
  }
}
使用例
main
int main() {
  long long N; cin>>N;
  Graph G(N);
  for(long long i=0; i<N-1; i++){
    long long a,b,x; cin>>a>>b>>x;
    Edge A={i+1,a},B={x-1,b};
    G[i].push_back(A);
    G[i].push_back(B);
  }

  vector<long long> dist;
  dijkstra(G,dist,0);

  cout<<dist[N-1]<<endl;
}

解説

辺を表す構造体: Edge

Edge
struct Edge{
    long long to;
    long long cost;
    // その他、必要な情報があれば要素を追加
};

（有向）辺を表す構造体を定義する。
toは辺の終点、costは重みを表す。始点を表すfromは隣接リストを用いるため不要。

使用例
    Edge e={3,100}; // 構造体で定義した順番に代入される

    cout<<e.to<<endl; // 3
    cout<<e.cost<<endl; // 100

隣接リストを表す型: Graph

Gpaph
using Gpaph=vector<vector<Edge>>;

各頂点に対して、Edgeを格納した配列を値に持つ配列（隣接リスト）としてGraph型を定義する。

使用例
long long N=3; // 頂点数
Graph G(N); // 頂点数で初期化
Edge e1={1,100}; // 終点1,重み100の辺を定義
Edge e2={2,100}; // 終点2,重み200の辺を定義
Edge e3={2,300}; // 終点2,重み300の辺を定義

G[0].push_back(e1); // 始点0,終点1,重み100の辺のデータを格納
G[0].push_back(e2); // 始点0,終点2,重み200の辺のデータを格納
G[1].push_back(e2); // 始点1,終点2,重み300の辺のデータを格納

for(long long i=0; i<N; i++){
    for(auto edge:G[i]){
        cout<<i<<" to "<<edge.to<<", weight: "<<edge.weight<<endl;
    }
}
// 0 to 1, weight: 100
// 0 to 2, weight: 200
// 1 to 2, weight: 300

参考

https://qiita.com/ageprocpp/items/cdf67e828e1b09316f6e

Discussion