よわよわ緑コーダーだけど入水したい

y

なんとか入水したい。問題の記録など。
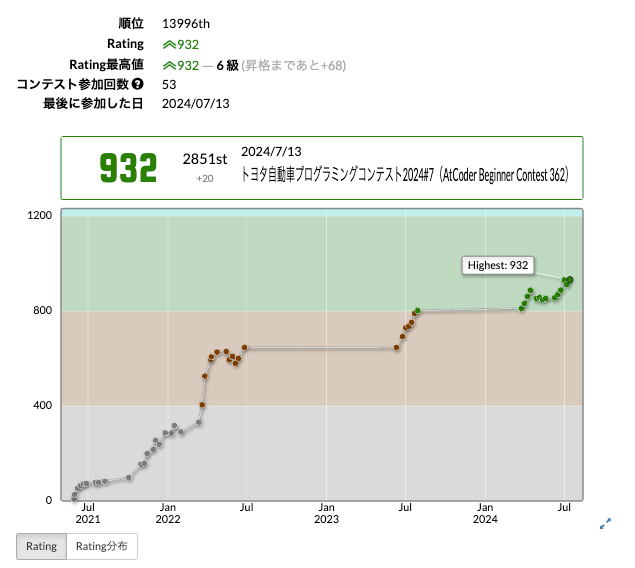
現在のレート(2024/7/15)
2024/7/15のレート

y

PAST1_M

6/22 PAST本1-1より．

A~Dなどをllで持っていたせいでcheck関数内でdoubleが変なことになっていたっぽい．1WA
二分探索の探索範囲について
- 範囲で回す方法でしか解いたことがなかった．小数だけど絞り込みどうするんだろう？と思ったので覚えておく．
- 誤差で見る方法もある：許容が1e6なのでright-left<0.000001でもOK
式変形がパッと思いつかなかった．
- いったん詰まったら数学的にできないか考えてみたい．（苦手で避けがちなので．）

y

ABC207_C

灰diffだけど詰まってしまったので。

開区間の時に+-0.5をすることで大小のみで共通部分を求められるようにしている
max(l1,l2)<=min(r1,r2)で共通部分を求められる。
- 開始地点より小さい終了地点が存在しない。
  - もう一方の区間が始まる前に一つの区間が終了してしまわないように。

y

ABC214_C

これ灰diffは嘘じゃない？
案の定シミュレーションして $O(N^2)$ でTLEからの解法AC。
priority_queueの使い方上手いな〜と思ったので記録。スムーズに使えるようになりたいね！

y

ABC218-C

理論はわかるがとにかく実装が辛い。
- ちゃんと紙とペンを用意して立式した方がいい。
- 自前でテストケースを用意できるようになりたい。多分ICPCとかでも効いてくる。
こういうのをサクッと解けるようになりたい。

y

ABC361-D

コンテスト中にスルーしてしまったが案外簡単そうだったので。
BFS一回集中的にやろうかな。
1WA: 最初からS==Tのケースの考慮漏れ。

y

ABC361

本番で通せなかった問題。
考察の大筋は合ってた。これ頑張れば本番通せたな〜〜悔しい
木の直径をスムーズに求められるように。(https://atcoder.jp/contests/abc361/editorial/10329)

y

ABC225-C

灰diffだがやたら引っかかってしまった。

7行をはみ出るケース
列を(B-1)/7にしなければならないのにB/7にして変なところで改行が挟まるような形にしてしまった。

こういうので落としたくないな〜〜〜〜〜

今回はどっちにしろ位置を間違えていたので違っただろうけど、解説のようにB[0][0]の基準が何番目か求めて、以降もB[i][j]が元の行列の何番目にいたかを見たほうが楽かも。

y

ABC222-C

解説読んでなるほどなーってなったが、実装でもバグり散らしていた。
点数で勝敗、同点時に順位順になる時にpair<ll,ll>で持たせておいて試合ごとに点数のみ更新し、ラウンドごとにsortすると良い

y

ABC224-C

解説の面積の公式覚えておく
$(x_1,y_1),(x_2,y_2),(x_3,y_3)$ の面積は、
$S = \frac{1}{2}|(x_2-x_1)(y_3-y_1)-(x_3-x_1)(y_2-y_1)|$

y

ABC238-C

modintの割り算

$a/b$ ： $a$ に $b$ の逆元をかけると得られる
「998244353 で割ったあまり」の求め方を総特集！〜逆元から離散対数まで〜

modintの扱いはバグらせがちなので慎重に

y

ddcc2020_qual-C

長方形に切り分ける問題。
解説のシミュレーションが綺麗だった。

いちごにナンバリング
自分より左のナンバリングされてないマスを全て自分のナンバーに割り当て
- 右のマスも同様に行う→いちごがある行は全て割り当て済みに
次に上下でも同様に行う
- 横にいちごがある行はすでに割り当て済みで、割り当ててないマスの行は必ず全て割り当てられていない
  →上下を見た時に長方形が干渉しない！

y

ABC263-C

next_permutationの使い方上手すぎる
- M個の要素でN個選んで昇順に出力→N個の0とM-N個の1で0のindex+1を出力
解説のDPの方の解全然わからん。読む

y

ABC266-C

外積で3点の座標から角度を見る
- https://atcoder.jp/contests/abc266/editorial/4659

点 $O,A,B$ について $\angle AOB<180$ になる( $O$ を中心とする円で反時計回りに $A,B$ の順で並ぶ)のは $A_xB_y-A_yB_x>0$ の時

Rustが使いたくなったのでRustで解いてみた。意外と快適？

y

ABC265-D

累積和+にぶたんで連続する3区間の和がどうなるかを調べる。想定回通り。
解説に興味深い記述があった。

実装上は $S$ をsetで保持することで、明示的に二分探索を行う必要がなくなります

累積和をsetで持たせておいて，xを $x$ までの和とすることで累積和でx+pのものが存在すればそうなるような $y$ が存在，...と言うようなことをしている。
- 単調増加よりx+pがあれば必ずxから連続で和が $P$ の区間になる。

for(auto x:s){
    if(s.find(x+p)!=s.end() && s.find(x+p+q)!=s.end() && s.find(x+p+q+r)!=s.end()){
        cout << "Yes" << endl;
        return 0;
    }
}

y

ABC269-C

1<<(nの桁数+1)での全探索しようかと思ったけど判定とかの計算量もあるし無理くない...？とか思ってました。解法AC。
集合を利用。 $N$ の $i$ 桁目が $1$ の時に、今までの条件を満たすものの $i$ 桁目を $1$ にしたものを加える。
- 答えとなる条件は" $i$ 桁目が $1$ の時 $N$ の $i$ 桁目が $1$ である"なので必ずこれを満たす。
各桁ごとに見れば良いが $60$ 桁なので桁のループは大したことがない。
https://atcoder.jp/contests/abc269/editorial/4844

y

ABC237-D

これっぽいことを再帰でやってTLEした。別に再帰でやる必要なかったので再帰をやめたら通った。
多分再帰でも参照渡しにすれば通る気がする。
解説：https://atcoder.jp/contests/abc237/editorial/3323
AC：https://atcoder.jp/contests/abc237/submissions/56716075

解説AC。なんで後ろから操作するとそうなるんだ？
解説：https://atcoder.jp/contests/abc237/editorial/3319
AC：https://atcoder.jp/contests/abc237/submissions/56715937

優先度みたいに考えればいい？値の大きい方が後に優先的に入る
- ... 2 3 ... (R)
- ... 2 4 3 ... (L)
- ... 2 4 5 3 ...(R)
L,Rはその前の数にしか影響していないから？（nとn-1の関係を表しているだけ）

y

 ABC367-Dhttps://atcoder.jp/contests/abc367/tasks/abc367_d

 TODO解いたのでまとめる．

y

 ABC275-Chttps://atcoder.jp/contests/abc275/tasks/abc275_c
ポーンの座標を全て配列に入れて4つ選んで正方形か調べた。
長さ4のvector<pair<ll,ll>>をもらって正方形か返すプログラムをGPTに書かせてしまった。

typedef pair<ll, ll> Point;

ll distanceSquared(const Point &p1, const Point &p2) {
    return (p1.first - p2.first) * (p1.first - p2.first) +
           (p1.second - p2.second) * (p1.second - p2.second);
}

bool check(vector<Point> &points) {
    if (points.size() != 4) return false;

    // 全ての距離を計算する
    vector<ll> distances;
    for (int i = 0; i < 4; i++) {
        for (int j = i + 1; j < 4; j++) {
            distances.push_back(distanceSquared(points[i], points[j]));
        }
    }

    // 距離を昇順にソート
    sort(distances.begin(), distances.end());

    // 2つの対角線の距離が等しいかつ、4つの隣接する辺の距離が等しいことを確認
    return (distances[0] == distances[1] &&  // 辺の長さ1
            distances[1] == distances[2] &&  // 辺の長さ2
            distances[2] == distances[3] &&  // 辺の長さ3
            distances[4] == distances[5] &&  // 対角線の長さが等しい
            distances[0] > 0); // 辺の長さが正の値であることを確認
}
https://atcoder.jp/contests/abc275/submissions/56919696