読書記録: Juliaによる数理最適化
https://www.coronasha.co.jp/np/isbn/9784339029345/ を読んでいく。
- 本書の方針 (まえがき参照)
- 理論の詳細を理解してアルゴリズムを実装するのではない
- JuliaやJuMP.jlなどの既存の資源は大いに使っていく方針
- 私の方針
- JuMP.jlの良い評判は聞いていたが、ほぼ未経験なので使ってみたい
- 数理最適化の色々な問題の定式化に触れたい
- 詳細に立ち入るのはなるべく避けて早く通読したい
- Zennでの技術書読書記録を試してみたい
1章
1.1 Juliaのインストール
少し古い導入方法の紹介。juliaupの紹介があった方が良かったが、書籍上の最新バージョンがv1.8.0なので執筆当時にjuliaupが普及していなかったのかも知れない。
1.2 Juliaでのパッケージ管理
Pkg.jlの紹介。本書での主な使用パッケージとして以下があるらしい。
- JuMP.jl
- CSV.jl
- DataFrames.jl
- Plots.jl
- Graphs.jl
1.3 モデラーとソルバー
モデルの書き方の紹介とソルバーの紹介など
2章
2.1 ベクトル
知ってる内容。
2.2 行列
知ってる内容。(2)
2.3 線形演算
知ってる内容。(3)
2.4 反復処理
for, while, 内包表記の紹介
3章
3.1 変数と定数
- ベクトルを太字
x -
f -
\bm{x} -
S
3.2 目的関数
- 最大化も最小化も扱う
3.3 制約条件
- 実行可能領域
S - 等式制約:
h_i(\bm{x})=0 - 不等式制約
g_j(\bm{x})\le0
- 等式制約:
3.4 数理最適化問題の分類
- 凸最適化と非凸最適化
- 凸集合の定義
- エピグラフ
\operatorname{epi}(f) = \set{(t,\bm{x}) | t \ge f(\bm{x})} - エピグラフによる凸関数の定義
- 目的関数
f S
- 線形最適化問題
-
f h_i g_j
-
- 2次最適化問題
-
f \bm{x} h_i g_j
-
- 整数最適化問題
- 線形最適化問題のうち、整数の制約が入ったもの
- 歴史的経緯から、整数最適化問題は線形に限られていた
- 最近はアルゴリズムとか計算機が発達して非線形の整数最適化も扱えるらしい
- 半正定値最適化問題
- 変数がベクトルでなく行列
- いくつかの制約により、線形最適化問題と同じ議論ができるらしい
- コメント: 具体例が思いつかないが、あとで出てくるのだろう
4章
4.1 問題例: 栄養素の問題
- 複数種類の食品に対して栄養素と価格の一覧がある
- 以下の問題は(整数)線形最適化問題になる
- 特定の栄養基準を満たす上で値段を最小化
- 特定の予算を満たす上で栄養を最大化
- コメント: 昔授業でやったときは「単に線形で、実行可能領域の頂点に解があるだけ。何が面白いんだろう」と思っていた。今はJuliaで計算できる嬉しさがモチベーションに繋がるのはある。非線形最適化問題を知ってから線形最適化問題を見ると、線形の場合にのみ適用可能な議論が見えてきて面白いのもある。
4.2 変数と定数
ベクトルの記法の流儀の説明
4.3 目的関数
- 内積
\bm{c}\cdot\bm{x} - 内積と考えても良いが、縦ベクトルと思って
\bm{c}^{\top}\bm{x} - 最大化・最小化は符号を変えればOK
- コメント:
\bm{x} \bm{c}
4.4 制約条件
複数の制約条件をまとめて行列表記することもあるらしい。
が行列
として表せる。ベクトルどうしの比較にall(A*x .≤ b)になる。
4.5 定式化
これまでの節のまとめ
4.6 解法
単体法
- 実行可能領域をなす(超)多面体の頂点を辿っていく方法
- 制約条件の増加に伴って頂点数が増えるので何らかのアルゴリズムが色々頑張ってくれるらしい
内点法
- 実行可能領域のを通ることで境界の複雑性を避ける方法
- いろいろな方法があるが、主双対内点法と呼ばれるものがよく使われるらしい
- 半正定値最適化問題にも使える方法で嬉しいらしい
プログラムを用いた求解
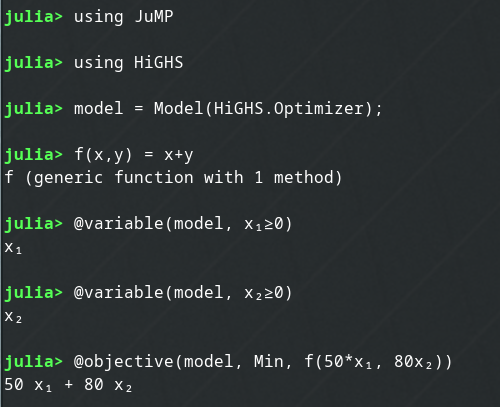
最初のJuliaコード!
using JuMP
using HiGHS
model = Model(HiGHS.Optimizer);
@variable(model, x₁≥0)
@variable(model, x₂≥0)
@objective(model, Min, 50x₁+80x₂)
@constraint(model, c1, 3x₁≥6)
@constraint(model, c2, 2x₁+4x₂≥10)
@constraint(model, c3, 2x₁+5x₂≥8)
model
print(model)
optimize!(model)
@show termination_status(model)
@show objective_value(model)
@show value(x₁), value(x₂)
vscodeでもREPLでも実行を確認。良いですね。
以下コメント
- 本書にはHiGHSやJuMPのバージョンが記載されていない。(見落としているだけ?)
- 破壊的変更(や機能追加)を見越して、バージョン記載があると良かった。
- あるいはソースコードと共にProject.tomlも配布されていると良かった。
- 数式を1つずつ入力して制約条件を入れる形式(
@constraint)- forとかで繰り返し制約条件を入れるときに不便そう
- 良い方法は用意されているはずとは思う
-
@variable(model, x₁≥0)だけでx₁がVariableRef型として定義される - その値が
value(x₁)として参照できる(最適化した後は) - マクロは自由度高くて良いですね
- 一方で、
50x₁+80x₂の代わりにユーザー定義関数は使えるのか怪しい - と思ったら使えた。sugoi
最適化には双対単体法と呼ばれるアルゴリズムが使われているらしい
forとかで繰り返し制約条件を入れるときに不便そう
良い方法は用意されているはずとは思う
と書いてましてが、すぐに回収されてましたね。
行列表記がサポートされてるのでOK
model = Model(HiGHS.Optimizer);
@variable(model, x[1:2] .≥ 0)
A = [3 0;2 4;2 5]
b = [6,10,8]
c = [50,80]
@objective(model, Min, c'*x)
@constraint(model, (A*x) .≥ b)
print(model)
optimize!(model)
@show termination_status(model)
@show objective_value(model)
@show value.(x)
ところで教科書にはtypoがあって、p47のコード15行目でx1, x2を参照しているが正しくは@show value.(x)である。
@variableでの宣言は
- 1-basedでなくても
- 行列であっても
- 三角行列でも
OK
julia> model = Model(HiGHS.Optimizer)
A JuMP Model
Feasibility problem with:
Variables: 0
Model mode: AUTOMATIC
CachingOptimizer state: EMPTY_OPTIMIZER
Solver name: HiGHS
julia> @variable(model, x[i in 1:3, j in i:3])
JuMP.Containers.SparseAxisArray{VariableRef, 2, Tuple{Int64, Int64}} with 6 entries:
[1, 1] = x[1,1]
[1, 2] = x[1,2]
[1, 3] = x[1,3]
[2, 2] = x[2,2]
[2, 3] = x[2,3]
[3, 3] = x[3,3]
実行可能領域
model = Model(HiGHS.Optimizer);
@variable(model, x[1:2] .≥ 0)
@objective(model, Max, x[1])
@constraint(model, x .≤ -10)
optimize!(model)
@show termination_status(model)
@show objective_value(model)
@show value.(x)
目的関数が定数のときはエラーでなく、x=[0.0, 0.0]を返す
model = Model(HiGHS.Optimizer);
@variable(model, x[1:2] .≥ 0)
@objective(model, Max, 0)
@constraint(model, x .≤ 10)
optimize!(model)
@show termination_status(model)
@show objective_value(model)
@show value.(x)
不等式制約は>は許容しない
model = Model(HiGHS.Optimizer);
@variable(model, x[1:2] .> 0)
- 本書にはHiGHSやJuMPのバージョンが記載されていない。(見落としているだけ?)
- 破壊的変更(や機能追加)を見越して、バージョン記載があると良かった。
- あるいはソースコードと共にProject.tomlも配布されていると良かった。
と書いたのだから、私の環境について書くべきだったな
(2023-12-26_julia-optimization) pkg> st JuMP HiGHS
Status `~/Git/julia-training/2023-12-26_julia-optimization/Project.toml`
[87dc4568] HiGHS v1.7.5
[4076af6c] JuMP v1.17.0
線形最適化問題をたくさんつくるときにinfeasible(実行可能領域が
4.7 双対問題
具体的な線形最適化問題を変形して、別の線形最適化問題を作る話。
この新しい線形最適化問題は双対問題と呼ばれる。
- 具体例だけで一般性が無いので、双対問題の定義が分からない
- 双対問題の双対問題が元の問題に戻るのか謎
- 双対問題を考えるご利益が謎
- 幾何的なイメージが謎
別の書籍ちょっと読むか
制約条件の
余ベクトルとしての等高線として解釈していい感じに理解できないかな…。
しっかり学ぶ数理最適化も眺めてみたがすぐには理解できなかった。
- 後で戻ってきて考える
- 単純な具体例を自分で作ってみる
4.8 潜在価格
未定義語の潜在価格が出てくる。シャドウ・プライスとレンジの解説が理解の助けになりそう。
あるいはJuMP.jlのドキュメントか。
追加のtypoがあり、プログラム4-7の4行目以降で不要なスペースが>と=の間に入っている。
using JuMP
using HiGHS
model = Model(HiGHS.Optimizer)
@variable(model, x₁ ≥ 0)
@variable(model, x₂ ≥ 0)
@variable(model, x₃ ≥ 0)
@objective(model, Max, 3x₁+5x₂+4x₃)
@constraint(model, c1, 2x₁+x₂+3x₃ ≤ 6)
@constraint(model, c2, 3x₁-2x₂+x₃ ≤ 7)
@constraint(model, c3, x₂+2x₃ ≤ 5)
set_silent(model)
optimize!(model)
@show termination_status(model)
@show objective_value(model)
@show shadow_price(c1)
@show shadow_price(c2)
@show shadow_price(c3)
@show value(x₁), value(x₂), value(x₃)
不等式右辺の定数の増減が目的関数の値に影響する係数をshadow_priceで出力してくれるらしい。
あくまで右辺定数のみで、
自動微分っぽい感じ(?)
4.9 輸送最適化問題
- 倉庫全体集合
I - 工場全体集合
J - 倉庫
i \in I j \in J c_{ij} - 変数: 倉庫
i j x_{ij} - 倉庫
i s_i - 工場
j d_j
とする。これが
- 最小化
\sum_{ij}c_{ij}x_{ij} - 等式制約
\sum_{i}x_{ij} = d_j - 不等式制約
\sum_{j}x_{ij} \le s_i
として線形最適化問題になる。
これをJuMP.jlで解いてみる例。
単なる数式ではなく、DictとかTupleとかDataFrameも組み合わせれる紹介もあった。
ところで、「倉庫/工場」ではなく「卸し/小売店」の方が例として適切でイメージしやすい気がする。同じ機能の工場や倉庫が独立に存在しているケースは無さそうなので。
これで4章おわり
5章 グラフ最適化問題
コメント: グラフを最適化するのか、グラフを固定した上で経路等を最適化するのか、どっちだろうか
5.1 グラフの表現
- 頂点集合
V=\set{1,2,3,4,5} E={(1,2),(2,3),(2,4),(3,4),(4,5)} - 有向グラフと無向グラフ
- Graphs.jlの紹介
最初のGraphs.jlの例
using Graphs
G = DiGraph(5)
add_edge!(G,1,2)
add_edge!(G,2,3)
add_edge!(G,2,4)
add_edge!(G,3,4)
add_edge!(G,4,5)
nv(G)
ne(G)
outneighbors(G,2)
Graphs.jlのグラフの可視化にGraphPlot.jlが良さそうだったが、あまりメンテされてない雰囲気
GraphMakie.jlで描画
using GLMakie
using GraphMakie
using Graphs
G = DiGraph(5)
add_edge!(G,1,2)
add_edge!(G,2,3)
add_edge!(G,2,4)
add_edge!(G,3,4)
add_edge!(G,4,5)
nv(G)
ne(G)
outneighbors(G,2)
graphplot(G)

5.2 最短路問題
各エッジ(枝というらしい)に重み(2点間距離)が与えられた有向グラフ上で、始点終点を結ぶパスのうち最短のものを求める問題
以下のように整数最適化問題として定式化できるらしい
記号の定義
-
n -
V=\set{1,\dots,n} -
G\in M(n,n) - 頂点
i j - 一方通行や非対称も扱える
- なので距離というと少し不正確
- 0はエッジが無いことを表す
- 頂点
-
\bm{x} - 値はbinary
-
s -
t
目的関数
-
f(\bm{x}) = \sum_{i,j} x_{ij}G_{ij}
制約条件
-
\sum_{j\ne i} x_{ij} - \sum_{k\ne i} x_{ki} = 0 - 特定の頂点
i (\ne s, t) - 一つの頂点に2個以上の枝が入ることはありえなく正確に扱えないが、定式化しやすいのでこのようにしている(?)
- 特定の頂点
-
\sum_{j\ne s} x_{sj} - \sum_{k\ne s} x_{ks} = 1 -
\sum_{j\ne s} x_{sj} = 1 \sum_{k\ne s} x_{ks} = 0 - 実行可能領域が広い方が探索しやすかったりする…?
-
-
\sum_{j\ne t} x_{tj} - \sum_{k\ne t} x_{kt} = -1 -
G_{ij}=0 \Rightarrow x_{ij}=0
微妙なtypo: 教科書のプログラム5-2の14行目でのLinearAlgebra.は不要
それ以外にも色々動かない箇所があったり自然じゃない書き方があったりする。以下のようにして実行。
using JuMP
using HiGHS
using LinearAlgebra
n = 5
V = 1:n
s = 1
t = 2
G = [
0 100 30 0 0
0 0 20 0 0
0 0 0 10 60
0 15 0 0 50
0 0 0 0 0
]
model = Model(HiGHS.Optimizer)
@variable(model, x[V, V], Bin)
@objective(model, Min, dot(G,x))
@constraint(model, [x[i,j] for i in V, j in V if G[i,j]==0] .== 0)
@constraint(model, [sum(x[i,j] for j in V if j≠i) - sum(x[j,i] for j in V if j≠i) for i in V if i ∉ (s,t)] .== 0)
@constraint(model, sum(x[s,j] for j in V if j≠s) - sum(x[j,s] for j in V if j≠s) .== 1)
@constraint(model, sum(x[t,j] for j in V if j≠t) - sum(x[j,t] for j in V if j≠t) .== -1)
set_silent(model)
optimize!(model)
@show termination_status(model)
@show objective_value(model)
for i in 1:n, j in 1:n
v = value(x[i,j])
if v ≠ 0
println("x[$i,$j] = ", v)
end
end
なんとかして整数最適化問題に落とし込めたらあとはソルバーが頑張ってくれるのでOKって感じ。
SparseArrays.jlを使って計算コスト下げる例も紹介されてる。
p89, outedgesとinedgesは空集合になりうるのでsumでなくreduceを用いているとあるが、sumでもinitが使えるのでreduceは不要だろう。(typo?)
グラフを行列(::Matrix)ではなくちゃんとグラフ(::AbstractGraph)として扱いたい
SimpleWeightedDiGraphはGraphs.jlに入っておらず、SimpleWeightedGraphs.jlが必要になる様子。
プログラム5-4でもtypo。26行目のinがnになってるっぽい。(PlutoでもJupyterでも良いので、書籍の原稿に自動変換する仕組みは無かったのかな)
プログラム5-4にまだtypo残ってたな。29,30行目以降graphs_spがspになってる
正誤表に誤りあるのウケるな…w

2 ×1ではなく2x1です。掛け算を省略できるJuliaの仕様が見難い気がするので2x₁と書く方が良い。
修正後のコード
using SimpleWeightedGraphs
using JuMP
using HiGHS
n = 5
s = 1
t = 2
V = 1:n
g = SimpleWeightedDiGraph(n)
I = [ 1, 1, 2, 3, 3, 4, 4]
J = [ 2, 3, 3, 4, 5, 2, 5]
W = [100, 30, 20, 10, 60, 15, 50]
for (i,j,w) in zip(I,J,W)
add_edge!(g,i,j,w)
end
model = Model(HiGHS.Optimizer)
@variable(model, x[i in 1:n, j in 1:n; has_edge(g, (i,j))], Bin)
@objective(model, Min, sum(v * x[i,j] for (i,j,v) in zip(I,J,W)))
@constraint(model, c_src, sum(x[s,i] for i in outneighbors(g, s)) == 1);
@constraint(model, c_dst, sum(x[i,t] for i in inneighbors(g, t)) == 1);
@constraint(model, c_flow[v in V; v≠s&&v≠t], sum(x[v,i] for i in outneighbors(g,v)) == sum(x[j,v] for j in inneighbors(g,v)))
set_silent(model)
optimize!(model)
@show termination_status(model)
@show objective_value(model)
for x in x
if value(x) == 1
println(x)
end
end
ダイクストラ法で解くのが効率的らしい
julia> using Graphs, SimpleWeightedGraphs
julia> n = 5
5
julia> s = 1
1
julia> t = 2
2
julia> V = 1:n
1:5
julia> g = SimpleWeightedDiGraph(n)
{5, 0} directed simple Int64 graph with Float64 weights
julia> I = [ 1, 1, 2, 3, 3, 4, 4]
7-element Vector{Int64}:
1
1
2
3
3
4
4
julia> J = [ 2, 3, 3, 4, 5, 2, 5]
7-element Vector{Int64}:
2
3
3
4
5
2
5
julia> W = [100, 30, 20, 10, 60, 15, 50]
7-element Vector{Int64}:
100
30
20
10
60
15
50
julia> for (i,j,w) in zip(I,J,W)
add_edge!(g,i,j,w)
end
julia> r = dijkstra_shortest_paths(g, [1], weights(g))
Graphs.DijkstraState{Float64, Int64}([0, 4, 1, 3, 3], [0.0, 55.0, 30.0, 40.0, 90.0], [Int64[], Int64[], Int64[], Int64[], Int64[]], [1.0, 1.0, 1.0, 1.0, 2.0], Int64[])
julia> r.dists
5-element Vector{Float64}:
0.0
55.0
30.0
40.0
90.0
julia> r.parents
5-element Vector{Int64}:
0
4
1
3
3
julia> dsts = [2,3,4,5]
4-element Vector{Int64}:
2
3
4
5
julia> spaths = enumerate_paths(r, dsts)
4-element Vector{Vector{Int64}}:
[1, 3, 4, 2]
[1, 3]
[1, 3, 4]
[1, 3, 5]
julia> for (i,s) in enumerate(dsts)
println("1 から $s への最短路: $(spaths[i])")
end
1 から 2 への最短路: [1, 3, 4, 2]
1 から 3 への最短路: [1, 3]
1 から 4 への最短路: [1, 3, 4]
1 から 5 への最短路: [1, 3, 5]
5.3 最大流問題
前節と同様に重み付き有向グラフに対して問題設定がなされる。
開始地点から終了地点までの流量を最大化できる(分岐を含む)経路と最大流を求める問題。重みが2頂点間の最大流量を表す。
枝や頂点上に与えられた数値を可視化するようなライブラリが欲しいな。単にSimpleWeightedDiGraphをgraphplotするだけでは数値は表示されなかった。
枝や頂点上に与えられた数値を可視化するようなライブラリが欲しいな。
GraphRecipes.jlが良さそう
教科書の図5.4をGraphRecipes.jlで試してみる。
using Graphs
using SimpleWeightedGraphs
using GraphRecipes
using Plots
using Random
n = 6
g = SimpleWeightedDiGraph(n)
I = [ 1, 1, 2, 3, 3, 4, 4, 5, 5]
J = [ 2, 3, 5, 2, 4, 5, 6, 3, 6]
W = [ 9, 6, 8, 4, 11, 6, 4, 7, 15]
for (i,j,w) in zip(I,J,W)
add_edge!(g,i,j,w)
end
edgelabel_dict = Dict()
for i in 1:n, j in 1:n
if has_edge(g,i,j)
# edgelabel_dict[(i, j)] = g.weights[j,i]
edgelabel_dict[(i, j)] = get_weight(g,i,j)
end
end
Random.seed!(42)
GraphRecipes.graphplot(g, names=1:n, edgelabel=edgelabel_dict, curves=false, nodeshape=:rect)
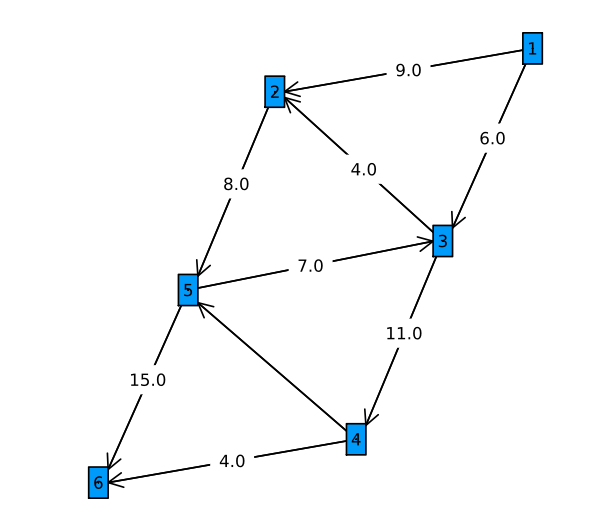
さて定式化。
記号の定義
-
n -
V -
x_{ij} i j -
w_{ij} i j -
s -
t
目的関数
\sum_{j in V} x_{sj}
制約条件
-
\sum_{j\in V} x_{ij}=\sum_{j\in V} x_{ji} 0 \le x_{ij} \le w_{ij}
教科書見ずとも実装できるようになってきた。
using JuMP
using HiGHS
s = 1
t = 2
V = 1:n
model = Model(HiGHS.Optimizer)
@variable(model, x[i in 1:n, j in 1:n; has_edge(g, (i,j))] .≥ 0)
@objective(model, Max, sum([x[s,i] for i in outneighbors(g,s)]))
@constraint(model, c_flow[v in V; v≠s&&v≠t], sum(x[v,i] for i in outneighbors(g,v)) == sum(x[j,v] for j in inneighbors(g,v)))
@constraint(model, c_max[v1 in V, v2 in V; has_edge(g,v1,v2)], x[v1,v2] ≤ get_weight(g,v1,v2))
set_silent(model)
optimize!(model)
@show termination_status(model)
@show objective_value(model)
for x in x
println(x, value(x))
end
あるいは離散より連続の方が簡単だったのかも知れない
教科書ではGraphsFlows.maximum_flowも紹介されていた。
4th引数に各枝の容量を指定する必要があるようだが、SimpleWeightedGraphs.SimpleWeightedDiGraphはサポートされていない様子。contributionチャンス!
julia> maximum_flow(g, 1, 2, g.weights')
(13.0, sparse([2, 3, 1, 3, 1, 2, 4, 5, 3, 5, 3, 4, 6, 5], [1, 1, 2, 2, 3, 3, 3, 3, 4, 4, 5, 5, 5, 6], [-9.0, -4.0, 9.0, 4.0, 4.0, -4.0, -2.0, 2.0, 2.0, -2.0, -2.0, 2.0, 0.0, 0.0], 6, 6))
julia> maximum_flow(g, 1, 2)
(2, sparse([2, 3, 1, 3, 1, 2], [1, 1, 2, 2, 3, 3], [-1, -1, 1, 1, 1, -1], 6, 6))
これで5章までおわり
一旦5章までの内容の正誤連絡を送った。