Juliaで二項係数を計算する!(Base.binomialの実装解説)
イントロ
二項係数
が成り立つので、これをJuliaで計算するには
function my_binomial(n,k)
if n == k == 0
1
elseif n == 0
0
else
my_binomial(n-1,k) + my_binomial(n-1,k-1)
end
end
として関数my_binomialを定義すればよいでしょう。
Juliaには元からbinomialが備わっているので、それを使って検算ができます。
julia> my_binomial(12,4)
495
julia> binomial(12,4)
495
合ってますね。これらの違いは何でしょうか?
BenchmarkTools.jlで確認してみましょう。
julia> using BenchmarkTools
julia> @benchmark my_binomial(12,4)
BenchmarkTools.Trial: 10000 samples with 1 evaluation.
Range (min … max): 12.291 μs … 38.621 μs ┊ GC (min … max): 0.00% … 0.00%
Time (median): 13.410 μs ┊ GC (median): 0.00%
Time (mean ± σ): 13.527 μs ± 587.929 ns ┊ GC (mean ± σ): 0.00% ± 0.00%
▄▆ █
▂▁▂▁▂▁▁▁▂▂▂▂▂▁▂▂▁▄▆▆███▁█▄▁▆▇▅▅▆▄▁▂▂▁▂▂▂▂▂▂▁▂▂▁▂▂▂▂▂▂▁▂▂▁▂▂▂ ▃
12.3 μs Histogram: frequency by time 15.2 μs <
Memory estimate: 0 bytes, allocs estimate: 0.
julia> @benchmark binomial(12,4)
BenchmarkTools.Trial: 10000 samples with 998 evaluations.
Range (min … max): 12.176 ns … 23.933 ns ┊ GC (min … max): 0.00% … 0.00%
Time (median): 13.506 ns ┊ GC (median): 0.00%
Time (mean ± σ): 13.585 ns ± 0.541 ns ┊ GC (mean ± σ): 0.00% ± 0.00%
▄▄ ▅█ ▂
▂▂▂▁▂▂▂▁▂▂▂▁▂▂▂▁▂▂▃▁▅██▁██▄▁▆██▁▇▅▃▁▂▂▂▁▂▂▂▁▂▂▂▁▂▂▂▁▂▂▂▁▂▂▂ ▃
12.2 ns Histogram: frequency by time 15.3 ns <
Memory estimate: 0 bytes, allocs estimate: 0.
どちらも同じくらい…と思いきや 13.527 μs と 13.585 ns なので1000倍の速度差があることが確認できます。
本記事ではbinomialの実装を通じて
- 高速なコードの書き方
- オーバーフローに対応した書き方
- 汎用的(様々な型に対応可能)な書き方
について解説していきます。
実行環境
本記事では以下の環境で実行しています。
julia> versioninfo()
Julia Version 1.7.3
Commit 742b9abb4d (2022-05-06 12:58 UTC)
Platform Info:
OS: Linux (x86_64-pc-linux-gnu)
CPU: AMD Ryzen 7 4700U with Radeon Graphics
WORD_SIZE: 64
LIBM: libopenlibm
LLVM: libLLVM-12.0.1 (ORCJIT, znver2)
Baseでの実装の確認
Juliaの@lessマクロを使えばBase.binomialがどのような実装になっているか確認できます。
julia> @less binomial(12,4)
表示結果は以下のとおりです。
function binomial(n::T, k::T) where T<:Integer
n0, k0 = n, k
k < 0 && return zero(T)
sgn = one(T)
if n < 0
n = -n + k -1
if isodd(k)
sgn = -sgn
end
end
k > n && return zero(T)
(k == 0 || k == n) && return sgn
k == 1 && return sgn*n
if k > (n>>1)
k = (n - k)
end
x::T = nn = n - k + 1
nn += 1
rr = 2
while rr <= k
xt = div(widemul(x, nn), rr)
x = xt % T
x == xt || throw(OverflowError("binomial($n0, $k0) overflows"))
rr += 1
nn += 1
end
convert(T, copysign(x, sgn))
end
GitHubのリポジトリでは以下が該当するスクリプトになります。
実装の解説
高速化のための漸化式
冒頭では
の漸化式を使っていました。
この漸化式はPascalの三角形を手で計算するときには便利ですが、与えられた
代わりに
の漸化式を使うと便利です。[1]
function my_binomial2(n,k)
if k == 0
1
elseif k == n
1
elseif 1 ≤ k ≤ n-1
my_binomial2(n-1,k-1)*n/k
else
0
end
end
検算とベンチマークです。
julia> my_binomial2(12,4)
495.0
julia> @benchmark my_binomial2(12,4)
BenchmarkTools.Trial: 10000 samples with 998 evaluations.
Range (min … max): 17.985 ns … 32.471 ns ┊ GC (min … max): 0.00% … 0.00%
Time (median): 19.524 ns ┊ GC (median): 0.00%
Time (mean ± σ): 19.542 ns ± 0.732 ns ┊ GC (mean ± σ): 0.00% ± 0.00%
▁ ▅█▅▇
▂▂▂▂▂▂▂▂▂▂▂▂▂▃▄▆█▇▆▄████▆▄▃▃▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▁▂▂▂▂ ▃
18 ns Histogram: frequency by time 22.2 ns <
Memory estimate: 0 bytes, allocs estimate: 0.
-
my_binomial2はmy_binomialに比べてかなり高速になりました!まだbinomialには遠いですね。 -
my_binomial2(12,4)は値として正しいですが浮動小数点数の495.0になっています。
型安定な除算
整数同士の/は浮動小数点数を返します。今回は除算の結果が整数になることが分かっているので、divを使ったほうが良いです。
function my_binomial3(n,k)
k == 0 && return 1
k == n && return 1
1 ≤ k ≤ n-1 && return div(my_binomial3(n-1,k-1)*n, k)
return 0
end
Juliaでは論理和(|, ||)と論理積(&,&&)が用意されています。
1文字の|,&は関数ですが、2文字の||,&&は制御句なのでif...endの代わりに使うことができます。
高速化には寄与しませんが、Baseの実装に合わせるためにifの代わりに使っています。
julia> @benchmark my_binomial3(12,4)
BenchmarkTools.Trial: 10000 samples with 998 evaluations.
Range (min … max): 15.605 ns … 29.181 ns ┊ GC (min … max): 0.00% … 0.00%
Time (median): 17.145 ns ┊ GC (median): 0.00%
Time (mean ± σ): 17.119 ns ± 0.726 ns ┊ GC (mean ± σ): 0.00% ± 0.00%
▂ ██▆▆
▂▂▂▂▂▂▂▂▃▁▃▃▃▂▂▃▆▇█▁█▆▆████▆▄▁▃▃▃▂▂▂▂▂▂▁▂▂▂▂▂▂▂▂▂▁▂▂▂▂▂▂▂▂▂ ▃
15.6 ns Histogram: frequency by time 19.3 ns <
Memory estimate: 0 bytes, allocs estimate: 0.
僅かに高速化されました!( 19.542 ns → 17.119 ns )
Base実装での 13.585 ns にはまだ足りないので、他の箇所でまだまだ改善できそうですね。
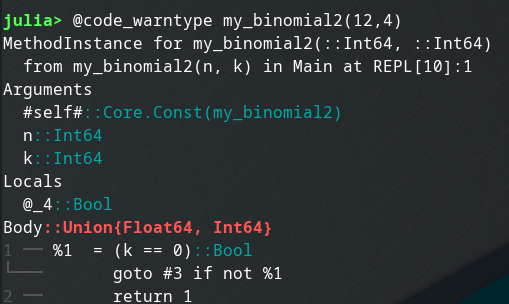
ちなみに、型不安定性は@code_warntypeマクロで確認できます。
julia> @code_warntype my_binomial2(12,4)
MethodInstance for my_binomial2(::Int64, ::Int64)
from my_binomial2(n, k) in Main at REPL[10]:1
Arguments
#self#::Core.Const(my_binomial2)
n::Int64
k::Int64
Locals
@_4::Bool
Body::Union{Float64, Int64}
1 ── %1 = (k == 0)::Bool
└─── goto #3 if not %1
2 ── return 1
3 ── %4 = (k == n)::Bool
└─── goto #5 if not %4
4 ── return 1
5 ── %7 = (1 ≤ k)::Bool
└─── goto #7 if not %7
6 ── %9 = (n - 1)::Int64
│ (@_4 = k ≤ %9)
└─── goto #8
7 ── (@_4 = false)
8 ┄─ goto #10 if not @_4
9 ── %14 = (n - 1)::Int64
│ %15 = (k - 1)::Int64
│ %16 = Main.my_binomial2(%14, %15)::Union{Float64, Int64}
│ %17 = (%16 * n)::Union{Float64, Int64}
│ %18 = (%17 / k)::Float64
└─── return %18
10 ─ return 0
julia> @code_warntype my_binomial3(12,4)
MethodInstance for my_binomial3(::Int64, ::Int64)
from my_binomial3(n, k) in Main at REPL[13]:1
Arguments
#self#::Core.Const(my_binomial3)
n::Int64
k::Int64
Locals
@_4::Bool
Body::Int64
1 ── %1 = (k == 0)::Bool
└─── goto #3 if not %1
2 ── return 1
3 ── %4 = (k == n)::Bool
└─── goto #5 if not %4
4 ── return 1
5 ── %7 = (1 ≤ k)::Bool
└─── goto #7 if not %7
6 ── %9 = (n - 1)::Int64
│ (@_4 = k ≤ %9)
└─── goto #8
7 ── (@_4 = false)
8 ┄─ goto #10 if not @_4
9 ── %14 = (n - 1)::Int64
│ %15 = (k - 1)::Int64
│ %16 = Main.my_binomial3(%14, %15)::Int64
│ %17 = (%16 * n)::Int64
│ %18 = Main.div(%17, k)::Int64
└─── return %18
10 ─ return 0
少し長いですが、my_binomial2(12,4)のBody::Union{Float64, Int64}が型不安定を表しています。
zennに実行結果を貼り付けているだけなので分かりにくいですが、REPLで実行すれば型不安定な箇所を赤文字で表示してくれます。
再帰呼び出しを避ける
function my_binomial4(n,k)
k == 0 && return 1
k == n && return 1
1 ≤ k ≤ n-1 || return 0
x = 1
for _k in 1:k
_n = n - k + _k
x = div(x*_n, _k)
end
return x
end
julia> my_binomial4(12,4)
495
julia> @benchmark my_binomial4(12,4)
BenchmarkTools.Trial: 10000 samples with 1000 evaluations.
Range (min … max): 0.978 ns … 16.552 ns ┊ GC (min … max): 0.00% … 0.00%
Time (median): 2.375 ns ┊ GC (median): 0.00%
Time (mean ± σ): 2.386 ns ± 0.409 ns ┊ GC (mean ± σ): 0.00% ± 0.00%
█
▂▁▁▁▁▁▁▁▁▁▁▁▂▁▁▂▁▁▁▁▁▁▁▁▁▂▁▃▁▁▃▁▁▁▁▁▁▁▂▁▅▁█▁▁▇▁▁▁▁▁▁▁▂▁▃▁▃ ▂
0.978 ns Histogram: frequency by time 2.86 ns <
Memory estimate: 0 bytes, allocs estimate: 0.
17.119 ns → 2.386 ns になって大幅に高速化できました!
Base.binomialが 13ns 程度だったので、Juliaの実装よりも高速になってしまいましたね…。
そういう訳で、高速な実装が欲しければBaseの関数を自分で再実装することも時には有用です。
オーバーフロー対策
二項係数は以下のように書くことができます。
階乗を使っているため、オーバーフローは容易に起こると予想できますね。
発散のオーダーはStirlingの公式などで確認できますが、ここでは数値実験で確かめましょう。
julia> binomial(0,0)
1
julia> binomial(20,10)
184756
julia> binomial(40,20)
137846528820
julia> binomial(60,30)
118264581564861424
julia> binomial(80,40)
ERROR: OverflowError: binomial(80, 40) overflows
Stacktrace:
[1] binomial(n::Int64, k::Int64)
@ Base ./intfuncs.jl:1042
[2] top-level scope
@ REPL[63]:1
ちゃんとエラーを吐いてくれますね。
しかしmy_binomial4ではエラーを出力せずに負の値を返します。
julia> my_binomial4(80,40)
-15097783517027730
オーバーフローを避けて正しい値が欲しい場合は以下のようにBigIntを使えばOKです。
julia> my_binomial4(BigInt(80),BigInt(40))
107507208733336176461620
julia> binomial(BigInt(80),BigInt(40))
107507208733336176461620
オーバーフローを検知するために以下のようにmy_binomial5を定義します。
function my_binomial5(n,k)
k == 0 && return 1
k == n && return 1
1 ≤ k ≤ n-1 || return 0
x = 1
for _k in 1:k
_n = n - k + _k
_x = div(widemul(x,_n), _k) # 型を拡張して計算
x = _x % Int # 元の型に収める
x == _x || throw(OverflowError("overflow"))
end
return x
end
ここで
-
widemul(x,_n)-
widemulは掛け算 - ただしオーバーフローしない型を選んで計算する
- 例えば
widemul(::UInt8,::UInt8)::UInt16,widemul(::Int64,::Int64)::UInt128などです。
-
-
x % Int-
%は余りの計算で、例えば128 % 5は3です - 第2引数には整数型を入れることもできて、例えば
1729 % Int8は-63です
-
検算とベンチマークをしましょう!
julia> my_binomial5(12,4)
495
julia> my_binomial5(80,40)
ERROR: OverflowError: overflow
Stacktrace:
[1] my_binomial5(n::Int64, k::Int64)
@ Main ./REPL[65]:10
[2] top-level scope
@ REPL[67]:1
julia> @benchmark my_binomial5(12,4)
BenchmarkTools.Trial: 10000 samples with 998 evaluations.
Range (min … max): 15.745 ns … 31.072 ns ┊ GC (min … max): 0.00% … 0.00%
Time (median): 17.145 ns ┊ GC (median): 0.00%
Time (mean ± σ): 17.168 ns ± 0.632 ns ┊ GC (mean ± σ): 0.00% ± 0.00%
█ █▅▆
▂▂▂▂▁▂▂▁▂▂▂▂▂▂▁▄▆█▇▆▆█▁███▆▄▃▁▂▂▂▂▂▂▁▂▂▂▂▂▂▂▁▂▂▂▂▂▂▁▂▂▂▂▂▂▂ ▃
15.7 ns Histogram: frequency by time 19.3 ns <
Memory estimate: 0 bytes, allocs estimate: 0.
何故かbinomial(12,4)の13nsよりも遅くなっちゃいましたね。
初期値変更で高速化
先にネタバレすると、1回x == _x || throw(OverflowError("overflow"))を実行するたびに 4ns 程度掛かっています。
my_binomial5(12,4)の計算では「my_binomial5(11,4) → my_binomial5(10,3) → my_binomial5(9,2) → my_binomial5(8,1) → my_binomial5(7,0) == 0」の4回で合計 16ns くらい掛かります。
なので、これを使えば少し高速化できそうです。つまりmy_binomial5(12,4)のケースでは my_binomial5(8,1) == 8 は自明なのでオーバーフローチェックの回数を1回減らせそうです。
function my_binomial6(n,k)
k == 0 && return 1
k == n && return 1
1 ≤ k ≤ n-1 || return 0
x = n - k + 1 # 初期値を1から変更
for _k in 2:k # _kの範囲を2からに変更
_n = n - k + _k
_x = div(widemul(x,_n), _k)
x = _x % Int
x == _x || throw(OverflowError("overflow"))
end
return x
end
これで確認しましょう。
julia> my_binomial6(12,4)
495
julia> my_binomial6(80,40)
ERROR: OverflowError: overflow
Stacktrace:
[1] my_binomial6(n::Int64, k::Int64)
@ Main ./REPL[69]:10
[2] top-level scope
@ REPL[71]:1
julia> @benchmark my_binomial6(12,4)
BenchmarkTools.Trial: 10000 samples with 999 evaluations.
Range (min … max): 11.954 ns … 46.631 ns ┊ GC (min … max): 0.00% … 0.00%
Time (median): 13.423 ns ┊ GC (median): 0.00%
Time (mean ± σ): 13.768 ns ± 1.861 ns ┊ GC (mean ± σ): 0.00% ± 0.00%
▁▃ ▃▄▅█▇▆▅ ▁ ▁ ▂
▆████████████▆▇█▇█▇▄▁▁▁▁▄▁▁▃▃▃▃▅▁▄▄▄▃▄▁▃▄▃▃▁▃▃▅▆▆▄▇▆▆▇▅▆▆██ █
12 ns Histogram: log(frequency) by time 23.1 ns <
Memory estimate: 0 bytes, allocs estimate: 0.
Baseのbinomial(12,4)と同程度の速度になりました!
対称性を使った高速化
以下はどちらも同じ値ですが
julia> my_binomial6(12,4)
495
julia> my_binomial6(12,8)
495
ベンチマークを取ると後者の方が遅いです。
julia> @benchmark my_binomial6(12,8)
BenchmarkTools.Trial: 10000 samples with 995 evaluations.
Range (min … max): 22.111 ns … 61.348 ns ┊ GC (min … max): 0.00% … 0.00%
Time (median): 29.691 ns ┊ GC (median): 0.00%
Time (mean ± σ): 29.938 ns ± 1.732 ns ┊ GC (mean ± σ): 0.00% ± 0.00%
▃▂▅▅█▅▄▁ ▁ ▁ ▁
▃▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▆█████████▆█▇█▇█▆██▇▅▁▄▃▄▁▁▆▅▇▃▆▅▆▆▆▆ █
22.1 ns Histogram: log(frequency) by time 37.9 ns <
Memory estimate: 0 bytes, allocs estimate: 0.
よって、kを選ぶようにすれば高速化ができそうです。
function my_binomial7(n,k)
k == 0 && return 1
k == n && return 1
1 ≤ k ≤ n-1 || return 0
if div(n,2) < k
k = n - k # kが大きければn-kに置き換え
end
x = n - k + 1
for _k in 2:k
_n = n - k + _k
_x = div(widemul(x,_n), _k)
x = _x % Int
x == _x || throw(OverflowError("overflow"))
end
return x
end
ベンチマークとりましょう!
julia> my_binomial7(12,4)
495
julia> my_binomial7(12,8)
495
julia> @benchmark my_binomial7(12,4)
BenchmarkTools.Trial: 10000 samples with 999 evaluations.
Range (min … max): 11.885 ns … 53.481 ns ┊ GC (min … max): 0.00% … 0.00%
Time (median): 13.492 ns ┊ GC (median): 0.00%
Time (mean ± σ): 13.595 ns ± 0.718 ns ┊ GC (mean ± σ): 0.00% ± 0.00%
▄▄▆█ ▁▃
▂▁▁▁▂▁▂▂▂▂▂▁▂▂▂▂▂▁▂▂▂▄▅▁████▅▁▇███▆▁▄▂▂▂▂▁▂▂▂▂▂▁▂▂▂▂▂▁▂▂▂▂▂ ▃
11.9 ns Histogram: frequency by time 15.3 ns <
Memory estimate: 0 bytes, allocs estimate: 0.
julia> @benchmark my_binomial7(12,8)
BenchmarkTools.Trial: 10000 samples with 999 evaluations.
Range (min … max): 11.884 ns … 152.683 ns ┊ GC (min … max): 0.00% … 0.00%
Time (median): 13.492 ns ┊ GC (median): 0.00%
Time (mean ± σ): 13.704 ns ± 3.768 ns ┊ GC (mean ± σ): 0.00% ± 0.00%
▅▆█ ▁▃
▂▂▂▂▂▁▂▃▃▃▃▁▂▂▂▃▃▁▃▃▃▄▆▇████▆▃▅███▆▂▄▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂▂ ▃
11.9 ns Histogram: frequency by time 15.4 ns <
Memory estimate: 0 bytes, allocs estimate: 0.
my_binomial7(12,4)の速度を落とさずにmy_binomial7(12,8)の高速化ができました!
複数の整数型への対応
Int32の入力に対してはInt32を返してほしいですが、現状のmy_binomial7ではそのようになっていません。
julia> my_binomial7(Int32(12),Int32(4)) |> typeof
Int64
julia> binomial(Int32(12),Int32(4)) |> typeof
Int32
これを解決するには以下のようにすればOKです。
function my_binomial8(n::T, k::T) where T<:Integer
k == 0 && return one(T) # one(T)は型Tの乗法単位元を返す関数
k == n && return one(T)
1 ≤ k ≤ n-1 || return zero(T) # zero(T)は型Tの加法単位元を返す関数
if div(n,2) < k
k = n - k
end
x = n - k + one(T)
for _k in 2:k
_n = n - k + _k
_x = div(widemul(x,_n), _k)
x = _x % T
x == _x || throw(OverflowError("overflow"))
end
return x
end
戻り値の型も期待通りで、引数の型に応じてオーバーフローも正しく検知できていますね。
julia> my_binomial8(Int32(12), Int32(4))
495
julia> my_binomial8(Int32(12), Int32(4)) |> typeof
Int32
julia> my_binomial8(Int8(12),Int8(4))
ERROR: OverflowError: overflow
Stacktrace:
[1] my_binomial8(n::Int8, k::Int8)
@ Main ./REPL[23]:13
[2] top-level scope
@ REPL[30]:1
n
julia> binomial(-1,3)
-1
julia> binomial(-2,3)
-4
まだmy_binomial8は対応できていないですね。
julia> my_binomial8(-1,3)
0
julia> my_binomial8(-2,3)
0
以下の等式を満たす係数を二項係数と定義すれば、
例えば、
のMaclaurin展開によって二項係数を計算できます。[2]
Base.binomialでは以下のように正しく計算ができていることが確認できます。
julia> binomial.(-1,0:5)
6-element Vector{Int64}:
1
-1
1
-1
1
-1
ここではこれ以上立ち入りませんが、Baseでの定義では以下のコードの周辺が該当する箇所になります。
Baseの実装との差異
これまでの解説で、ほぼBaseの実装を再現することができました。
まだ違いが残っていますが、あとは細かい部分です。
-
Base実装のrrはmy_binomial8の_kに相当 -
Base実装のnnはmy_binomial8の_nに相当 -
Baseではforの代わりにwhileを使っている -
Baseではdiv(n,2)の代わりにビットシフト演算n>>1を使っている
オーバーフローの扱い
他の関数でのオーバーフローの例
前述のように、オーバーフローのチェックによってBase.binomialは速度低下を引き起こしているようでした。
しかし、他の関数ではオーバーフローが確認されないことの方も多いです。
julia> Int8(100) + Int8(10)
110
julia> Int8(100) + Int8(100)
-56
julia> typemax(Int)
9223372036854775807
julia> typemax(Int)+1
-9223372036854775808
julia> typemax(Int)
9223372036854775807
julia> typemax(Int)*2
-2
julia> binomial(10,5)
252
julia> binomial(100,50)
ERROR: OverflowError: binomial(100, 50) overflows
Stacktrace:
[1] binomial(n::Int64, k::Int64)
@ Base ./intfuncs.jl:1042
[2] top-level scope
@ REPL[12]:1
julia> 2^10
1024
julia> 2^100
0
julia> factorial(10)
3628800
julia> factorial(100)
ERROR: OverflowError: 100 is too large to look up in the table; consider using `factorial(big(100))` instead
Stacktrace:
[1] factorial_lookup
@ ./combinatorics.jl:19 [inlined]
[2] factorial(n::Int64)
@ Base ./combinatorics.jl:27
[3] top-level scope
@ REPL[18]:1
julia> abs(Int8(-127))
127
julia> abs(Int8(-128))
-128
この実行結果から、以下のような方針でオーバーフローのチェックが入っていることと推測されます:
- 計算時間を抑えるため、指数関数以下のオーダーの関数に対してはオーバーフローをチェックしない
- 指数関数より大きいオーダーの関数(e.g.
factorial,binomial)は、引数が小さくてもオーバーフローしがちなので丁寧にエラーを出す
オーバーフローチェック周辺の高速化について
二項係数は正規分布を使って近似することができる[3]ため、これを使えばBase.binomialのオーバーフローのチェック回数を減らして大幅に高速化できるかも知れません。
階乗については、計算結果をVectorとして内部的に保持しているのでbinomialのような高速化は難しいようです:
julia> Base._fact_table64
20-element Vector{Int64}:
1
2
6
24
120
720
5040
40320
362880
3628800
39916800
479001600
6227020800
87178291200
1307674368000
20922789888000
355687428096000
6402373705728000
121645100408832000
2432902008176640000
SaferIntegers.jlを使ったオーバーフロー回避
掛け算などの通常の演算でも、整数型のオーバーフローを避けたい方も居るかも知れません。
その場合はSaferIntegers.jlパッケージを使えばOKです!
julia> using SaferIntegers
julia> SafeInt8(127)
127
julia> SafeInt8(-128)
-128
julia> abs(SafeInt8(-128))
ERROR: OverflowError: cannot take `abs(typemin)`
Stacktrace:
[1] abs(x::SafeInt8)
@ SaferIntegers ~/.julia/packages/SaferIntegers/WCXig/src/int_ops.jl:32
[2] top-level scope
@ REPL[9]:1
julia> SafeInt8(-128) - 3
ERROR: OverflowError: -128 - 3 overflowed for type Int8
Stacktrace:
[1] throw_overflowerr_binaryop(op::Symbol, x::Int8, y::Int8)
@ Base.Checked ./checked.jl:154
[2] checked_sub
@ ./checked.jl:223 [inlined]
[3] -
@ ~/.julia/packages/SaferIntegers/WCXig/src/arith_ops.jl:35 [inlined]
[4] -(x::SafeInt8, y::Int64)
@ SaferIntegers ~/.julia/packages/SaferIntegers/WCXig/src/arith_ops.jl:75
[5] top-level scope
@ REPL[10]:1
まとめ
- Juliaの
Base.binomialの実装をほぼ再現できました。 - エラー処理を諦めれば、
Base.binomialをより高速化できることが確認できました。 - Juliaのオーバーフローの扱いについて例示しました。
-
この式についてはtsujimotterさんの解説の二項係数を求める関数の作り方 (Ruby編)を参照してください。 ↩︎
-
n \ge 0 \sum_{k}\binom{n}{k} = 2^n 1-1+1-1+\cdots 1/2 n=-1 \sum_{k}\binom{n}{k} = 2^n -
詳しくは二項分布の正規近似(ラプラスの定理)を参照してください ↩︎
Discussion