🏳️‍🌈

紙を編んで曲面を作ろう！ (ElasticSurfaceEmbedding.jlの紹介)

2022/11/30に公開

Julia

本記事はJuliaLang Advent Calendar 2022の1日目の記事です!
Julia好きの方々の多くは数学が好きで、数学が好きな方々は曲面が好きだと思います！！
本記事はそのような方々に向けて書きました！！！

はじめに

先月、はじめての論文をarXivで公開しました！
紙を編んで曲面をつくる研究で、理論的な解説は連ツイにあります。

製作中の様子↓

本記事では、この理論をJuliaで実装したElasticSurfaceEmbedding.jlの解説^[1]をします！

パッケージのインストール

Juliaのpkgモードで以下を実行してください。

(@v1.8) pkg> add BasicBSpline StaticArrays IntervalSets
(@v1.8) pkg> add https://github.com/hyrodium/BasicBSplineExporter.jl
(@v1.8) pkg> add https://github.com/hyrodium/ElasticSurfaceEmbedding.jl

最初の実行例: 放物面

この曲面は以下の画像のようにして作っています。

左から順に:

曲面の形状の定義
曲面を長細い曲面片に分割
それぞれの曲面片の切り出し形状の計算
平面材料(紙)から切り出し
編んで完成！

この一連の流れにおいて 3.の「切り出し形状の計算」 が一番非自明で、この計算をするパッケージがElasticSurfaceEmbedding.jlです。あとでもう少し詳しく説明しますが、この形状は「歪エネルギー^[2]を最小にする2次元Euclid空間への埋め込み」として特徴づけられています。"ElasticSurfaceEmbedding"の名前にはこの意味が込められています。

放物面を編むための切り出し形状を計算するには以下を実行します。(REPLにコピペすればOK)

using IntervalSets
using BasicBSpline
using StaticArrays
using ElasticSurfaceEmbedding
ElasticSurfaceEmbedding.𝒑₍₀₎(u¹,u²) = SVector(u¹, u², u¹^2+u²^2)
n = 10
D(i,n) = (-1.0..1.0, (i-1)/n..i/n)
allsteps = AllSteps()
for i in 1:10
    initial_state!(allsteps, D(i,n), n₁=25)
    newton_onestep!(allsteps, fixingmethod=:fix3points)
    newton_onestep!(allsteps)
    refinement!(allsteps, p₊=(0,1), k₊=(EmptyKnotVector(),KnotVector([(i-1/2)/10])))
    newton_onestep!(allsteps)
    newton_onestep!(allsteps)
    pin!(allsteps)
end
export_pinned_steps(".", allsteps, unitlength=(50, "mm"), mesh=(20,1), xlims=(-2,2), ylims=(-1,1))

処理内容の解説は後述するとして、実行結果はallstepsの出力から確認できます。

`allsteps`の出力

julia> allsteps
1: Initial state - domain: [-1.0, 1.0]×[0.0, 0.1]
└─2: Newton onestep - residual norm: 3.0098e-02, Δa norm: 1.9847e-02, computation time: 22ms
  └─3: Newton onestep - residual norm: 1.8804e-03, Δa norm: 1.3264e-02, computation time: 22ms
    └─4: Refinement - p₊:(0, 1), k₊:(Bool[], [0.05])
      └─5: Newton onestep - residual norm: 1.8434e-03, Δa norm: 4.3219e-03, computation time: 77ms
        └─6: 📌 Newton onestep - residual norm: 2.7186e-06, Δa norm: 1.3806e-04, computation time: 99ms
7: Initial state - domain: [-1.0, 1.0]×[0.1, 0.2]
└─8: Newton onestep - residual norm: 3.3025e-02, Δa norm: 2.3630e-02, computation time: 31ms
  └─9: Newton onestep - residual norm: 1.9982e-03, Δa norm: 1.4734e-02, computation time: 25ms
    └─10: Refinement - p₊:(0, 1), k₊:(Bool[], [0.15])
      └─11: Newton onestep - residual norm: 1.6288e-03, Δa norm: 1.0403e-02, computation time: 81ms
        └─12: 📌 Newton onestep - residual norm: 3.9412e-06, Δa norm: 3.1503e-04, computation time: 82ms
13: Initial state - domain: [-1.0, 1.0]×[0.2, 0.3]
└─14: Newton onestep - residual norm: 3.6870e-02, Δa norm: 2.6618e-02, computation time: 24ms
  └─15: Newton onestep - residual norm: 2.1813e-03, Δa norm: 1.3912e-02, computation time: 24ms
    └─16: Refinement - p₊:(0, 1), k₊:(Bool[], [0.25])
      └─17: Newton onestep - residual norm: 1.3023e-03, Δa norm: 1.2485e-02, computation time: 83ms
        └─18: 📌 Newton onestep - residual norm: 4.4132e-06, Δa norm: 3.3974e-04, computation time: 82ms
19: Initial state - domain: [-1.0, 1.0]×[0.3, 0.4]
└─20: Newton onestep - residual norm: 4.0001e-02, Δa norm: 2.8676e-02, computation time: 24ms
  └─21: Newton onestep - residual norm: 2.3386e-03, Δa norm: 1.2158e-02, computation time: 23ms
    └─22: Refinement - p₊:(0, 1), k₊:(Bool[], [0.35])
      └─23: Newton onestep - residual norm: 9.7245e-04, Δa norm: 1.2222e-02, computation time: 83ms
        └─24: 📌 Newton onestep - residual norm: 3.9234e-06, Δa norm: 2.7297e-04, computation time: 83ms
25: Initial state - domain: [-1.0, 1.0]×[0.4, 0.5]
└─26: Newton onestep - residual norm: 4.1891e-02, Δa norm: 3.0282e-02, computation time: 23ms
  └─27: Newton onestep - residual norm: 2.4125e-03, Δa norm: 1.0475e-02, computation time: 23ms
    └─28: Refinement - p₊:(0, 1), k₊:(Bool[], [0.45])
      └─29: Newton onestep - residual norm: 6.9762e-04, Δa norm: 1.0958e-02, computation time: 83ms
        └─30: 📌 Newton onestep - residual norm: 3.1803e-06, Δa norm: 1.8120e-04, computation time: 82ms
31: Initial state - domain: [-1.0, 1.0]×[0.5, 0.6]
└─32: Newton onestep - residual norm: 4.2636e-02, Δa norm: 3.1610e-02, computation time: 24ms
  └─33: Newton onestep - residual norm: 2.4006e-03, Δa norm: 9.0638e-03, computation time: 23ms
    └─34: Refinement - p₊:(0, 1), k₊:(Bool[], [0.55])
      └─35: Newton onestep - residual norm: 4.9253e-04, Δa norm: 9.3891e-03, computation time: 81ms
        └─36: 📌 Newton onestep - residual norm: 2.4826e-06, Δa norm: 1.0638e-04, computation time: 82ms
37: Initial state - domain: [-1.0, 1.0]×[0.6, 0.7]
└─38: Newton onestep - residual norm: 4.2520e-02, Δa norm: 3.2710e-02, computation time: 23ms
  └─39: Newton onestep - residual norm: 2.3252e-03, Δa norm: 7.9393e-03, computation time: 23ms
    └─40: Refinement - p₊:(0, 1), k₊:(Bool[], [0.65])
      └─41: Newton onestep - residual norm: 3.5192e-04, Δa norm: 7.8423e-03, computation time: 85ms
        └─42: 📌 Newton onestep - residual norm: 1.8940e-06, Δa norm: 5.9199e-05, computation time: 83ms
43: Initial state - domain: [-1.0, 1.0]×[0.7, 0.8]
└─44: Newton onestep - residual norm: 4.1818e-02, Δa norm: 3.3595e-02, computation time: 24ms
  └─45: Newton onestep - residual norm: 2.2113e-03, Δa norm: 7.0824e-03, computation time: 24ms
    └─46: Refinement - p₊:(0, 1), k₊:(Bool[], [0.75])
      └─47: Newton onestep - residual norm: 2.6462e-04, Δa norm: 6.4460e-03, computation time: 84ms
        └─48: 📌 Newton onestep - residual norm: 1.4061e-06, Δa norm: 3.3403e-05, computation time: 87ms
49: Initial state - domain: [-1.0, 1.0]×[0.8, 0.9]
└─50: Newton onestep - residual norm: 4.0747e-02, Δa norm: 3.4278e-02, computation time: 23ms
  └─51: Newton onestep - residual norm: 2.0776e-03, Δa norm: 6.4475e-03, computation time: 23ms
    └─52: Refinement - p₊:(0, 1), k₊:(Bool[], [0.85])
      └─53: Newton onestep - residual norm: 2.1727e-04, Δa norm: 5.2313e-03, computation time: 83ms
        └─54: 📌 Newton onestep - residual norm: 1.0064e-06, Δa norm: 1.9814e-05, computation time: 83ms
55: Initial state - domain: [-1.0, 1.0]×[0.9, 1.0]
└─56: Newton onestep - residual norm: 3.9462e-02, Δa norm: 3.4782e-02, computation time: 24ms
  └─57: Newton onestep - residual norm: 1.9369e-03, Δa norm: 5.9769e-03, computation time: 23ms
    └─58: Refinement - p₊:(0, 1), k₊:(Bool[], [0.95])
      └─59: Newton onestep - residual norm: 1.9491e-04, Δa norm: 4.1940e-03, computation time: 84ms
        └─60: 📌 Newton onestep - residual norm: 6.8995e-07, Δa norm: 1.2158e-05, computation time: 83ms

実行結果は./pinned以下にSVG画像として出力されます。

.
└── pinned
    ├── pinned-6.svg
    ├── pinned-12.svg
    ├── pinned-18.svg
    ├── pinned-24.svg
    ├── pinned-30.svg
    ├── pinned-36.svg
    ├── pinned-42.svg
    ├── pinned-48.svg
    ├── pinned-54.svg
    └── pinned-60.svg

全画像をそのまま貼り付けると長くなるのでpinned-6.svgの例:

SVGファイルで出力された全ての形状を合わせるとは以下^[3]のようになります。

この形状をレーザー加工機^[4]で切り出し、編み上げれば放物面が完成します！イエイ！

コードの解説

前節では天下り的にコードを提示していました。本節はその解説です。

パッケージ読み込み

using IntervalSets
using BasicBSpline
using StaticArrays
using ElasticSurfaceEmbedding

まずはパッケージの読み込みですね。
BasicBSpline.jlは以前の記事でも紹介したパッケージですが、元々は本研究のために書いたコードがベースになっています。

曲面形状の定義

ElasticSurfaceEmbedding.𝒑₍₀₎(u¹,u²) = SVector(u¹, u², u¹^2+u²^2)

は曲面の形状を定義です。少し気持ち悪いですが、メソッドの上書きによって形状を定義しています。^[5]

n = 10
D(i,n) = (-1.0..1.0, (i-1)/n..i/n)

こちらは分割された曲面片の定義域の定義ですね。

数値計算

allsteps = AllSteps()

計算結果を木構造で持つためのインスタンスを定義します。

for i in 1:10
    initial_state!(allsteps, D(i,n), n₁=25)
    newton_onestep!(allsteps, fixingmethod=:fix3points)
    newton_onestep!(allsteps)
    refinement!(allsteps, p₊=(0,1), k₊=(EmptyKnotVector(),KnotVector([(i-1/2)/10])))
    newton_onestep!(allsteps)
    newton_onestep!(allsteps)
    pin!(allsteps)
end

ここがメインの処理で、以下のステップを繰り返す処理になります。

初期値決定(initial_state!)
- iを回して定義域を $[-1,1]\times[0.0,0.1]$ から $[-1,1]\times[0.9,1.0]$ まで計算。
- 測地的曲率をもとに初期形状を決定する。
Newton法(newton_onestep!)
- Newton法で計算しているので収束は早い。
  収束の自動判定は未実装(数回決め打ちで十分)。
Refinement(refinement!)
- 制御点を増やして数値解の精度向上を図る方法。

SVG出力するステップをpin!(allsteps)で指定しています。

SVG画像出力

export_pinned_stepsを実行すればpin!(allsteps)で指定されたステップがSVG画像として出力されます。
第1引数は出力パスで、キーワード引数はそれぞれ以下の意味です。

unitlength=(50, "mm"): SVG画像における1の長さ
mesh=(20,1): 曲面片に貼るメッシュの数(正確には四角の数)
xlims=(-2,2): SVG画像の横方向の範囲
ylims=(-1,1): SVG画像の縦方向の範囲

すこし発展的な解説

理論の詳細は論文や連ツイを読んでいただきたいですが、本節では数値計算に関わりそうな部分を簡単に紹介したいと思います。

歪エネルギー最小化

平面材料を変形させて曲面片をつくるとき、以下の図のように材料内に引張と圧縮が発生します。この変形に係るエネルギーが歪エネルギーであり、これを最小化するような切り出し形状が最適な形状だと定義します。

ただし、材料の変形としては「平面形状を曲面片に変形」(下図左)よりも「曲面片を平面形状に変形」(下図右)の方が直観的に扱いやすいです。

引張と圧縮の位置こそ入れ替わりますが、歪エネルギーはほぼ同じ^[6]なので変形の向きを入れ替えても問題ありません。

B-spline多様体

歪エネルギー最小化の問題は弱形式の偏微分方程式として与えられます。Galerkin法で解くので通常のFEMのように3角形メッシュで解いても良かったのですが、ElasticSurfaceEmbedding.jlではB-splineを使っています。以下がその理由です：

滑らかな形状を表現できる
定義域が矩形なのでB-spline多様体と相性が良い

B-splineの詳しい資料は以下を参照してください！

B-spline入門（線形代数がすこし分かる人向け）
- 音声付きで学びたい人はこちら。
- 数理的なモチベーションが伝わりやすい…はず
NURBS多様体による形状表現
- 証明を詳細にフォローしたい人はこちら。
- PDF資料
BasicBSpline.jlのドキュメント
- Juliaで実行しながらB-splineを勉強したい人はこちら。
- 英語で書いてます。
BasicBSpline.jlを作ったので宣伝です！
- Juliaで実行しながらB-splineを勉強したい人はこちら。
- 日本語ですが、古い情報が多くなってきたので書き直す予定。

途中の計算結果

前述のexport_pinned_steps関数では、ピン留めしたステップのみSVGとして出力することができました。
export_all_steps関数を使えば、ピン留めしていないすべてのステップについて歪のプロットまで表示することが可能になります。

export_all_steps(".",allsteps, mesh=(20,1), xlims=(-2,2), ylims=(-1,1))

例えばi=9の曲面片(定義域が $[-1, 1]\times[0.8, 0.9]$ のもの)に対しては以下のように、歪が徐々に緩和されていく様子が見て取れます。

./combined/combined-49.png

./combined/combined-50.png

./combined/combined-51.png

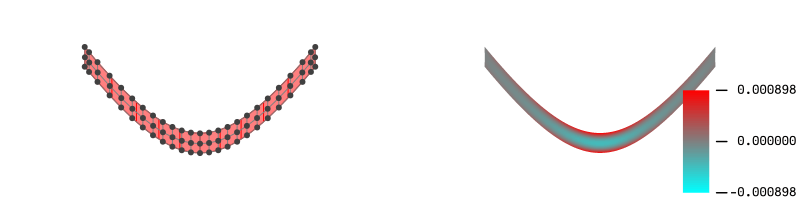
./combined/combined-52.png

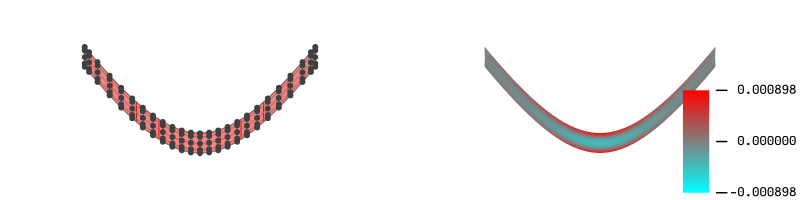
./combined/combined-53.png

./combined/combined-54.png

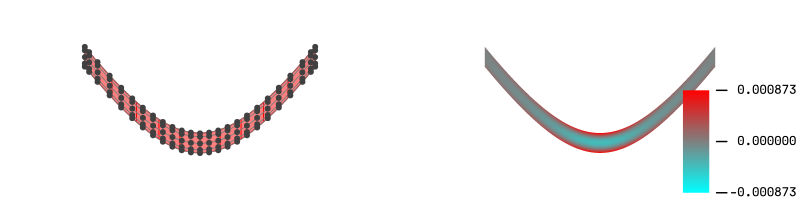
おわりに

本プロジェクトは私が修士課程に居たときから始めたもので、計算スクリプト・理論の大枠自体は4年前には完成していました。ただ、論文を書くのがとにかく大変で、OSS活動や労働などをしていたらこんなに時間が経ってしまっていました。

次の目標は

より多くの曲面模型を作ること
より多くの人に曲面模型を作る喜びを知ってもらうこと

です。本記事では2番目の目標のために書きました。JuliaTokai #13 年末LT大会2022でもこのパッケージについて話す予定です。

そういう訳で、みなさま是非にElasticSurfaceEmbedding.jlで曲面模型を作って下さい！
完成した際にはTwitterなどで報告してもらえると嬉しいです！！

脚注

Documenter.jlで作ったドキュメントは https://hyrodium.github.io/ElasticSurfaceEmbedding.jl/dev/ にあります。 ↩︎
物体の変形で発生するエネルギーのこと。通常はひずみエネルギーと書かれることが多いですが、筆者の好みで平仮名を避けています。 ↩︎
この埋め込み形状は論文のAppendix Bにも記載されています。 ↩︎
もちろん印刷してハサミで切ってもOKです！ ↩︎
引数に関数を入れるように実装したことがありましたが、実行速度の低下があったので断念しました。詳細な速度低下の原因は未調査で、今後時間があれば修正される可能性があります。ただ、複数の形状を同時に計算しないはずなので、メソッドの上書きでも大きな問題にはなりません。 ↩︎
「ほぼ」というのは「材料非線形性を無視する限りは」という意味です。 ↩︎

GitHubで編集を提案

はじめに

パッケージのインストール

最初の実行例: 放物面

コードの解説

パッケージ読み込み

曲面形状の定義

数値計算

SVG画像出力

すこし発展的な解説

歪エネルギー最小化

B-spline多様体

途中の計算結果

おわりに

Discussion