Swiftで初等関数の近似値を求める

なぜSwiftなの？

Swiftは環境構築などする必要がなく,MacかiPadがあればPlaygroundsをインストールするだけで使うことができる。
また,Playgroundsにはステップ実行やゆっくり実行という機能があり,for文やwhile分をステップごとに実行し,実行されている時の値の変化を確認することもできる。
さらに,ビューア機能を使えば変数の変化の様子を勝手にグラフ表示してくれる。

sin(x)

sinxのマクローリン展開

$sinx$をマクローリン展開すると,

$$sinx = x - \frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+⋯+\frac{(-1)^{n-1}x^{2n-1}}{(2n-1)!}+⋯$$

と表されるのであった。この記事では$sinx$の近似値をプログラミングを使って求めていく。(言語はSwift)ipadでも大丈夫。

1.変数を用意する

マクローリン展開は何回でも微分できる関数$f(x)$を$x$の冪乗関数の級数の展開式の和で近似させるものであるのであった。この記事では$sinx$の値をsumとして,sumにだんだん値を加えていく。

var sum = 0
print(sum)    //0
sum += 1
print(sum)    //1

また,近似する$x$を入れる定数も用意しなければならない。この時近似する値として$\pi/6$や$\pi/3$などの値を用いたいので,$\pi$が使えるようimport Foundationを書いておく。

import Foundation
var sum = 0
let x = Double.pi/2

さらに,項として更新され続ける変数を用意する。

var item = x

第一項は定数と同じになるので,xを入れておく。

最終的なコードは以下のようになる。

2.x=π/2として,第二項までコーディングする

コーディングをする上で小さな値から始めることや具体的な値で試行錯誤することは重要だと思う。(個人の見解)。この記事でもその理念に則り$x=\pi/2$として第二項まで,つまり

$$sinx=x-\frac{x^3}{3!}$$

までコーディングする。

import Foundation
var sum = 0.0  //int型とdouble型は足算できないので,0.0と書きdouble型にする。
var x = Double.pi/2

sum += x
sum += -(x*x*x)/Double(3*2*1)

sumに$x$を加え,次の行で$-\frac{x^3}{3!}$を加えている。

最後に真値と比較するprint文を加える。

import Foundation
var sum = 0.0  //int型とdouble型は足算できないので,0.0と書きdouble型にする。
var x = Double.pi/2

sum += x
sum += -(x*x*x)/Double(3*2*1)

print(sum)//近似値0.9248322292886504
print(sin(Double.pi/2))//真値1.0

Double(3*2*1)としているのはInt型をDoule型に変換しているのだが,この記事では本質的な部分ではないので説明は割愛。

3.一般化しやすいように工夫する

さっきは第二項を-(x*x*x)/3*2*1としたが,これでは項数が増えるたびに$x$を増やさなければならない。項数が増えても短くコーディングすることができるように工夫を加える。

import Foundation
var sum = 0.0  //int型とdouble型は足算できないので,0.0と書きdouble型にする。
var x = Double.pi/2

sum += x

for i in 2 ..< 3{
    x *= -(x*x)/Double((2*(i-1))*(2*i-1))
    sum += x
    print(x)
}

print(sum)//近似値0.9248322292886504
print(sin(Double.pi/2))//真値1.0

forを使い,項と変数iを対応させた。(1回しか実行されないが。)この場合第二項のみしか行わないので,for i in 2 ..< 3としている。一般化しているが,計算としては同じであるので2で出した答えと同じになるはずだ。

4.項数を増やす

一般化することによって項数を増やしても対応できる。

import Foundation
var sum = 0.0  //int型とdouble型は足算できないので,0.0と書きdouble型にする。
let x = Double.pi/2
var item = x

sum += item

for i in 2 ..< 6{
    item *= -(x*x)/Double((2*(i-1))*(2*i-1))
    sum += item
}

print(sum)//近似値1.00000035425842861
print(sin(Double.pi/2))//真値1.0

第6項までの近似,つまり

$$sinx= x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\frac{x^9}{9!}-\frac{x^{11}}{11!}$$

ではほとんど誤差が無いことがわかる。

cos(x)

cosxのマクローリン展開

$cosx$をマクローリン展開すると,

$$cosx=1-\frac{x^2}{2!}+\frac{x^4}{4!}-⋯+\frac{(-1)^nx^{2n}}{(2n)!}+⋯$$

と表されるのであった。この記事では$sinx$の近似値をプログラミングを使って求めていく。(言語はSwift)ipadでも大丈夫。

1.変数を用意する

マクローリン展開は何回でも微分できる関数$f(x)$を$x$の冪乗関数の級数の展開式の和で近似させるものであるのであった。この記事では$sinx$の値をsumとして,sumにだんだん値を加えていく。

var sum = 0
print(sum)    //0
sum += 1
print(sum)    //1

また,近似する$x$を入れる定数も用意しなければならない。この時近似する値として$\pi/6$や$\pi/3$などの値を用いたいので,$\pi$が使えるようimport Foundationを書いておく。

import Foundation
var sum = 0
let x = Double.pi/2

さらに,項として更新され続ける変数を用意する。

var item = x

第一項は定数と同じになるので,xを入れておく。

最終的なコードは以下のようになる。

import Foundation
var sum = 0.0  //int型とdouble型は足算できないので,0.0と書きdouble型にする。
let x = Double.pi/2
var item = x

2.x=π/2として,第二項までコーディングする

コーディングをする上で小さな値から始めることや具体的な値で試行錯誤することは重要だと思う。(個人の見解)。この記事でもその理念に則り$x=\frac{\pi}{2}$として第二項まで,つまり

$$cosx=1-\frac{x^2}{2!}$$

までコーディングする。

import Foundation
var sum = 0.0  //int型とdouble型は足算できないので,0.0と書きdouble型にする。
let x = Double.pi/2
var item = 1

sum += 1
sum += -(x*x)/Double(2*1)

sumに$1$を加え,次の行で$-\frac{x^2}{2!}$を加えている。

最後に真値と比較するprint文を加える。

import Foundation
var sum = 0.0  //int型とdouble型は足算できないので,0.0と書きdouble型にする。
var x = Double.pi/2

sum += 1
sum += -(x*x*x)/Double(3*2*1)

print(sum)//近似値0.9248322292886504
print(sin(Double.pi/2))//真値1.0

Double(2*1)としているのはInt型をDoule型に変換しているのだが,この記事では本質的な部分ではないので説明は割愛。

3.一般化しやすいように工夫する

さっきは第二項を$-\frac{x^2}{2!}$としたが,これでは項数が増えるたびに$x$を増やさなければならない。項数が増えても短くコーディングすることができるように工夫を加える。

import Foundation
var sum = 0.0  //int型とdouble型は足算できないので,0.0と書きdouble型にする。
let x = Double.pi/3
var item = 1

sum += item

for i in 1 ..< 3{
    item *= -(x*x)/Double((2*i)*(2*i-1))
    sum += item
}

print(sum)//近似値0.525479753410744
print(cos(Double.pi/3))//真値0.5

4.項数をふやす

一般化することによって項数を増やしても対応できる。

import Foundation
var sum = 0.0  //int型とdouble型は足算できないので,0.0と書きdouble型にする。
let x = Double.pi/3
var item = 1.0

sum += item

for i in 1 ..< 6{
    item *= -(x*x)/Double((2*i)*(2*i-1))
    sum += item
}

print(sum)//近似値0.499999999639
print(cos(Double.pi/3))//真値0.5

第6項までの近似,つまり

$$cosx=1-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}+\frac{x^8}{8!}-\frac{x^{10}}{10!}$$

ではほとんど誤差が無いことがわかる。

おまけ

一般化するときは表にすると捉えやすい。

log(x+1)

log(x+1)のマクローリン展開

$\log(1+x)$のマクローリン展開は

$$\log(1+x) = x-\frac{x^2}{2}+\frac{x^3}{3}-\frac{x^4}{4}+⋯+\frac{(-1)^{n-1}x^n}{n}+⋯$$

と表されるのであった。この記事では$sinx$の近似値をプログラミングを使って求めていく。(言語はSwift)ipadでも大丈夫。

1.変数を用意する

マクローリン展開は何回でも微分できる関数$f(x)$を$x$の冪乗関数の級数の展開式の和で近似させるものであるのであった。この記事では$\log x$の値をsumとして,sumにだんだん値を加えていく。

var sum = 0
print(sum)    //0
sum += 1
print(sum)    //1

また,近似する$x$を入れる定数も用意しなければならない。

var sum = 0
let x = 1

さらに,項として更新され続ける変数を用意する。

var item = x

第一項は定数と同じになるので,xを入れておく。

最終的なコードは以下のようになる。

var sum = 0.0  //int型とdouble型は足算できないので,0.0と書きdouble型にする。
let x = 1.0
var item = x

2.x=1として第二項までコーディングする

コーディングをする上で小さな値から始めることや具体的な値で試行錯誤することは重要だと思う。(個人の見解)。この記事でもその理念に則り$x=1$として第二項まで,つまり

$$\log (1+x)=x-\frac{x^2}{2}$$

までコーディングする。

var sum = 0.0  //int型とdouble型は足算できないので,0.0と書きdouble型にする。
let x = 1.0
var item = x

sum += 1.0
sum += -(x*x)/Double(2*1)

最後に真値と比較するprint文を加える。

import Foundation
var sum = 0.0  //int型とdouble型は足算できないので,0.0と書きdouble型にする。
let x = 1.0
var item = x

sum += 1.0
sum += -(x*x)/Double(2*1)
print(sum)//近似値0.5
print(log(2.0))//真値0.6931471805599453

3.一般化しやすいように工夫する

さっきは第二項を$-\frac{x^2}{2}$としたがこれでは項数が増えるたびに$x$を増やしたり分母をいじったりしなければならない。項数が増えても短くコーディングすることができるように工夫を加える。

import Foundation
var sum = 0.0  //int型とdouble型は足算できないので,0.0と書きdouble型にする。
var item = 1.0
let x = 1.0
sum += item

for i in 2 ..< 3{
    item *= -(x*Double(i-1))/Double(i)
    sum += item
}
print(sum)//近似値0.5
print(log(2.0))//真値0.6931471805599453

マクローリン展開された$\log (x+1)$を観察すると,項が大きくなるたび$x$と$1/n$がかけられているので,それをコードで表現する。

for文を使っているが,1度しか実行されないため,sumの値は変わらない。

4.項数をふやす

一般化することによって項数を増やしても対応できる。

import Foundation
var sum = 0.0  //int型とdouble型は足算できないので,0.0と書きdouble型にする。
var item = 1.0
let x = 1.0
sum += item

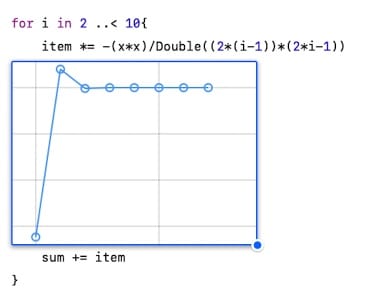
for i in 2 ..< 10{
    item *= -(x*Double(i-1))/Double(i)
    sum += item
}
print(sum)//近似値0.7456349206349205
print(log(2.0))//真値0.6931471805599453

第９項まで加えても真値とだいぶ差がある。$sinx,cosx$は第6項でほとんど同じだったので,$\log (x+1)$は$sin$や$cos$に比べ,収束するのが遅いことがわかる。