足し算に+演算子は必要ない
概要
半導体に用いられている、半加算器・全加算器の仕組みを理解する
前提知識
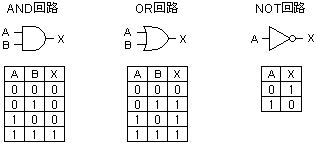
論理演算
小学校で図のような直列回路と並列回路の勉強をしましたね。

電球をそれぞれA, Bとすると、それぞれのON/OFFによって回路全体のON/OFFはどうなるでしょうか?
直列回路
直列回路の場合、それぞれの電球の状態と回路全体の状態は以下のようになりますね。
| A | B | 回路全体 |
|---|---|---|
| ○ | ○ | ○ |
| ○ | × | × |
| × | ○ | × |
| × | × | × |
これは何を表しているかと言うと、プログラミングでいうところのAND(A AND B)ですね。
つまり、直列回路とはANDの論理演算をすることができるということです。
並列回路
並列回路の場合、それぞれの電球の状態と回路全体の状態は以下のようになりますね。
| A | B | 回路全体 |
|---|---|---|
| ○ | ○ | ○ |
| ○ | × | ○ |
| × | ○ | ○ |
| × | × | × |
予想がつくと思いますが、これはプログラミングでいうところのOR(A OR B)ですね。
つまり、並列回路とはORの論理演算をすることができるということです。
筆算
皆さんは足し算するときにどうしますか?
1+1のような簡単なものなら暗算で2と答えられるかもしれません。
9869598 + 9894835はどうでしょうか?
暗算だと少し難しいので筆算を用いる人が多いかもしれません。
では2進数の足し算はどうでしょうか?
101 + 110
これくらいなら1011と暗算でも出せそうです。
1001 + 1101はどうでしょうか?
筆算を使って計算してみましょう。

見て分かる通り、同じ桁の数を足して、2になる場合は繰り上がる、というような計算になりますよね。
半加算器
実はこれ、先程紹介した直列回路と並列回路で表現できるんです。
わかりやすくするために、直列回路をANDゲート、並列回路をORゲート、値を逆にするNOTゲートを使います。
これをうまいこと組み合わせると、半加算器(half adder)というものが作れます。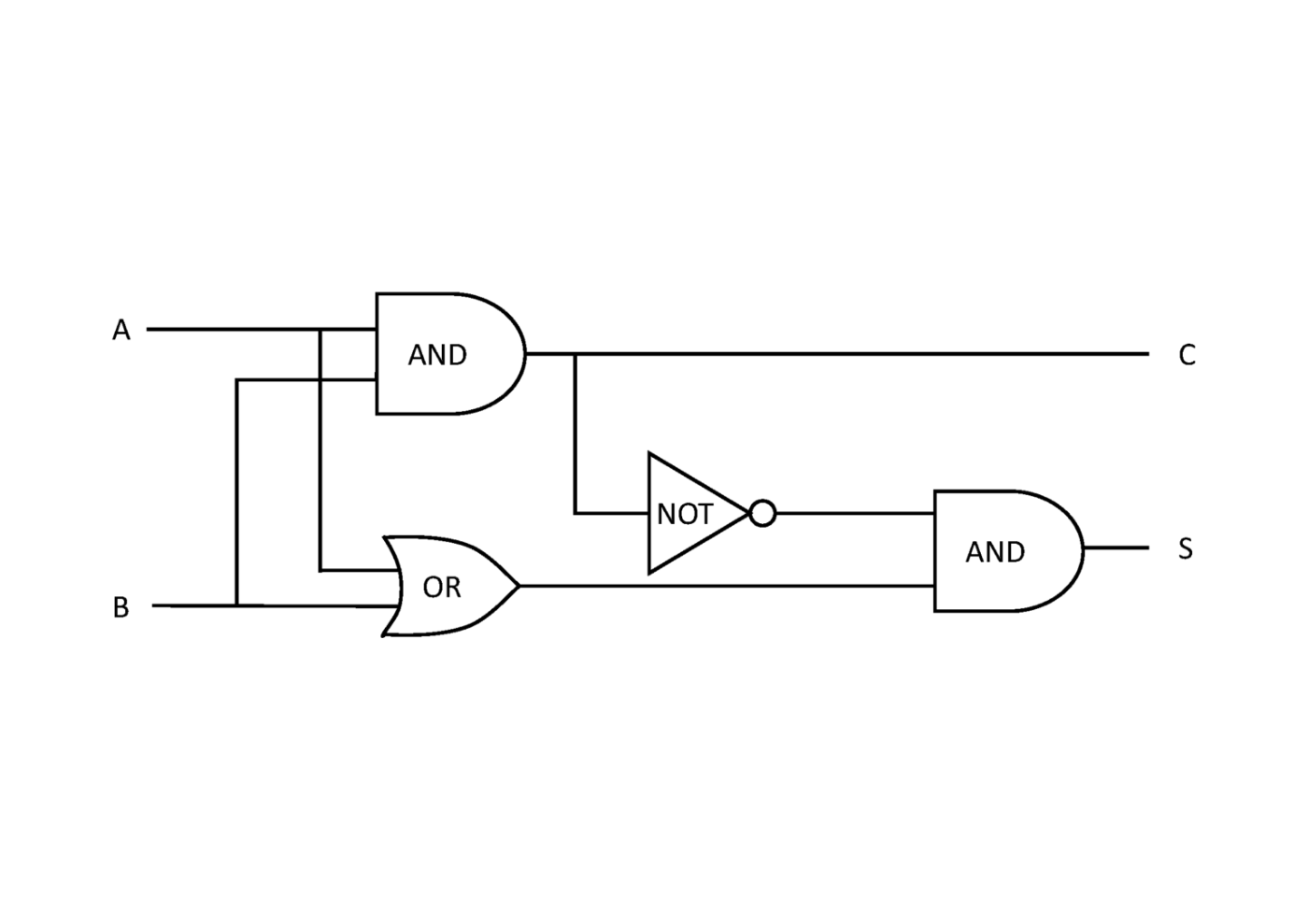
A, Bが入力で、Sはその桁の計算結果、Cは繰り上がりの値になります。
ただし、A,Bは一桁(0,1)の値しか取らないので、このままだと(A, B) = (0, 0), (1, 0), (0, 1), (1, 1)の4パターンの計算しかできません。
全加算器
さらに、半加算器に桁上りの入力を考慮できるようにしたものが全加算器(all adder)です。

各桁の値がA,Bとして、桁上りの入力がXとしてインプットされ、アウトプットとして桁の計算結果と桁上りの値を出力します。
これで一桁の計算は問題なさそうです。
そして、この全加算器を桁数分接続したものが、筆算となるわけです。
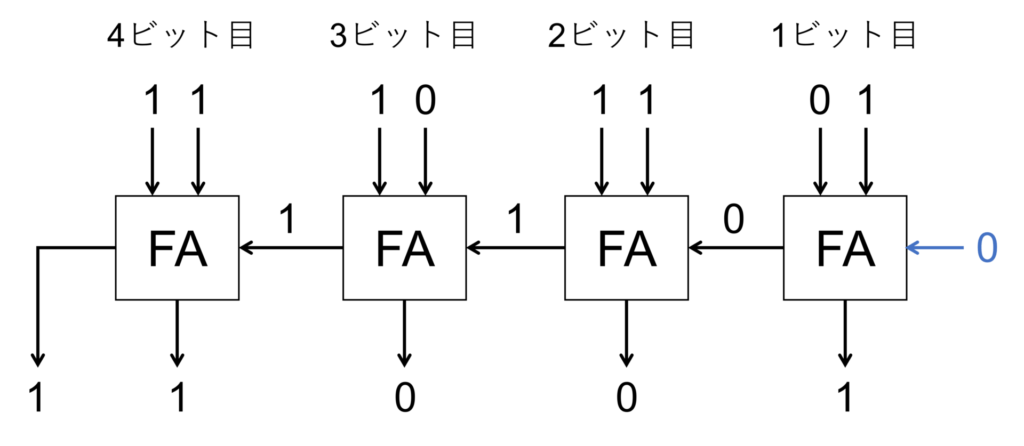
パソコンはこのようにして計算しているんですね。
実際にコードを書いて再現してみましょう
コードで再現
pythonで半加算器、全加算器を記述するとそれぞれ以下のようになります。
# 半加算器
def halfAdder(a: int , b: int):
c: int = a and b
s: int = (a or b) and not c
return {'c': c, 's': s}
# 全加算器
def fullAdder(a: int , b: int , x: int):
cs_from_ab: dict = halfAdder(a, b)
cs_from_sx: dict = halfAdder(cs_from_ab['s'], x)
c: int = cs_from_ab['c'] or cs_from_sx['c']
s: int = cs_from_sx['s']
return {'c': c, 's': s}
足し算は以下のように書けます(コード汚いですがご了承ください)
# 足し算
def add(a, b):
# 2進数に変換
bin_a: str = bin(a)[2:]
bin_b: str = bin(b)[2:]
length: int = max([len(bin_a), len(bin_b)])
# 0埋め
a: str = bin_a.zfill(length)
b: str = bin_b.zfill(length)
# 計算結果をlistに保存
results: list = []
c: int = 0
for i in range(length):
# 各桁を足し算
calc: dict = fullAdder(int(a[-1 -i]), int(b[-1 -i]), int(c))
c: int = calc['c']
results.insert(0, int(calc['s']))
if calc['c'] == 1:
results.insert(0, int(calc['c']))
# 計算結果を文字列に変換
sum = ''.join([str(result) for result in results])
# 10進数に変換
result: int = int(sum, 2)
print(a)
print(b)
print(sum)
return result
def sample():
result = add(9, 13)
print (result)
計算結果は以下です
1001
1101
10110
22
ちゃんと計算できていますね。
何桁でも大丈夫です
// result = add(234235, 532523)
00111001001011111011
10000010000000101011
10111011001100100110
766758
まとめ
何気なく使っている加算処理でも、内部ではかなり複雑なことが行われていて驚きですね。こういったハード面についてあまり勉強することがないので、なかなか面白かったです。
Discussion