【Python】回帰分析とは何か？

回帰分析は、データの中から関係性を見つけ出す統計手法です。

今回は、初心者にもわかりやすく回帰分析の基本を説明します。

回帰分析とは？

回帰分析とは、あるデータ（説明変数）から別のデータ（目的変数）を予測するための手法です。

たとえば、勉強時間から試験の点数を予測したり、広告費から売上を予測したりする時に使います。

データ間の関係を数式で表すことで、未来の予測ができるようになります。

なぜ回帰分析が役立つのか？

回帰分析を使うと、以下のようなことができるようになります：

1. データ間の関係性を理解できる
2. 将来の値を予測できる
3. どの要素が結果に大きく影響しているかを知ることができる

例えば、会社が「広告費をもっと使うべきか」と考える時に、広告費と売上の関係を回帰分析で調べることで、その判断材料にできます。

回帰分析の種類

主な回帰分析には以下のようなものがあります：

種類	説明	用途
単回帰分析	説明変数が1つの回帰分析	勉強時間と点数の関係など
重回帰分析	説明変数が複数の回帰分析	気温、湿度、天候から売上予測など
ロジスティック回帰	結果が「成功か失敗か」などの二値の場合	合格/不合格の予測など

今回はとくに単回帰分析と重回帰分析に焦点を当てていきます。

単回帰分析をPythonで実装してみよう

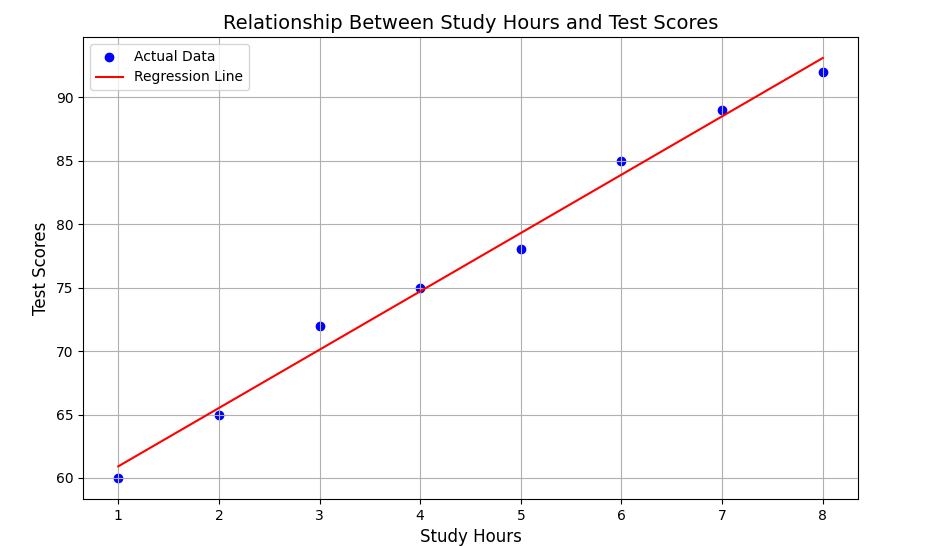
まずは、単回帰分析の例として、勉強時間と試験の点数の関係を分析してみましょう。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
import pandas as pd

# サンプルデータの作成（勉強時間と点数）
study_hours = np.array([1, 2, 3, 4, 5, 6, 7, 8]).reshape(-1, 1)
test_scores = np.array([60, 65, 72, 75, 78, 85, 89, 92])

# 回帰モデルの作成
model = LinearRegression()
model.fit(study_hours, test_scores)

# モデルの係数と切片を表示
print(f"係数: {model.coef_[0]:.2f}")
print(f"切片: {model.intercept_:.2f}")

# 予測値の計算
predicted_scores = model.predict(study_hours)

# 英語表記でのプロット
plt.figure(figsize=(10, 6))
plt.scatter(study_hours, test_scores, color='blue', label='Actual Data')
plt.plot(study_hours, predicted_scores, color='red', label='Regression Line')
plt.title('Relationship Between Study Hours and Test Scores', fontsize=14)
plt.xlabel('Study Hours', fontsize=12)
plt.ylabel('Test Scores', fontsize=12)
plt.legend()
plt.grid(True)
plt.show()

# 新しい勉強時間での予測
new_study_time = np.array([[9]])  # 9時間勉強した場合
predicted_score = model.predict(new_study_time)
print(f"9時間勉強した場合の予測点数: {predicted_score[0]:.2f}")

この例では：

1. 勉強時間と点数のサンプルデータを用意しています
2. LinearRegressionモデルで回帰分析を行っています
3. 回帰直線のグラフを表示しています
4. 新しい勉強時間（9時間）での点数を予測しています

表示されるグラフ

回帰分析の評価方法

回帰分析の結果がどれだけ良いのかを評価するための指標もあります：

from sklearn.metrics import r2_score, mean_squared_error

# 決定係数（R²）の計算
r2 = r2_score(test_scores, predicted_scores)
print(f"決定係数（R²）: {r2:.4f}")

# 平均二乗誤差（MSE）の計算
mse = mean_squared_error(test_scores, predicted_scores)
print(f"平均二乗誤差（MSE）: {mse:.4f}")

決定係数（R²）は0〜1の値をとり、1に近いほど予測精度が高いことを示します。

平均二乗誤差（MSE）は小さいほど良いモデルとされます。

重回帰分析の例

つぎに、複数の要素から予測する重回帰分析の例を見てみましょう：

import numpy as np
from sklearn.linear_model import LinearRegression
import pandas as pd
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

# サンプルデータの作成（勉強時間、睡眠時間、点数）
data = {
    'study_hours': [1, 2, 3, 4, 5, 6, 7, 8],
    'sleep_hours': [4, 5, 6, 7, 8, 6, 7, 8],
    'test_score': [62, 67, 74, 76, 82, 86, 90, 93]
}
df = pd.DataFrame(data)
print("データの確認:")
print(df.head())

# 説明変数と目的変数の設定
X = df[['study_hours', 'sleep_hours']]  # 説明変数（勉強時間と睡眠時間）
y = df['test_score']  # 目的変数（点数）

# 重回帰モデルの作成
model = LinearRegression()
model.fit(X, y)

# モデルの係数と切片を表示
print(f"勉強時間の係数: {model.coef_[0]:.2f}")
print(f"睡眠時間の係数: {model.coef_[1]:.2f}")
print(f"切片: {model.intercept_:.2f}")

# 回帰式の表示
equation = f"点数 = {model.coef_[0]:.2f} × 勉強時間 + {model.coef_[1]:.2f} × 睡眠時間 + {model.intercept_:.2f}"
print(f"回帰式: {equation}")

# 決定係数の表示
r2 = model.score(X, y)
print(f"決定係数 R²: {r2:.4f}")

# 新しいデータでの予測（DataFrame形式で特徴量名を保持）
new_data = pd.DataFrame([[9, 7]], columns=['study_hours', 'sleep_hours'])
predicted_score = model.predict(new_data)
print(f"勉強時間9時間、睡眠時間7時間の場合の予測点数: {predicted_score[0]:.2f}")

# 3Dグラフの作成
fig = plt.figure(figsize=(12, 8))
ax = fig.add_subplot(111, projection='3d')

# 実測値のプロット
ax.scatter(df['study_hours'], df['sleep_hours'], df['test_score'], 
           c='blue', marker='o', s=100, label='Actual Values')

# 予測平面のためのグリッドデータ作成
x_surf = np.linspace(1, 9, 30)
y_surf = np.linspace(4, 8, 30)
x_surf, y_surf = np.meshgrid(x_surf, y_surf)

# 予測値の計算
Z = model.intercept_ + model.coef_[0] * x_surf + model.coef_[1] * y_surf

# 予測平面のプロット
ax.plot_surface(x_surf, y_surf, Z, alpha=0.3, color='green', label='Prediction Plane')

# 新しいデータポイントのプロット
ax.scatter(new_data['study_hours'].values[0], new_data['sleep_hours'].values[0], predicted_score[0], 
           c='red', marker='*', s=200, label='Predicted Point')

# グラフの設定
ax.set_xlabel('Study Hours')
ax.set_ylabel('Sleep Hours')
ax.set_zlabel('Test Score')
ax.set_title('Multiple Regression Analysis of Test Scores Based on Study and Sleep Hours')

# 凡例の追加
ax.legend()

# グラフの表示
plt.tight_layout()
plt.show()

この例では勉強時間に加えて睡眠時間も考慮して、より複雑な関係性を分析しています。

表示されるグラフ

回帰分析の手順

実際のデータで回帰分析を行う時の一般的な手順は次のとおりです：

1. データの準備と前処理
2. データの可視化と関係性の確認
3. トレーニングデータとテストデータに分割
4. モデルの構築
5. モデルの評価
6. 予測の実行

上記の手順をコードに落とし込んだものが以下となります。

※このコードだけではyour_data.csvがないので正しく動作しませんが、コードにすると分かりやすいので載せておきます。

from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler

# データの読み込み（例）
df = pd.read_csv('your_data.csv')

# 前処理の例（欠損値の処理、データの標準化など）
df = df.dropna()  # 欠損値の削除

# データの分割
X = df[['study_hours', 'sleep_hours']]
y = df['test_score']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# データの標準化
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)

# モデルの構築と学習
model = LinearRegression()
model.fit(X_train_scaled, y_train)

# テストデータでの予測と評価
y_pred = model.predict(X_test_scaled)
r2 = r2_score(y_test, y_pred)
mse = mean_squared_error(y_test, y_pred)

print(f"テストデータでの決定係数（R²）: {r2:.4f}")
print(f"テストデータでの平均二乗誤差（MSE）: {mse:.4f}")

まとめ

回帰分析は、データ間の関係性を数式で表現し、将来の予測を可能にする強力な統計手法です。

Pythonを使えば簡単に回帰分析を実行でき、データから有益な洞察を得ることができます。

初めは単回帰分析から始めて、徐々に重回帰分析などの複雑な手法に挑戦してみるとよいでしょう。

最後に覚えておきたいのは、回帰分析はあくまで予測のツールであり、100%正確な結果を保証するものではないということ。

データの質や量、モデルの選択によって精度は変わってきます。

実際にPythonで様々なデータを分析してみることで、回帰分析の理解がさらに深まるでしょう。